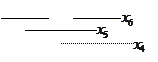Этот метод наиболее удобен для решения инженерных задач, т.к. позволяет упростить поиск склеивающихся членов, но он ограничен числом аргументов данной функции. Практически минимизация по методу карт Вейча производится для функций с числом аргументов не более восьми 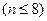 .
.
Карта Вейча представляет собою специальную таблицу функции.
Рассмотрим карту для функции 2-х переменных.

Можно упростить карту, если для аргументов ввести символические обозначения черточкой, поставив ее там, где они равны единице.
В карту вносятся значения функции, соответ-ствующие наборам переменных.
Расположение клеток таблицы легко определить склеивающиеся члены. Соседние клетки соответствуют членам, отличающимся одним знаком, и их можно склеивать, если значение функции в них равно единице.
Записав члены СДНФ функции в соответствующих клетках, можно легко увидеть. Например, в приведенной выше карте.
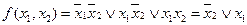
Члены столбца склеиваются той переменной, которой соответствует весь столбец, а строки – вся строка.
Рассмотрим карту Вейча для функции 3-х переменных. Карту будем строить с симметричным расположением аргументов, один из них расположим с одной стороны, два других – с другой.
Разделим карту двумя осями, симметрично которым и будем располагать аргументы (см. карту).
Каждая клетка карты соответствует членам СДНФ функции, содержащим 3 знака.
Обратите внимание, что каждая пара соседних клеток может быть склеена, могут быть склеены любые четыре соседние клетки и все восемь.
Так можно склеить клетки 1 и 5, 1 и 2 и т.д., а также 2, 3, 6, 7; 1, 5, 4, 8 и т.д.
Если представить карту свернутой по вертикали в цилиндр, то крайние клетки окажутся рядом, их тоже можно склеить.
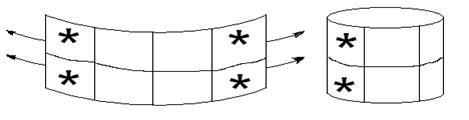
Рассмотрим несколько примеров
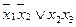
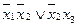
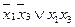
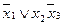

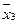
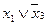
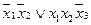 нельзя склеить
нельзя склеить
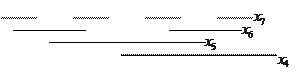
Приведем примеры карт Вейча для числа аргументов

Размещение аргументов в карте Вейча может быть произвольным. Лучше располагать половину их на одной стороне другую половину на другой. Более удобен вариант с симметричным, относительно центральных осей, расположением аргументов.
Возможен и другой способ, при котором значение аргументов располагается справа в пределах полукарты, четверть карты и т.д.
Чтобы упростить отыскание нужной клетки в карте Вейча, целесообразно дополнительно пронумеровать строки и столбцы.

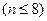 .
.



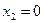


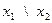
 1
1
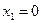
 1
1
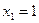
 1
1
 1
1







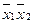

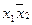
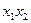

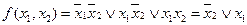

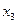





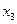

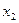
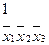
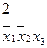
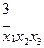
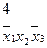

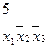
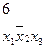

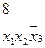



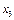

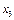

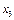

















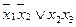
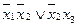
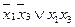

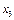

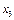

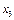


















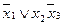

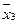

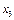

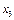

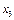















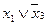
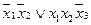 нельзя склеить
нельзя склеить