Нахождение всех возможных тупиковых форм

Не находя существенных импликант, обозначим все простые импликанты латинскими буквами. Исходная функция может быть записана в виде дизъюнкции простых импликант, что соответствует сокращенной форме (которая является единственной). Эта форма является также тупиковой. Для отыскания всего множества тупиковых форм запишем тождественную логическую формулу:

где - простые импликанты, соответствующие меткам -го столбца, - количество меток в -м столбце, - количество столбцов в таблице меток. Формула дает полную совершенную нормальную дизъюнктивную форму функции, т.е. .

Если в формуле встретятся члены и 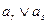, то член 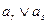можно не писать, ибо 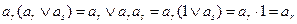(вот почему на 3 этапе метода Квайна выброшены большие столбцы).

Выражение необходимо упростить (раскрыть скобки и применить законы алгебры логики). Получим дизъюнкцию членов, каждый из которых дает множество простых импликант, входящих в тупиковую форму. Составим таблицу.

№№	Тупиковые формы	Общее число букв в тупиковой форме	Число членов в тупиковой форме
1.
2.
3.
.
.

Тупиковые формы с наименьшим числом букв и есть минимальные формы, тупиковые формы с наименьшим числом членов есть кратчайшие формы. Чаще всего минимальная форма не совпадает с кратчайшей.

Рассмотрим на примере 5 этот метод (см. таблицу этапа 2 в методе Квайна). Начертим ее здесь. Обозначив первичные импликанты латинскими буквами a, b, c, d, e, f, а столбцы цифрами (1), (2), …, (8).

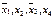
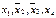
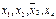
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
	a	V			V
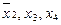
	b	V					V
	c			V	V
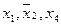
	d					V	V
	e					V			V
	f		V	V				V	V

Составим функцию .

Дизъюнкция 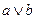включается для реализации меток 1-го столбца и т.д. По закону поглощения , поэтому члены 3 и 8 можно не записывать. Упростим .

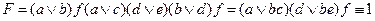
Раскроем скобки

Каждый из членов дает тупиковую форму данной функции. Составим таблицу.

№№	Тупиковые формы	Общее число букв в тупиковой форме	Число членов в тупиковой форме
1.		3+3+2=8
2.		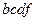3+3+3+2=11
3.		3+3+3+2=11
4.		3+3+3+2=11

Из таблицы следует, что 1-е решение есть минимальная форма (сравните результат), оно же дает кратчайшую форму. Отметим еще раз, что кратчайшая и минимальные формы могут не совпадать.

Итак, 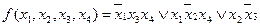есть минимальная форма данной функции.

Замечание 3. Таблица покрытий может не содержать существенных импликаций. Поясним, как в этом случае поступить. Пусть таблица меток имеет вид: (см. ниже).

Исключим 2 и 7 столбцы, т.к. 3 и 5 являются их частями, а из оставшихся столбцов выбираем столбец с наименьшим числом меток. Здесь во всех столбцах их по 2, поэтому возьмем 1-й столбец. Примем за псевдосущественную импликанту , а затем .

		2					7
a	v	v	v				v
b		v	v	v		v
c		v		v	v		v
d	v				v	v	v

Рассмотрим 2 частных случая:

1)

1

2)

a

v

v

a

v

v

a

v

v

b

v

v

v

b

v

v

v

b

v

v

v

c

v

v

c

v

v

c

v

v

d

v

v

v

d

v

v

v

d

v

v

v

Исключим большие столбцы, содержащие в себе выбранные псевдостолбцы. Запишем множество тупиковых форм для каждой таблицы. Это можно сделать по методу Патрика, но здесь можно перебрать все возможные варианты по таблице

1):		(1)	2):		(4)
		(2)			(5)
		(3)

Рассмотрим совместно множества решений. Решение (2) входит в (5), (3) совпадает с (4), а (1) нет соответствующего во 2-й таблице, наиболее простая тупиковая форма (5). Таким образом, разбиение на подтаблицы упрощает отыскание тупиковых форм.