Выбор методов оптимизации

В соответствии с указанной в предыдущем разделе возможностью разделения поставленной трёхмерной задачи на 3 одномерных, целесообразно применить для её решения однофакторные методы, приведенные в левой части рисунка. Рассмотрим их особенности.

3.2.4.1 Метод перебора

Суть метода заключается в том, что на факторное пространство, в котором производится поиск оптимума, накладывается сетка с заданным шагом, определяются значения критерия оптимизации в каждом из узлов сетки и оптимальным сочетанием значений факторов считаются координаты узла, давшего наилучшее значение критерия.

Благодаря такому подходу риск пропустить оптимум значительно меньше, чем при использовании методов половинного деления и золотого сечения, причем вероятность такого события можно регулировать, уменьшая шаг сетки. И в этом состоит основное достоинство метода.

Недостатком является большое количество процедур определения числовых значений критериев оптимизации. В рассматриваемой задаче факторное пространство является трёхмерным (продольная, поперечная и вертикальная координаты помещения). Если рассмотреть заданный вариант габаритов помещения (L=42м; B=20м; H=12м), то нетрудно подсчитать, что для шага сетки по всем координатам Δ=0,1м (в соответствии с заданной точностью) общее число узлов сетки (а следовательно, и количество определений соответствующих значений критериев оптимизации) будет равно:

N = 421×201×121 = 10 239 141

Понятно, что для экспериментальной оптимизации с использованием натурных объектов или их физических моделей такой способ совершенно неприемлем.

Однако в данной задаче речь идет о математическом эксперименте. Учитывая быстродействие современных ПЭВМ, в принципе можно организовать эти вычисления с помощью достаточно несложной программы. Определённые технические трудности с выделением необходимого объема памяти могут возникнуть при попытке сохранения всего массива данных для последующего анализа. Однако для решения именно оптимизационной задачи нет необходимости разделять оптимизацию на 2 этапа: формирование массива и поиск наилучшего узла. Эти процедуры вполне можно совместить, если выделить две ячейки памяти (для хранения номера узла и соответствующего значения критерия) и обновлять их содержимое всякий раз, когда вычисленное значение критерия окажется лучшим, чем предыдущего.

Тем не менее, этот алгоритм можно упростить, воспользовавшись указанной ранее возможностью раздельной оптимизации по каждой из координат, т.е. сведением трехмерной задачи к трём одномерным:

Одномерная оптимизация методом перебора

При этом упрощаются формулы для определения критериев. Например, при оптимизации по критерию К₁ (суммарная длина коммуникаций) можно применить выражения:

В результате резко уменьшается и количество вычислений. Нетрудно подсчитать для приведенного выше примера общее количество шагов:

N₁ = 421 + 201 + 121 = 743

Тем не менее, движение к оптимуму можно еще ускорить, если применить специальные методы, предусматривающие минимизацию числа процедур при поиске оптимума.

3.2.4.2 Метод половинного деления

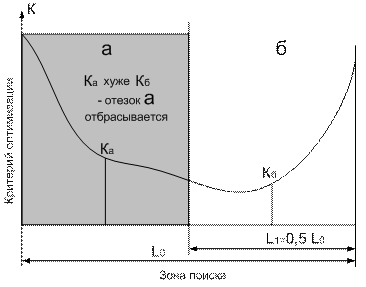
Идея метода заключается в том, что оптимизация выполняется рядом последовательных дискретных этапов:

- в каждой из половин определяют среднюю точку и вычисляют или экспериментально определяют для этих точек значения критерия оптимизации;

- ту половину, в середине которой значение критерия оказалось хуже, отбрасывают, уменьшая, таким образом, ширину зоны поиска в 2 раза:

Эти процедуры повторяют до тех пор, пока ширина зоны поиска не станет меньше заданной точности оптимизации.

Для заданного примера поиск оптимума методом половинного деления с точностью до 0,1 м. потребовал 10 шагов в продольном направлении, 8 шагов в поперечном направлении и 7 шагов в вертикальном направлении, т.е. всего 25 шагов для одного критерия. Для оптимизации по всем трём критериям потребуется 75 шагов:

Номер шага	Поиск по оси X	Поиск по оси Y	Поиск по оси Z
	10,5
	5,25	2,5	1,5
	3,62	1,25	0,75
	1,81	0,6	0,38
	0,91	0,3	0,19
	0,45	0,15	0,1
	0,23	0,08
	0,12
	0,06

Преимуществом метода является очень быстрое приближение к оптимуму, поскольку уменьшение ширины зоны поиска определяется степенной функцией 2ⁿ, где n – число шагов.

Недостатком метода является возможность сбоя при наличии в зоне поиска нескольких минимумов (или максимумов) критерия. В этом случае метод не гарантирует выход на самый меньший из минимумов (или самый больший из максимумов).

3.2.4.3 Метод золотого сечения

Оптимизация этим методом также выполняется рядом последовательных дискретных этапов, на каждом из которых происходит уменьшение ширины зоны поиска. Отличие от предыдущего метода состоит в том, что зона поиска на каждом из этапов делится не пополам, а в пропорции «золотого сечения» (если ширину зоны принять за 1, то отрезки примерно 0,618 и 0,382).

Итальянским учёным Фибоначчи было доказано, что именно такой способ деления диапазона поиска обеспечивает самый быстрый выход к оптимуму. В этом состоит преимущество данного метода.

Недостаток метода золотого сечения тот же, что и у метода половинного деления – отсутствие гарантии выхода на абсолютный оптимум при сложном характере целевой функции. Кроме того, алгоритм вычисления координат при пошаговом сокращении диапазона методом золотого сечения несколько сложнее, чем при половинном делении, поскольку при каждом шаге нужно случайным образом задавать, какой из отрезков (правый или левый) будет большим.

В целом, анализ рассмотренных методов оптимизации, в основе которых лежит пошаговое сокращение зоны поиска оптимума, позволяет сделать вывод: присущая им высокая скорость приближения к оптимуму делает их применение особенно эффективным в тех исследованиях, где очень важно сведение до минимума числа шагов. Например, при проведении дорогостоящей и трудоёмкой экспериментальной оптимизации с использованием натурных объектов, сложных стендовых установок, расходованием топлива и т.п.

Применению их должен предшествовать предварительный анализ возможного характера целевой функции для сведения к минимуму риска пропуска истинного оптимума.

3.2.4.4 Аналитический метод оптимизации

Классический способ аналитической оптимизации в пространстве одного параметра X предусматривает поиск координат экстремума (максимума или минимума) целевой функции K=f(X) путем её дифференцирования и решения уравнений:

при , если отыскивается координата минимума критерия или при , если отыскивается координата максимума.

Если решение даёт одно значение на всём диапазоне варьирования параметра X – оно и считается оптимальным. Если решений несколько – выбирается наименьший минимум или наибольший максимум.

При отсутствии экстремумов внутри диапазона варьирования параметра X вычисляют значение критерия на границах диапазона и считают оптимальным то граничное значение параметра X, которое даёт наилучший результат. Разумеется, применить этот метод можно только для дифференцируемых функций (т.е. непрерывных и гладких на всём диапазоне варьирования параметра X).

Для рассматриваемого примера это условие не соблюдается, поскольку зависимости значений критериев от положения распределителя описываются кусочно-линейными функциями, имеющими перегибы при совпадении координаты распределителя с координатами потребителей.

Линейный характер объясняется принятыми допущениями об отсутствии петель и криволинейных участков коммуникаций, а также неизменностью удельных характеристик каждой из трасс на всём её протяжении.

Перегибы объясняются тем, что при переходе распределителя мимо очередного потребителя, изменение расстояния от распределителя до этого потребителя меняет свой знак: при подходе распределителя к потребителю расстояние уменьшается, а при движении распределителя за потребителем оно увеличивается.

Дифференцировать такую целевую функцию нельзя, однако для поиска оптимума можно использовать следующее соображение: для кусочно-линейной функции минимум критерия должен совпадать с одной из точек перегиба, т.е. оптимальная координата распределителя должна совпадать с координатой одного из потребителей.

Следовательно, для оптимизации расположения распределителя, например, в продольном направлении, достаточно поочередно совместить положение распределителя X_Р c координатой каждого из потребителей X_Пi, вычислить для каждого шага значение критерия и выбрать ту точку, которая обеспечивает наилучшее значение критерия.

При этом для заданного примера с числом потребителей n = 9 число шагов N = 3·n =27.

Если оптимизация по разным критериям даст различные результаты, окончательное решение о месте установки распределителя следует выполнить с учетом сравнительной важности критериев, для оценки которой может быть применен, например, метод экспертных оценок

Вывод: при правильном методическом подходе к решению, на первый взгляд, достаточно сложной многомерной задачи, можно существенно упростить алгоритм оптимизации без ущерба для точности.