Регрессионный анализ. Слово регрессия буквально означает «убывание»

Слово регрессия буквально означает «убывание». Целью регрессии является определение численных значений коэффициентов функциональной зависимости и последующая оценка значимости отдельных компонентов математической модели путём расстановки их в порядке убывания коэффициентов.

Так же, как и корреляционный анализ, регрессионный анализ может быть парным и множественным. Парный регрессионный анализ называется аппроксимацией.

Наиболее распространённым способом аппроксимации является метод наименьших квадратов. Название обусловлено тем, что значения коэффициентов определяют из условия минимального значения среднеквадратической ошибки аппроксимации.

Основные этапы метода:

· Записывают в алгебраическом виде функциональную взаимосвязь параметров (она может быть известна заранее, или определена при проведении корреляционного анализа, либо просто выбрана из библиотеки типовых функций). Допустим, она имеет вид:

Y = B₀+B₁X+B₂X²

· Записывают среднеквадратическую ошибку аппроксимации: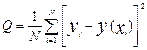

где y_i – заданные табличные значения параметра y;

y(x_i) – значения параметра y, определённые в алгебраическом виде с помощью выбранной функции для заданных табличных значений параметра x.

· Находят численные значения коэффициентов регрессии В₀, В₁ и В₂, при которых среднеквадратическая ошибка Q будет иметь минимальное значение. Для этого приравнивают 0 частные производные

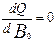
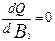
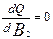и решают полученную систему уравнений относительно коэффициентов В₀, В₁ и В₂

• Оценивают точность аппроксимации с помощью максимальной и среднеквадратичной погрешностей.

Если алгебраический вид аппроксимирующей функции заранее не задан, придётся применить этот метод поочерёдно ко всем функциям, хранящимся в библиотеке типовых функций, и затем выбрать ту из них, которая обеспечит минимальные погрешности аппроксимации. Разумеется, эти действия реализуются с помощью специальных компьютерных программ.

В результате аппроксимации табличная форма задания параметров преобразуется в аналитическую форму, гораздо более удобную для вычисления промежуточных значений параметров и для включения в компьютерные программы.