 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Модель второго порядка
|
|
Для объектов, функционирование которых может содержать такие процессы и взаимодействия, часто удаётся получить адекватную модель с помощью полинома второго порядка. Если обозначить k - количество факторов, то такая модель в общем виде будет выглядеть следующим образом:

| |||
| Отклик | Линейная часть модели | Эффекты взаимодействия факторов | Квадратичные члены |
Для рассматриваемого в лабораторной работе объекта, имеющего три изменяемых в процессе эксперимента параметра (фактора) k=3 и квадратичная модель в развёрнутом виде может быть записана следующим образом:
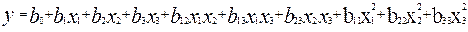 Модель содержит 10 неизвестных коэффициентов bi, подлежащих определению экспериментальным путём. Для произвольного числа факторов k число коэффициентов такой модели вычисляется следующим образом:
Модель содержит 10 неизвестных коэффициентов bi, подлежащих определению экспериментальным путём. Для произвольного числа факторов k число коэффициентов такой модели вычисляется следующим образом:

| Число факторов k | |||||
| Число коэффициентов l |
Выбор типа плана
Для определения численных значений коэффициентов квадратичной модели необходим план эксперимента, предусматривающий варьирование каждого из факторов не менее, чем на трёх уровнях (два уровня соответствуют двум изученным точкам факторного пространства, которые однозначно определяют только линейные функции, но для квадратичных функций не дают определённого решения, поскольку через две точки можно провести бесчисленное множество парабол).
Однако, планы полного факторного эксперимента с тремя уровнями варьирования (ПФЭ 3k) предусматривают слишком большое число опытов:
| N=3k | Число факторов k | ||||
| Число опытов N |
Для определения численных значений коэффициентов квадратичной модели целесообразно применять планы, которые получаются путем достраивания планов полного (при k ≤ 5) или дробного (при k > 5) экспериментов с двумя уровнями варьирования факторов.
Процедура достраивания заключается в том, что к указанному выше плану ПФЭ или ДФЭ, который называют «ядром», добавляют опыт в центре эксперимента и, так называемые, «звездные точки». Они расположены на осях координат и отстоят от начала координат на расстоянии α, которое называется «звёздным плечом».
| Графическое представление ЦКП для объекта с двумя варьируемыми факторами. | 
|
Полученный таким образом план называют центрально-композицион-ным планом (ЦКП). Центральным потому, что он симметричен относительно центра эксперимента, а композиционным потому, что он получен последовательным достраиванием.
Поскольку в таком плане число уровней больше двух, кодированные значения факторов уже нельзя записывать просто в виде «-» и «+».
Матрица и графическое представление ЦКП для двух факторов:
| № | X0 | X1 | X2 | X1·X2 | 
| 
| Части ЦКП |
| +1 | +1 | +1 | +1 | +1 | +1 | Ядро Nя = 2k | |
| +1 | -1 | +1 | -1 | +1 | +1 | ||
| +1 | +1 | -1 | -1 | +1 | +1 | ||
| +1 | -1 | -1 | +1 | +1 | +1 | ||
| +1 | +α | α2 | Звёздные точки N* = 2k | ||||
| +1 | -α | α2 | |||||
| +1 | +α | α2 | |||||
| +1 | -α | α2 | |||||
| +1 | Центр |

Матрица ЦКП для трёх факторов:
| № | X0 | X1 | X2 | X3 | X1·X2 | X1·X3 | X2·X3 | 
| 
| 
| Части ЦКП |
| +1 | -1 | -1 | -1 | +1 | +1 | +1 | +1 | +1 | +1 | Ядро Nя = 2k | |
| +1 | +1 | -1 | +1 | -1 | +1 | -1 | +1 | +1 | +1 | ||
| +1 | -1 | +1 | +1 | -1 | -1 | +1 | +1 | +1 | +1 | ||
| +1 | +1 | +1 | -1 | +1 | -1 | -1 | +1 | +1 | +1 | ||
| +1 | -1 | +1 | -1 | -1 | +1 | -1 | +1 | +1 | +1 | ||
| +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | ||
| +1 | -1 | -1 | +1 | +1 | -1 | -1 | +1 | +1 | +1 | ||
| +1 | +1 | -1 | -1 | -1 | -1 | +1 | +1 | +1 | +1 | ||
| +1 | +α | α2 | Звёздные точки N* = 2k | ||||||||
| +1 | -α | α2 | |||||||||
| +1 | +α | α2 | |||||||||
| +1 | -α | α2 | |||||||||
| +1 | +α | α2 | |||||||||
| +1 | -α | α2 | |||||||||
| +1 | Центр |
Кодированные значения факторов, приведённые в таблицах, определённые в соответствии с формулой:

где 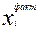 - фактическое значение i-го фактора в данном опыте;
- фактическое значение i-го фактора в данном опыте;
 - фактическое значение i-го фактора в центре эксперимента:
- фактическое значение i-го фактора в центре эксперимента:
 - интервал варьирования i-го фактора.
- интервал варьирования i-го фактора.
Количество опытов ЦКП определяется соотношением:
Nцкп = Nя + N* + N0 = 2k + 2k + 1
Сравнение количества опытов полного факторного эксперимента на трёх уровнях и ЦКП приведено в таблице:
| Число факторов k | ||||
| Число опытов ПФЭ типа 3k | ||||
| Число опытов ЦКП |
Данные, приведённые в таблице, указывают на то, что при числе факторов k > 2 применение ЦКП позволяет существенно сократить число опытов по сравнению с планами полного факторного эксперимента на трёх уровнях.
Уровни варьирования для каждого фактора:
-α, -1, 0, +1, +α - итого 5 уровней.
Таким образом, ЦКП, по сравнению с ПФЭ типа 3k, обеспечивает большее число уровней варьирования при меньшем числе опытов, чем и определяется его преимущество. Первый символ пароля компьютерного теста «7».
Дата публикования: 2014-11-18; Прочитано: 1298 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
