Классические модели в виде дифференциальных уравнений

Дифференциальные уравнения описывают процесс перехода динамической системы из одного состояния в другое и изменение выходного параметра. Могут рассматриваться системы, в которых моделируют только изменение состояний или только изменение выходного параметра. Могут рассматриваться системы, в которых моделируют изменение и состояний, и выходного параметра. Математические схемы такого вида отражают динамику изучаемой системы и носят название D-схем от английского слова dynamic (динамика).

Пусть входные параметры (сигналы, координаты и прочее) заданы множеством Х(t)={х₁(t),х₂(t),...,х_m(t)}, а выходные параметры заданы множеством Y(t)={y₁(t),y₂(t),..., y_r(t)}. Модель динамической системы, определяемая обыкновенными дифференциальными уравнениями в общем виде, задается следующим образом.

Задают дифференциальные уравнения, определяющие движение системы в пространстве состояний

. (2.6)

Каждое i -е дифференциальное уравнение задается в общем виде функцией f_i, зависящей от времени t, компонент вектора состояний Z={z₁(t),z₂(t),…,z_n(t)} и компонент вектора входных параметров Х(t)={х₁(t),х₂(t),...,х_m(t)}. Задают соотношения, определяющие изменение выходных параметров

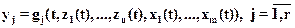. (2.7)

Для решения дифференциальных уравнений системы (2.6), определения изменения во времени выходных параметров необходимо для момента t(0)=t₀ задать начальные состояния ,

а также функции, определяющие изменения во времени компонент вектора входных параметров Х(t) на полуинтервале (t₀,t]:

.

Если для каждого уравнения системы (2.6) выполнены условия существования и единственности решений, то эти решения в общем случае имеют вид

. (2.8)

Обозначим решения системы дифференциальных уравнений (2.6), проходящие в момент времени t₀ через точку , символом F. Тогда модель в виде функции переходов для динамической системы будет задана в общем виде уравнением

. (2.9)

Эта функция каждому набору ставит в соответствие то состояние Z(t), в которое переходит система за время перехода t-t₀ из фазы (t₀,Z₀) под действием входных параметров .

Модель динамической системы в виде функции выходов в общем виде будет определена уравнением

(2.10)

в котором оператор G каждому набору сопоставляет выходной сигнал y_t=y(t).

Дифференциальные уравнения классифицируются на линейные и нелинейные, стационарные и нестационарные, уравнения первого и более высокого порядка, а также одномерные и многомерные.

Если модель предназначена для описания изменения состояния z(t) динамической системы, то модель в виде обыкновенного линейного дифференциального уравнения q- го порядка с постоянными коэффициентами и правой частью, выраженной через производные от управляющих функций, задается в следующем виде:

(2.11)

Если применить оператор дифференцирования , то с учетом аддитивной ошибки v(t) уравнение (2.11) запишется в виде

z(р)=l^-1(р)m(р)х(р)+v(р),

где l^-1(р)=р^q-l₁р^q-1-l₂р^q-2-…-l_q, m(р)=m₀р^r+m₁р^r-1 + … + m_r.

Модели в виде многомерных дифференциальных уравнений в форме Коши находят наибольшее применение. Они описываются системами обыкновенных дифференциальных уравнений первого порядка в форме Коши, т.е. разрешенными относительно первых производных. Для стационарной линейной системы, параметры которой изменяются непрерывно во времени, модель в общей форме имеет следующий вид:

. (2.12)

В уравнении (2.12): Z={z₁(t),z₂(t),…,z_n(t)} - вектор состояний; Х(t)={х₁(t),х₂(t),...,х_m(t)} – вектор входных параметров; Y(t)={y₁(t),y₂(t),..., y_r(t)} – вектор выходных параметров; W={w₁(t),w₂(t),…,w_n(t)} - вектор шума системы; - транспонированный вектор производных от переменных состояния; матрицы Ф, G, H и Г имеют размерности, зависящие от размерностей векторов Z, Х(t), Y(t), W. Коэффициенты матриц Ф, G, H и Г имеют смысл коэффициентов передачи, для стационарной системы не зависят от времени и подлежат оцениванию. Параметры могут входить и в начальное условие, которое необходимо добавить для решения первого уравнения (2.12).

Модель для нестационарной линейной непрерывной системы отличается от (2.12) тем, что матрицы Ф, G, H и Г будут зависеть от времени.

Непрерывная нелинейная система может быть описана моделью

(2.13)

Векторные функций j(…), y(…) и матрица Г(...) предполагаются известными с точностью до параметров, подлежащих оцениванию. Применяя преобразования Лапласа, можно перенести описание из временной области в область изображений по Лапласу.

Компьютерное моделирование систем, описываемых многомерными дифференциальными уравнениями в форме Коши, осуществляется с применением пакетов программ. Широко используется подсистема Simulink пакета MatLab. При моделировании определяется вид дифференциального уравнения, задаются начальные условия. Результаты решения отображаются визуально в виде цифровых данных, а также в виде графических данных.