Примеры моделей в виде дифференциальных уравнений

2.1.1. Модель электрического колебательного контура. Классические разделы высшей математики связаны с решением и исследованием дифференциальных уравнений. Дифференциальные уравнения нашли широкое применение при моделировании технических, социальных, экономических и других систем.

Классическая теория автоматического управления применяет модели объектов в виде дифференциальных уравнений и позволяет решать задачи управления, исследуя дифференциальные уравнения [5]. Вид уравнений может быть очень сложным и для решения и исследования моделей, заданных дифференциальными уравнениями, применяется компьютерное моделирование. Применяют специальные пакеты прикладных программ, например MatLab, Omola, Dymola, Dymosim, Model Vision Studium, язык UML и другие.

Колебательный контур, известный в электротехнике, представляют в виде схемы, приведенной на рис. 2.1. Определены параметры колебательного контура:

- С – емкость конденсатора;

- L – индуктивность катушки;

- U_С(t) – напряжение на конденсаторе;

- I_L(t) – ток в катушке;

- U(t)_ИСТ – напряжение внешнего источника.

Определим модель колебательного контура, которая позволит моделировать колебательный процесс в контуре.

Рис. 2.1

В соответствии с законом Кирхгофа запишем следующие соотношения:

, .

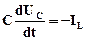Введем координаты z₁=U_С, обозначим U_ИСТ/L=х(t) и получим систему дифференциальных уравнений:

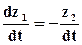, _. (2.1)

Если U_ИСТ =0, то х(t) =0 и система (2.1) описывает свободные колебания. Рассматривая х(t) как сигнал управления, получим описание динамики колебаний в каждый момент времени t. Решая систему (2.1), можно получить аналитический вид функций z₁(t) и z₂(t).

Если рассматривать U(t)_ИСТ как единичное ступенчатое воздействие, R - внутреннее сопротивление источника, то можно показать, что напряжение на конденсаторе С будет изменяться по формуле [6]:

, (2.2)

где , , .

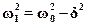Дальнейшее исследование модели связано с разработкой программы, которая будет рассчитывать и выводить график функции U_С(t) в зависимости от параметров R, L и С, тем самым позволяя исследовать время переходного процесса (время затухания колебаний) в данном контуре.

2.1.2. Модель размножения микроорганизмов. Из результатов изучения развития популяций микроорганизмов известно, что скорость размножения микроорганизмов пропорциональна числу уже имеющихся на данное время. Рассмотрим моделирование процесса роста популяций микроорганизмов.

Пусть E(t) - число особей в момент времени t. Скорость размножения определим как отношение величины E(t+∆t)-E(t) к величине Dt при Dt®0. Исходя из этого условия, получим уравнение в частных приращениях (модель роста популяций в частных приращениях):

Переходим к предельному выражению

и получаем модель роста популяций микроорганизмов в виде дифференциального уравнения (общий вид):

. (2.3)

Решая дифференциальное уравнение (2.3), можно получить аналитическое уравнение роста популяций и провести исследования. При начальных условиях t=0, E(t=0)=E₀ получим решение модели роста популяций в виде аналитического выражения

E(t)=E₀e^kt. (2.4)

Вид уравнения (2.4) показан на рис. 2.2.

Рис. 2.2

Если при t=0 начальное число популяций микроорганизмов E=E₀, то можно определить время Т, за которое число особей удвоится по формуле

2E₀=E₀e^kt, ® 2=e^kT, ® T=(1/k)ln2.

Заметим, что при получении этой модели не учитывалось ограничение, связанное с требуемым количеством питательных средств для существования микроорганизмов, а также воздействия внешней среды (например, иммунные силы организма).

2.1.3. Модель динамики боя. Проведение военных сражений связано с расчетами, поэтому разрабатывают модели боевых действий [2].

Пусть m₁ - число боевых единиц красных; m₂ - число боевых единиц синих, сохранившихся непораженными к моменту времени t; λ₁ - средняя скорострельность для одной боевой единицы красных; λ₂ - средняя скорострельность для одной боевой единицы синих. Цели поражаются с вероятностью р₁ - красными и вероятностью р₂ - синими. Рассмотрим модель, отображающую динамику боя.

Интенсивности успешных выстрелов определятся как

L₁=λ₁р₁, L₂=λ₂р₂.

Число выведенных боевых единиц красных Dm₁ за время Dt составит λ₂р₂Dtm₂, а число выведенных из строя боевых единиц синих Dm₂ за время Dt составит λ₁р₁Dtm₁, Тогда

Dm₁=-λ₂р₂Dtm₂, Dm₂=-λ₁р₁Dtm₁. (2.4)

Уравнения (2.4) - модель динамики боя в частных приращениях. От уравнения (2.4) осуществим переход к дифференциальным уравнениям.

Разделив правую и левую части на Dt, получим

, .

Взяв пределы при Dt®0, получим дифференциальные уравнения, моделирующие динамику боя

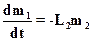_, (2.5)

Уравнения (2.5) называются уравнениями Ланчестера.

2.1.4. Модель движения ракеты. Движение ракеты, запускаемой в космос, описывается её координатами х и y, проекциями вектора скорости V на координатные оси V_Х и V_Y. Пусть m - масса ракеты; u величина тяги; j - угол между направлением тяги и осью 0х; f(u) - секундный расход массы. Рассмотрим построение модели, отображающей динамику полета.

Проекции скоростей являются производными от движения по координатам, следовательно

, .

В соответствии с уравнением Ньютона запишем:

.

Расход массы определится уравнением

.

Таким образом, моделью движения ракеты является система уравнений:

при начальных условиях х(t₀)=х₀, y(t₀)=y₀, m(t₀)=m₀, V_х(t₀)=V_х0, V_y(t₀)=V_y0.

Управление траекторией ракеты осуществляется за счет регулирования величины и направления силы тяги двигателя, U и j - управляющие параметры.

Во всех приведенных выше примерах применение компьютерного моделирования сводится к получению аналитических уравнений, программированию с целью получения решений при заданных наборах входных параметров, визуализации результатов решения.