 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Дизъюнктивные нормальные формы
|
|
I Важным примером эквивалентности является разложение булевой функции по переменной - представление функции
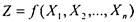 в виде
в виде
\
| Справедливость  этого тождества следует из того, что оба слагаемых, связанных знаком дизъюнкции, не могут одновременно равняться 1,|
этого тождества следует из того, что оба слагаемых, связанных знаком дизъюнкции, не могут одновременно равняться 1,|
•< i -:> ч - - - так как один из сомножителей X или X равняется 0. При подстановке
i,-- ' i -О в левую часть равенства константы 0 на место Х\ второе слагаемое в
правой части обращается в 0, а при подстановке константы 1 - первое.
(Функции (/1 — 1) переменных  имеют в качестве столбцов значений соответственно верхнюю и нижнюю половины столбца значений
имеют в качестве столбцов значений соответственно верхнюю и нижнюю половины столбца значений  I Например, функция
I Например, функция
 , имеющая столбец значений
, имеющая столбец значений 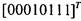 , при разложении
, при разложении
по первой переменной может быть представлена.
 , и поскольку
, и поскольку  - таблица для конъюнкции, а
- таблица для конъюнкции, а  - для дизъюнкции, то
- для дизъюнкции, то

В каждом из слагаемых функции от переменных 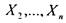 могут
могут
; быть таким же образом разложены по переменному  и т д.
и т д.
Примеры. 1) Для функции одной переменной  разложение
разложение
имеет вид  Обозначим
Обозначим 
Тогда  - константы, равные значениям
- константы, равные значениям
функции  j В этих обозначениях таблица функции
j В этих обозначениях таблица функции 
есть 
I 2) Для функции 3 переменных  разложение по
разложение по
переменной X даег
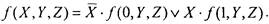
Далее, обозначая  - через
- через
 , разложим их по переменной Y:
, разложим их по переменной Y:
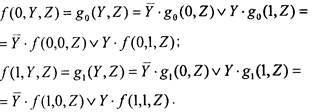
Тем самым, получаем разложение исходной функции на 4 логических слагаемых:  /
/
 [раскрывая скобки]
[раскрывая скобки]

Далее, вводя новые обозначения, 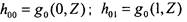
 , разложим эти 4 функции по их единственной переменной Z:
, разложим эти 4 функции по их единственной переменной Z:
i
Окончательно  подставляя эти выражения в предыдущую формулу и раскрывая скобки, получаем разложение
подставляя эти выражения в предыдущую формулу и раскрывая скобки, получаем разложение  по всем трем
по всем трем
переменным в виде дизъюнкции 8 логических слагаемых:
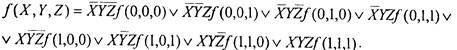
Каждое слагаемое представляет здесь конъюнкцию переменных и их отрицаний и некоторой константы, определяемой значением
' функции 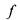 на определенном наборе своих переменных, причем -переменная входит в конъюнкцию с отрицанием только, если ее значение в этом наборе равно 0. В связи с этим введем понятие: [ Элементарная конъюнкция - конъюнкция нескольких I переменных и их отрицаний, в которую каждая переменная входит не
на определенном наборе своих переменных, причем -переменная входит в конъюнкцию с отрицанием только, если ее значение в этом наборе равно 0. В связи с этим введем понятие: [ Элементарная конъюнкция - конъюнкция нескольких I переменных и их отрицаний, в которую каждая переменная входит не
! более одного раза.(Примеры элементарных конъюнкций:  [
[  . Формулы
. Формулы 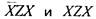 не являются элементарными
не являются элементарными
[конъюнкциями: первая содержит одновременно переменную X и ее [отрицание, во вторую переменная X входит дважды. | I Для дальнейшего введем удобное обозначение: 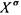 - форма
- форма
^записи функции 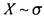 , где X - переменная, а
, где X - переменная, а 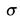 - двоичный
- двоичный
параметр.! Рассмотрим подробнее:/если подставить константу вместо
обеих переменных, получим равенства  ;
;
подстановка констант вместо X дает:  ; наконец, при
; наконец, при
подстановке констант вместо  получаем
получаем  . |
. |
Приведенные выше примеры элементарных конъюнкций можно в новых обозначениях записать так:
 и т.п. элементарная конъюнкция, соответствующая набору
и т.п. элементарная конъюнкция, соответствующая набору
=  - конъюнкция
- конъюнкция  . Для п -мерного
. Для п -мерного
набора конъюнкция содержит ровно п множителей с отрицаниями или
i без них. Как функция п переменных она принимает значение 1 только на наборе 
Используя введенные обозначения, можно записать предыдущее
i разложение функции  по-другому:
по-другому:
I
\  Теперь можно удалить из этой логической суммы те слагаемые, для
Теперь можно удалить из этой логической суммы те слагаемые, для
которых  (пользуясь свойствами 16 и 15). Логическую
(пользуясь свойствами 16 и 15). Логическую
сумму оставшихся членов можно записать так:
 или
или  короче:
короче: 
Имеется в виду, что в логической сумме участвуют только те элементарные конъюнкции, которые соответствуют наборам констант
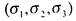 , для которых
, для которых 
Подобное представление возможно для любой булевой функции, и мы приходим к важному понятию, j
\ Совершенная дизъюнктивная нормальная форма (СДНФ) -
представление функции  в виде дизъюнкции всех
в виде дизъюнкции всех
элементарных конъюнкций, соответствующих наборам значений  , на которых Z = 1:
, на которых Z = 1:

СДНФ содержит ровно столько п -членных элементарных конъюнкций, сколько единиц в столбце значений функции
 . На каждом из
. На каждом из  наборов либо все логические слагаемые СДНФ обращаются в 0 (если функция
наборов либо все логические слагаемые СДНФ обращаются в 0 (если функция  на этом наборе
на этом наборе
равна 0), либо ровно одна конъюнкция обращается в 1 (если 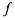 равна 1) Не имеет СДНФ единственная функция - тождественно равная нулю
равна 1) Не имеет СДНФ единственная функция - тождественно равная нулю
(константа 0).
Отсюда - простой способ выражения любой функции (кроме константы 0), заданной таблично, в виде СДНФ. По таблице значений составляются соответствующие элементарные конъюнкции и связываются знаком дизъюнкции.
Примеры. 1) Выражения 
 суть СДНФ этих
суть СДНФ этих
функций, а  не СДНФ..
не СДНФ..
2) СДНФ для функции большинства  содержит 4
содержит 4
элементарные конъюнкции: 
3) СДНФ для функции 4 переменных 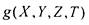 со столбцом
со столбцом
значений  содержит 6 элементарных конъюнкций:
содержит 6 элементарных конъюнкций:

Совершенная дизъюнктивная нормальная форма является частным случаем более общего вида формул.
\ Дизъюнктивная нормальная форма (ДНФ) -дизъюнкция нескольких элементарных конъюнкций. Подчеркнем, что ДНФ - это не всякая формула, выражающая функцию через операции конъюнкции,
дизъюнкции и отрицания например,  - не ДНФ, однако ее
- не ДНФ, однако ее
можно привести к ДНФ, раскрывая скобки: 
Используя некоторые из эквивалентностей, прежде всего, 1-6, можно выносить за скобки общие множители, а применяя равенства 7-10, 13-18, а также приемы склеивания, упрощать формулы, поскольку, как уже отмечалось, в этих равенствах правые части короче левых.
Примеры. 1) Докажем тождество: 
 = [раскрываем скобки] =
= [раскрываем скобки] = 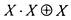 = [устраняем
= [устраняем
кратность] = 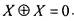
2) Докажем тождество:  > Преобразуем обе части равенства, выражая импликацию через
> Преобразуем обе части равенства, выражая импликацию через
'дизъюнкцию:  ; получаем:
; получаем:  = [снимаем
= [снимаем
двойное отрицание] = 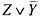 . Равенство доказано, поскольку
. Равенство доказано, поскольку
дизъюнкция - коммутативная операция.
I 3) Упростить формулу  . Выносим за скобки
. Выносим за скобки
[общий множитель
i 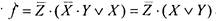
Дата публикования: 2014-11-18; Прочитано: 2272 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
