 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Логические формулы. Булева алгебра
|
|
"Задание функций непосредственно таблицей удобно лишь при небольшом числе переменных. Другим средством представления функций является суперпозиция, символическим (аналитическим) выражением которой служат формулы. Применение формул связано с использованием функциональных знаков - символов булевых функций. Некоторые из них уже встречались. Применение формул позволяет представить функции большого числа переменных суперпозициями
функций меньшего числа переменных, прежде всего через функции 1 и 2 переменных.
Формулы алгебры логики (пропозициональные формулы)
- формулы, построенные из знаков переменных и знаков функциональных операций с соблюдением определенных правил построения формул.
Поскольку мы будем рассматривать формулы, использующие исключительно одноместные и двуместные операции, приведем соответствующее индуктивное определение:
1) булевы константы 0, 1 - формулы;
2) переменные X,Y,Z и т.д. - формулы;
3) если F и G - формулы, то  - формулы, где
- формулы, где 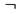 знак унарной операции (функции) отрицания, а
знак унарной операции (функции) отрицания, а  знак некоторой
знак некоторой
бинарной функциональной операции; F и G называются подформулами.
Согласно этому определению  формулы: переменные, связанные знаками функциональных операций
формулы: переменные, связанные знаками функциональных операций
 - также формулы, поскольку
- также формулы, поскольку  - формулы, и
- формулы, и
 суть функциональные знаки. Однако для сокращения формул принято использовать следующую иерархию (частичный порядок) функциональных символов. 'Знак
суть функциональные знаки. Однако для сокращения формул принято использовать следующую иерархию (частичный порядок) функциональных символов. 'Знак  связывает теснее знака
связывает теснее знака  , знак
, знак  - теснее знаков
- теснее знаков  , а последние - теснее знака равенства
, а последние - теснее знака равенства
=, связывающего равные формулы. Символически:

Кроме того, знак конъюнкции можно опускать подобно знаку умножения в алгебре; знак отрицания  , отнесенный к отдельной
, отнесенный к отдельной
переменной удобнее записывать как надстрочное отрицание  . Это соглашение, а также ассоциативность операций
. Это соглашение, а также ассоциативность операций  позволяют
позволяют
устранять излишние скобки, в том числе, внешние. Например, выражение

может быть записано короче: 
Формулам естественным образом соответствуют функции: знакам переменных - булевы переменные, а подформулам, соединенным функциональными знаками - булевы функции. При этом каждая формула
задает единственную функцию, но обратное не верно: для любой функции существует много различных представляющих ее формул. Например,
приведенное выше равенство  , предлагает две разные
, предлагает две разные
записи одной и той же функции. Другие примеры встречались при
определении функции  . Мы приходим к следующему понятию.
. Мы приходим к следующему понятию.
, Эквивалентные (равносильные) формулы -формулы, представляющие одну и ту же функцию.
Проверить равенство  двух булевых функций,
двух булевых функций,
представленных разными формулами, можно с помощью вычисления их значений на всех наборах значений переменных. Однако это трудоемкая процедура, и удобнее избрать другой путь: эквивалентные преобразования.
Прежде всего приведем равенства для формул, содержащих
операции конъюнкции, дизъюнкции и отрицания (X, Y,Z - логические переменные^.

! Конъюнкцию, дизъюнкцию и отрицание можно рассматривать как алгебраические операции над булевыми функциями. Свойства 1-2 выражают коммутативность, свойства 3-4 - ассоциативность^операций
 ; свойства 5-6 - взаимную дистрибутивность этих операций, что дает возможность раскрывать скобки в формулах. Свойства 7-8 -устранение кратности; свойства 9-10 называют правилами поглощения! они являются следствиями остальных свойств, что показано нижед Свойства 11-12 - законы де Моргана. Свойство 13
; свойства 5-6 - взаимную дистрибутивность этих операций, что дает возможность раскрывать скобки в формулах. Свойства 7-8 -устранение кратности; свойства 9-10 называют правилами поглощения! они являются следствиями остальных свойств, что показано нижед Свойства 11-12 - законы де Моргана. Свойство 13
называют законом исключенного третьего; свойство 14 - законом противоречия. Свойства 15-20 характеризуют основные операции над переменной и константами 0 и 1. Свойство 21 - снятие двойного отрицания.|
Совокупность всех булевых функций  с тремя данными
с тремя данными
операциями есть алгебра 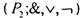 . Она называется алгеброй
. Она называется алгеброй
булевых функций, алгеброй логики, а также булевой алгеброй. Сравнивая свойства 1-21 для булевых функций со свойствами 1-21 §1 главы 1 для алгебры множеств, приходим к следующему результату.
Соотношение между булевой алгеброй и алгеброй Кантора есть изоморфизм, порождаемый соответствием между подмножествами
конечного п -элементного множества М и п -мерными булевыми векторами вместе с соответствием между операциями объединения, пересечения, дополнения для множеств и операциями дизъюнкции, конъюнкции и отрицания для векторов. При этом соответствии сохраняются все свойства операций, их определяющие.
Вследствие описанного изоморфизма всякую алгебру, которая обладает свойствами 1-21, называют булевой алгеброй. Кроме алгебры Кантора и алгебры логических функций, булевой алгеброй является, например, алгебра случайных событий в теории вероятностей.
Упражнение. Разберите самостоятельно, что соответствует в алгебре Кантора и в алгебре случайных событий булевым функциям
 , константам 0 и 1. Некоторые рассмотренные выше функции выражаются через
, константам 0 и 1. Некоторые рассмотренные выше функции выражаются через
 и эти выражения тоже представляют эквивалентности:
и эти выражения тоже представляют эквивалентности:

Для функций  справедливы также
справедливы также
соотношения:


Важнейшее свойство равенства булевых функций состоит в том,
что если в суперпозиции  заменить какую-либо
заменить какую-либо
функцию  на равную ей, то это не повлияет на результат Указанная
на равную ей, то это не повлияет на результат Указанная
процедура представляет правило замены подформул.
С другой стороны, если в формуле  , выражающей равенство
, выражающей равенство
(эквивалентность формул) двух булевых функций заменить какую-либо переменную X на произвольную формулу  , то полученные формулы
, то полученные формулы
 представляют уже две другие функции
представляют уже две другие функции  , но
, но
равенство между ними сохраняется:  . Подчеркнем, что должны
. Подчеркнем, что должны
одновременно заменяться все вхождения переменной X, Так, из равенства (13) получается равенство 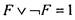 , верное для любой
, верное для любой
формулы F. Однако частичная замена  уже не дает верного
уже не дает верного
равенства.
Правильная подстановка и замена подформул приводит к новым эквивалентным соотношениям.
Несколько следствий основных равенств:
1) поглощение: а) свойство 9: 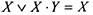 ; (*) Доказательство:
; (*) Доказательство: 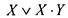 = [в силу свойства 18]=
= [в силу свойства 18]=  =
=
[выносим X за скобки] =  = [в силу свойств 17,18] =
= [в силу свойств 17,18] = 
б) свойство 10:  ;
;
Доказательство: 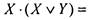 [раскрываем скобки]
[раскрываем скобки]

2) склеивание:  ;
;
Доказательство  ; [выносим X за скобки]
; [выносим X за скобки]

Доказательство'  [заменяем X на левую часть
[заменяем X на левую часть
равенства (*)] =  = [выносим Y за скобки из двух
= [выносим Y за скобки из двух
последних слагаемых] =  = [в силу свойства 13]
= [в силу свойства 13]
Обратите  внимание, что равенства 7-10, 13-18 и указанные следствия содержат в правой части меньше символов (более короткие
внимание, что равенства 7-10, 13-18 и указанные следствия содержат в правой части меньше символов (более короткие
формулы), чем в левой Поэтому применение этих эквивалентностей позволяет осуществлять преобразования, в частности, упрощения формул, выражать одни из функций через другие; некоторые примеры такого рода уже встречались.
Возникают естественные вопросы
(1) можно ли суперпозициями функций одной-двух переменных выразить любую функцию большего числа переменных;
(2) как это сделать, если это возможно. Ответ на эти вопросы - в следующем разделе.
Дата публикования: 2014-11-18; Прочитано: 9162 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
