 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Булева функция (логическая функция, функция алгебры
|
|
^логики) - это функция одной или нескольких переменных
I  , где
, где  Z - логические переменные,
Z - логические переменные,
' т.е. и значения аргументов, и значение функции - ноль или единица. Тем самым, булева функция п переменных есть функция на 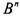 •г множестве п -мерных векторов
•г множестве п -мерных векторов 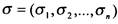 , компоненты которых
, компоненты которых
'равны 0 или 1:  . Можно применять векторные обозначения
. Можно применять векторные обозначения
|для сокращения записи. Пользуясь другими терминами, можно
f 
[считать областью определения булевой функции множество вершин
i п -мерного единичного куба 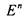
.На рис.19 изображена
Гфункция 3 переменных
f 
fпринимающая значение 1 на
t1наборах (001), (011), (100)
[Обратите внимание на допустимую
форму записи: можно не разделять запятыми значения аргументов -все они однозначные числа.
;Если число переменных равно
п и любая из них может независимо от других принимать 2:значения, то число различных п -
 векторов равно
векторов равно 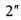 . Относительно
. Относительно
t
каждой функции  все множество
все множество  разбивается
разбивается
на два класса // -векторов прообраз значения 0 и прообраз значения
1 функции Z Мы будем рассматривать только всюду определенные функции
Если считать, что переменные  обозначают истинность
обозначают истинность
(значение 1) или ложность (значение 0) высказываний-аргументов, то
функция Z выражает истинность или ложность определенного сложного высказывания при различных сочетаниях значений аргументов Например, конъюнкция двух высказываний - это сложное высказывание, истинное тогда и только тогда, когда истинны оба составляющих простых высказывайся. С функциональной точки зрения конъюнкцию можно рассматривать как булеву функцию двух логических переменных, принимающую значение 1 тогда и только тогда, когда оба аргумента равны 1.
Для задания логической функции нужно указать каким-либо образом, какое значение принимает функция на тех или иных наборах значений аргументов. Поэтому естественным является табличное представление булевых функций -для функции
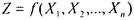 - таблица из
- таблица из  строк - п -мерных булевых векторов в алфавитном порядке, каждому из которых сопоставлено значение функции Z, равное 0 или 1. Заметим, что булева функция Z является на
строк - п -мерных булевых векторов в алфавитном порядке, каждому из которых сопоставлено значение функции Z, равное 0 или 1. Заметим, что булева функция Z является на  характеристической функцией того множества точек
характеристической функцией того множества точек
 , для которых Z = 1. В таблице 5 представлены все функции одной переменной - их 4
, для которых Z = 1. В таблице 5 представлены все функции одной переменной - их 4
В 1 -м столбце - значения переменной X; в каждом из последующих -значения соответствующей функции, обозначение функции - в 1-й
строке Во 2-м столбце - функция-константа  , в 5-м - функция-
, в 5-м - функция-
константа 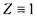 . В 3-м столбце тождественная функция Z = X, в 4-м -
. В 3-м столбце тождественная функция Z = X, в 4-м -
функция  , которую обозначают также
, которую обозначают также  и называют
и называют
отрицанием. Второй способ обозначения подчеркивает, что отрицание
- одноместная функция аргумента X.
Аналогично могут быть заданы функции нескольких переменных Некоторые из них - для двух переменных - в табл.6 Сравните их (столбцы 3-5) с таблицами истинности основных логических операций конъюнкции, дизъюнкции, импликации, эквивалентности,'для которых значения аргументов и результатов операций обозначались буквами И, Л Отметим также, что с арифметической точки зрения, т.е. если рассматривать 0 и 1 как натуральные числа с обычными операциями
арифметики,  выполнены равенства:
выполнены равенства:
Поэтому конъюнкцию  называют умножением и записывают
называют умножением и записывают
со знаком произведения:  или вообще - как в алгебре - без
или вообще - как в алгебре - без
знака: XY. Дизъюнкцию иногда удобно называть логическим сложением, а связываемые ею члены - логическими, или дизъюнктивными слагаемыми. Однако следует иметь в виду, что, во-первых, на наборе (1, 1) значение дизъюнкции не совпадает с арифметической суммой, а, во-вторых, термин "сумма" для логических переменных употребляется и в другом значении, представленном в той же табл.6. В двух последних столбцах табл.6 представлены функции, которые не встречались раньше, а именно:
Сумма по модулю 2 - функция двух переменных, равная 0, если значения аргументов совпадают, и 1 в противном случае; ее обозначение
-  . Арифметическое значение
. Арифметическое значение  -остаток от деления числа
-остаток от деления числа
(X + Y) на 2, - отсюда название. Другое название - неэквивалентность,
поскольку выполнено тождество: 
Сумма по модулю 2 как бинарная операция обладает свойствами
коммутативности и ассоциативности  , и поэтому
, и поэтому
ее можно записывать без скобок  и переставлять слагаемые.
и переставлять слагаемые.
Штрих Шеффера - функция двух переменных, равная 0 тогда и
только тогда, когда оба аргумента равны 1. Обозначение:  , условное
, условное
название " X несовместно с Y". Выполнены тождества:

Если принять, что всевозможные наборы значений двух аргументов (как легко видеть, их 4) расположены в таблице в алфавитном порядке, то каждая функция двух переменных полностью задается столбцом
значений длины 4. Так же, булевым вектором длины 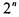 задается логическая функция п переменных. Для удобства записи можно транспонировать столбец значений в строку и таким сокращенным
задается логическая функция п переменных. Для удобства записи можно транспонировать столбец значений в строку и таким сокращенным
способом задавать булевы функции. Например,  представляет
представляет
конъюнкцию,  - дизъюнкцию,
- дизъюнкцию,  - импликацию;
- импликацию;
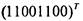 представляет функцию трех переменных
представляет функцию трех переменных  , заданную в
, заданную в
последнем столбце табл.7. Для получения таблицы нужно приписать слева к столбцу значений стандартный (для каждого п) перечень всех /; -наборов, расположенных в алфавитном порядке, т.е. описанную
в §4 гл 2 таблицу 
Для задания булевой функции наряду с транспонированным столбцом значений функции можно использовать сокращенную запись: кортеж номеров тех строк таблицы, где функция равна 1 (номера могут быть записаны в десятичной системе в возрастающем порядке).
Например, функцию 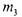 из табл.7 можно задать кортежем: [3,5,6,7], а
из табл.7 можно задать кортежем: [3,5,6,7], а
функцию  из той же таблицы - [0, 1, 4, 5]. Это особенно удобно, если
из той же таблицы - [0, 1, 4, 5]. Это особенно удобно, если
функция принимает значение Ьна небольшом числе наборов, по сравнению с их общим количеством.
Упражнение. Обязательно ли при таком задании функции указывать число переменных?
Важный пример применения булевых функций дают арифметические действия над двоичными числами: поскольку возможные знаки в двоичной системе суть 0 и 1, то зависимости знаков результата от знаков слагаемых/сомножителей выражаются булевыми
функциями. При сложении двух однозначных двоичных чисел А и В знак суммы в младшем разряде равен  , а знак переноса
, а знак переноса 
возникает только если оба слагаемых равны 1, т.е.  Умножение однозначных двоичных чисел тождественно конъюнкции, что фактически отмечено выше.
Умножение однозначных двоичных чисел тождественно конъюнкции, что фактически отмечено выше.

В табл.7 представлены 3 функции трех переменных. Первую из них
 называют иногда функцией большинства - ее значение
называют иногда функцией большинства - ее значение
равно значению, которое принимает большинство аргументов (т.е. два или три): если в наборе больше единиц, чем нулей, то и значение функции равно 1. Заметим, что при сложении двух многозначных двоичных чисел в каждом разряде, кроме самого младшего, складываются 3 однозначных числа: знаки двух слагаемых в этом разряде и знак переноса из предыдущего разряда. Таким образом, знак суммы как логическая функция есть сумма по модулю 2 трех булевых переменных. Знак переноса 1 возникает, если при таком сложении знаков число
единиц равно 2 или 3, т.е. он равняется значению функции большинства от тех же d переменных.
В той же таблице заданы две другие функции, обозначенные 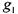 и
и  . По форме - это функции трех переменных, однако нетрудно убедиться, что
. По форме - это функции трех переменных, однако нетрудно убедиться, что  . как видим, функция
. как видим, функция 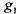 не зависит
не зависит
от аргумента Y, а функция  от аргументов X, Z. Действительно, если, например, X = 0,7 = 1, то и при Y = О (набор 001), и при Y = \ (набор 011) выполнено равенство
от аргументов X, Z. Действительно, если, например, X = 0,7 = 1, то и при Y = О (набор 001), и при Y = \ (набор 011) выполнено равенство  . Таким же образом проверяются
. Таким же образом проверяются
остальные 3 сочетания переменных X и Z. Введем определение Несущественные (фиктивные) переменные: для функции
 переменная
переменная  называется
называется
несущественной, если выполнено 
 при всех значениях
при всех значениях

Таким образом, для функции  несущественной переменной является Y, а для функции
несущественной переменной является Y, а для функции  - несущественные переменные X и Z. Если относить к функциям п переменных и функции, существенно
- несущественные переменные X и Z. Если относить к функциям п переменных и функции, существенно
зависящие не от всех своих переменных (т.е. являющиеся по существу функциями меньшего числа переменных), то общее число функций п переменных равно числу
булевых векторов длины  , т.е.
, т.е.  . Для одной переменной это число равно 4 (см.
. Для одной переменной это число равно 4 (см.
табл.5); для двух переменных - 24 =16; сщя трех переменных - 28 = 256; для
нетырех переменных -2|6 = 65536и т.д.  Таблица всех 16 функций 2 переменных содержится в файле материалов. Множество всех логических функций, от любого конечного числа
Таблица всех 16 функций 2 переменных содержится в файле материалов. Множество всех логических функций, от любого конечного числа
переменных обозначается 
Если  - фиктивная переменная функции
- фиктивная переменная функции 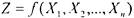
то первая половина задающего ее столбца значений совпадает со второй, и если отбросить вторую половину таблицы этой функции и затем удалить 1-й столбец (состоящий из нулей), то останется таблица
некоторой функции (п -1) переменных  . Аналогично, если
. Аналогично, если 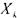
- фиктивная переменная функции  и вычеркнуть
и вычеркнуть
из таблицы столбец переменной  и все строки с единичным
и все строки с единичным
значением  (т е строки, в которых
(т е строки, в которых  ), то останется таблица
), то останется таблица
функции  . Будем говорить, что g
. Будем говорить, что g
получается из  удалением, а
удалением, а  - введением фиктивной
- введением фиктивной
переменной 
Функции, которые могут быть получены друг из друга удалением и введением фиктивных переменных, считаются равными. Очевидно,
равенство функций есть отношение эквивалентности на  , поэтому множество всех булевых функций разбивается на классы равных
, поэтому множество всех булевых функций разбивается на классы равных
функций. В этом смысле, использованные выше записи 
 - правильны, т.е. функция
- правильны, т.е. функция  равна функции двух переменных
равна функции двух переменных 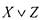 , имеющей столбец значений
, имеющей столбец значений  , а функция
, а функция 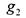 равна
равна
функции одной переменной Y, имеющей столбец значений 
Понятно, что удаление фиктивных переменных делает задание функции таблицей более компактным. Однако и введение фиктивных переменных может быть полезным: некоторую совокупность функций от разных множеств переменных можно рассматривать как зависящую от одного и того же множества переменных - объединения множеств переменных всех функций совокупности, если это объединение конечно.
Дата публикования: 2014-11-18; Прочитано: 2659 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
