 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Матричные игры. Смешанные стратегии. Основная теорема теории игр
|
|
Пусть у первого игрока имеются ходы  , а у второго игрока –
, а у второго игрока –  .
.
Такая игра называется игрой с нулевой суммой, так как  .
.
Игра называется онтогонистической, так как величину, которую выигрывает первый игрок, второй игрок проигрывает.
Игра называется матричной, так как она характеризуется матрицей выигрышей 

Отдельный розыгрыш или исход игры осуществляется следующим образом: первый игрок тайным образом выбирает свой ход  , т.е. он выбирает
, т.е. он выбирает 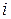 -ю строку матрицы
-ю строку матрицы 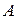 , а второй игрок выбирает ход
, а второй игрок выбирает ход  , т.е.
, т.е. 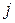 -ый столбец матрицы
-ый столбец матрицы 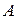 . На пересечении
. На пересечении 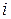 -ой строки и
-ой строки и 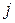 -го столбца находится элемент
-го столбца находится элемент  . Тогда первый игрок выигрывает это число, а второй проигрывает (должен заплатить ему это число). Розыгрыши могут повторяться некоторое количество раз. Ясно, что первый игрок должен выбирать такой свой ход
. Тогда первый игрок выигрывает это число, а второй проигрывает (должен заплатить ему это число). Розыгрыши могут повторяться некоторое количество раз. Ясно, что первый игрок должен выбирать такой свой ход  , чтобы
, чтобы 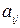 было как можно больше 0, а второй –
было как можно больше 0, а второй –  таким образом, чтобы
таким образом, чтобы 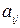 было меньше 0.
было меньше 0.
Определение. Вектор  ,
,  ,
,  называется смешанной стратегией первого игрока, где
называется смешанной стратегией первого игрока, где  означает вероятность (при бесконечном количестве розыгрышей), либо частоту, с которой он выбирал свои ходы
означает вероятность (при бесконечном количестве розыгрышей), либо частоту, с которой он выбирал свои ходы  .
.
Определение. Вектор  ,
,  ,
,  называется смешанной стратегией второго игрока, где
называется смешанной стратегией второго игрока, где 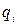 означает вероятность либо частоту, с которой второй игрок выбирает свой ход
означает вероятность либо частоту, с которой второй игрок выбирает свой ход  .
.
Определение. Пусть  – множество смешанных стратегий первого игрока,
– множество смешанных стратегий первого игрока, 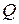 – множество смешанных стратегий второго игрока. Если зафиксировать
– множество смешанных стратегий второго игрока. Если зафиксировать  и в ней окажется больше нулей, то ход
и в ней окажется больше нулей, то ход  будем называть активным, а если
будем называть активным, а если  , то ход называется пассивным.
, то ход называется пассивным.
Определение. Если зафиксировать  и в ней
и в ней  , то ход активен, а если
, то ход активен, а если  , то
, то  пассивен.
пассивен.
Теорема (основная теорема теории игр). В любой матричной игре существует  – оптимальная смешанная стратегия первого игрока и
– оптимальная смешанная стратегия первого игрока и  – оптимальная смешанная стратегия второго игрока такие, что
– оптимальная смешанная стратегия второго игрока такие, что  ,
,  ,
, 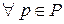 . При этом
. При этом  называется ценой игры.
называется ценой игры.
10. Сведение матричных игр к паре взаимодвойственных задач ЛП.
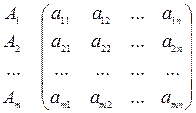
Пусть первый игрок придерживается смешанной стратегии  .
.
Если второй игрок выбирает свой чистый ход  , то выигрыш первого игрока будет
, то выигрыш первого игрока будет

 , тогда
, тогда  .
.
Делим все неравенства системы на положительное число  и введем обозначение
и введем обозначение  ,
,  .
.
 (7)
(7)
для любого 
 (8)
(8)

Так как первый игрок стремиться выиграть как можно больше, т.е.  , тогда для второго игрока
, тогда для второго игрока 
 (9)
(9)
Таким образом, для первого игрока получаем задачу линейного программирования (9) – (7), для нее всегда строится начальный двойственный базовый план, применяя двойственный симплекс-метод, мы через конечное число итераций найдем 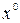 – оптимальный план.
– оптимальный план.
Замечание. Можно доказать, что у задачи (9) – (8) – (7) всегда существует оптимальный план, тогда из наших замен вытекает, что  – цена игры
– цена игры  ,
,  – оптимальная смешанная стратегия первого игрока.
– оптимальная смешанная стратегия первого игрока.
Таким образом, решение игры для первого игрока свелось к решению задачи линейного программирования (9) – (8) – (7).
Второй игрок.
Пусть второй игрок выбирает некоторую смешанную стратегию  .
.
Если первый игрок выбирает ход  , то проигрыш второго будет
, то проигрыш второго будет


Делим эту систему на  и вводим обозначение
и вводим обозначение 
 (10)
(10)
 (11)
(11)
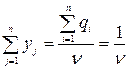 ,
,  , тогда
, тогда 
 (12)
(12)
Приходим к задаче линейного программирования (12) – (11) – (10). Она имеет нормальную форму, у нее строим начальный базовый план и применяем принцип прямого симплекс-метода.
Можно доказать, что у задачи всегда существует 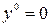 , тогда
, тогда  – цена игры,
– цена игры, 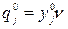 – …?….. оптимальный план смешанной стратегии второго игрока.
– …?….. оптимальный план смешанной стратегии второго игрока.
Таким образом, в решении игры второго игрока мы приходим к задаче линейного программирования (12) – (11) – (10). Не трудно заметить, что пара задач (9) – (8) – (7) и (12) – (11) – (10) взаимнодвойственны
 (13)
(13)
 (14)
(14)
11. Метод Брауна-Робинсона в решение матричных игр.
Пусть имеется матричная игра

В некоторых случаях, если 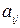 подсчитаны приближенно, нет смысла находить и точное значение для
подсчитаны приближенно, нет смысла находить и точное значение для  и
и  . Поэтому разработаны специальные методы приближенного решения матричных игр, в которых широко используется вычислительная техника. Производится, как правило, искусственное разыгрывание игры. Разыгрывание определяется по конечное число партий. По результатам розыгрыша подсчитывается приближенный выигрыш (проигрыш) игроков и частоты
. Поэтому разработаны специальные методы приближенного решения матричных игр, в которых широко используется вычислительная техника. Производится, как правило, искусственное разыгрывание игры. Разыгрывание определяется по конечное число партий. По результатам розыгрыша подсчитывается приближенный выигрыш (проигрыш) игроков и частоты  ,
,  выбор первым игроком своих ходов
выбор первым игроком своих ходов 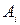 и
и
 ,
, 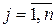 частоты выбора второго игрока своих ходов
частоты выбора второго игрока своих ходов  .
.
 ,
,  .
.
Дата публикования: 2014-11-18; Прочитано: 845 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
