24. Естественный отбор 159
| Таблица 24.13. Изменение частот аллелей за одно поколение отбора против гетерозигот
|
|
|
| Генотип
|
|
|
|
|
|
|
|
| Всего
| Частота a
|
|
|
| АA
| Аа
| аа
|
|
|
| 1.
| Исходная частота зигот
| 
| 
| 
| 
| 
|
| 2.
| Приспособленность (w)
| 
| 
| 
| 
| 
|
| 3.
| Вклад каждого генотипа в следующее поколение
| 
| 
| 
| 
| 
|
| 4.
| Нормализованная частота
| 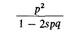
| 
| 
| 
| 
|
| 5.
| Изменение частоты аллеля
| 
| 
| 
| 
| 
|
Изменение частот аллелей равно нулю, когда ∆ q = 0. Это условие выполняется при ρ = q. (Последнее справедливо лишь при одинаковой приспособленности обеих гомозигот. Если же их приспособленности различны, то различны и равновесные частоты аллелей.) Однако равновесие при этом неустойчиво. В том случае, когда q > ρ, значение ∆q положительно и q возрастает до тех пор, пока аллель А не будет элиминирован из популяции. Если же q < ρ, то значение ∆q отрицательно и частота аллеля а будет продолжать уменьшаться, стремясь к нулю. Таким образом, если популяция вначале не находится точно в состоянии равновесия, она будет все больше удаляться от него до тех пор, пока аллель, частота которого исходно была ниже равновесной, не будет вытеснен из популяции. Если же популяция вначале находится в состоянии неустойчивого равновесия, то случайные отклонения от равновесия в результате дрейфа генов или каких-то других причин приведут к тому, что тот или иной аллель окажется вытесненным из популяции (рис. 24.7).

|
| Рис. 24.7. Изменение частот аллелей при отборе против гетерозигот в случае, когда обе гомозиготы обладают равными приспособленностями. Равновесие (∆ q = 0), достигаемое при q = 0,5, неустойчиво: если популяция изначально не находится
| в состоянии равновесия, то она в дальнейшем удаляется от него и аллель, частота которого в начальный момент была меньше равновесной, элиминируется из популяции.
|