Определение диапазона трансмиссии

Кинематический расчет трансмиссии сводится к определению передаточных чисел агрегатов и механизмов, составляющих трансмиссию машины.

Для определения передаточных чисел КП и БП необходимо знать реализуемый на дорогах диапазон скоростей движения гусеничной машины.

При расчетах ступенчатых механических трансмиссий пользуются кинематическим диапазоном, который определяется как отношение максимальной скорости к минимальной при одной и той же частоте вращения коленчатого вала двигателя:

d_k = или , (2.10)

где: ί_o – общее передаточное число трансмиссии.

Современные гусеничные машины с механической (зубчатой) трансмиссией имеют кинематический диапазон порядка d_к = 6…10.

Чем выше диапазон, тем шире скоростные и тяговые качества машины.

Однако при большом диапазоне увеличивается необходимое число передач, усложняется конструкция коробки передач и затрудняется управление.

Определение минимальной скорости движения машины производят из условия равномерного движения ее на максимальном подъеме с использованием полученной максимальной мощности двигателя:

V_min = , (2.11)

где: η_о - общий КПД машины, определяемый по формуле (2.5), причем в этой формуле значение V можно ориентировочно принять равным V= 5…7 км/ч.

ψ = ƒ·cosα_max + sinα_max (2.12)

При расчетах принимают достаточно трудный для движения на максимальный подъем грунт с коэффициентом сопротивления качению

ƒ = 0,08…0,1, обладающий высоким коэффициентом сцепления

φ = 0,8…1,0.

При определении минимальной скорости рассчитанная максимальная сила тяги по двигателю не должна превышать силу тяги по сцеплению, т.е.

G · (ƒ · cosα_max + sinα_max) ≤ G · cosα_max · φ (2.13)

При значительном отклонении максимальной силы тяги по двигателю от силы тяги по сцеплению происходит недоиспользование мощности двигателя, поэтому в этом случае требуется перерасчет минимальной скорости движения по формуле:

V_min = .

Разбивка диапазона трансмиссии по передачам и

определение передаточных чисел

Наибольшая скорость движения достигается у машины с бесконечно большим числом передач и работе двигателя на режиме максимальной мощности.

С другой стороны, дешевле и предпочтительнее по условиям изготовления и эксплуатации ступенчатая коробка с минимальным числом передач.

Для получения минимального числа передач в коробке необходимо использовать весь рабочий диапазон изменения частоты вращения коленчатого вала двигателя от n_т до n_p.

Рис. 2.1. Рабочий диапазон изменения частоты вращения

коленвала двигателя

Это позволяет использовать для разгона на всех передачах одну и ту же среднюю мощность двигателя. Таким образом, для плавного переключения передач с одной на другую необходимо, чтобы скорость, с которой начинается разгон на данной передаче (II), была равна скорости в конце разгона на предыдущей передаче (I).

Равенство указанных скоростей выражается уравнением:

(2.14)

где: r_k - радиус ведущего колеса;

i_km, i_k(m-1) – передаточные числа коробки, соответственно на передаче

номер m и передаче m-1;

i_n – постоянное передаточное число трансмиссии, которое обеспечивается бортовой передачей.

Из приведенного уравнения (2.14) следует, что передаточные числа коробки передач должны удовлетворять условию:

. (2.15)

Учитывая, что на всех передачах диапазон частот вращения должен быть одинаковым, указанное соотношение (2.15) будет иметь вид:

, (2.16)

что предполагает построение ряда передаточных чисел коробки передач по принципу геометрической прогрессии.

Полагая V₁ = V_min, V_m = V_max, получим:

V₂ = V₁·q

V₃ = V₁·q² (2.17)

........

V_m = V₁·q^m-1

где: q – знаменатель геометрической прогрессии, определяемый из выражения:

q = (2.18)

Очевидно, чем больше число передач m, тем меньше q и ближе к n_p частота вращения, с которой начинается разгон машины.

При проектировании машины возникает необходимость определения минимального числа передач, которое необходимо иметь в КП при данном ее кинематическом диапазоне. Для получения формулы числа передач прологарифмируем выражение (2.18) и заменим в нем q = , тогда

m = 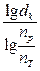+ 1. (2.19)

Дробный результат округляется до ближайшего целого числа. После этого уточняется значение q по формуле (2.18) и определяются передаточные числа промежуточных передач коробки:

i_к(m-1)= i_km·q. (2.20)

У большинства гусеничных машин первая передача не является транспортной, т.е. в движении не производится переключение с первой на вторую передачу. «Отрыв» первой передачи от остальных объясняется использованием ее как замедленной с целью получения максимальной силы тяги при преодолении максимальных сопротивлений дороги и использования машины как эвакосредства. Указанный «отрыв» первой передачи обычно проводят, если расчетная минимальная скорость машины получилась в пределах около 2 м/с. В этом случае величина d_к, подставляемая в формулу (2.19), определится:

d_к = (2.21)

где: V₂ – cкорость на второй передаче, принимая:

V₂ = (2,0…2,5) · V_min.

Передаточное число высшей передачи у гусеничных машин по соображениям согласования скоростной и тяговой характеристик машины обычно составляет 0,7…0,8.

После разбивки диапазона скоростей по передачам и установления числа передач определяется постоянное передаточное число трансмиссии по формуле:

. (2.22)

В этой формуле величину i_km можно, как уже отмечалось, принимать в пределах 0,7…0,8.

Для гусеничных тягачей величина i_n обычно находится в пределах 6…7, для танков 7…12.

Причем, при i_n > 7 необходимо устанавливать двойную или планетарную бортовую передачу.

Для I-ой и II-ой передач передаточные числа коробки определяются исходя из расчетной скорости с использованием формулы (2.22):

i_кm = .

Если первая передача коробки входит в транспортный ряд скоростей движения машины, то все остальные промежуточные передаточные числа можно определить по формуле (2.20).

Если же первая передача выполнена с «отрывом», то по расчетной скорости на 2-й передаче определяют ее передаточное число, после чего используется та же формула (2.20).