Метод Симпсона (парабол)

При n =2 (i = 0,1,2) из формулы (1) последовательно находим:

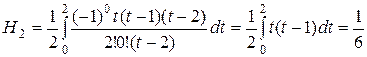
Тогда на отрезке [ x₀, x₂ ] получим:

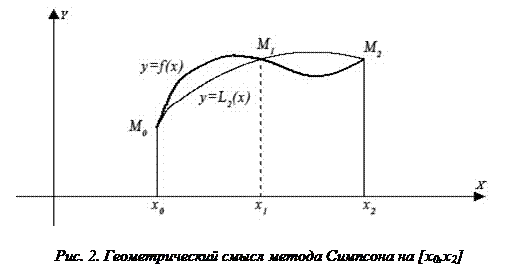
Геометрический смысл метода Симпсона (парабол) заключается в том, что исходную функцию f(x) заменяют интерполяционным многочленом 2-й степени, т.е. параболой, проходящей через точки M₀(x₀,y₀), M₁(x₁,y₁), M₂(x₂,y₂) (рис. 2).

Если считать, что n – четное (n = 2m), то на отрезке [ a,b ]=[ x_0, x₂ ] U [ x₂, x₄ ] U... U[ x_n-2, x_n ] имеем:

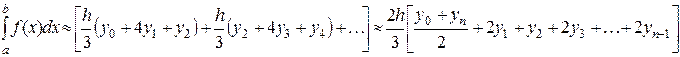
Для составления программы формулу Симпсона следует преобразовать (прибавить и отнять y_n):

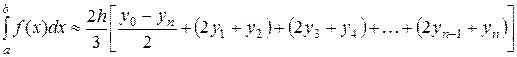(4)

Остаточный член формулы Симпсона оценивается следующей формулой:

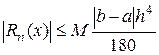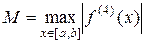, где (5)

Методы прямоугольников

Простейшими методами численного интегрирования являются методы левых и правых прямоугольников. Данные методы используют замену определенного интеграла интегральной суммой:

, где .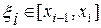

Разобьем отрезок [ a,b ] на n равных частей: . С учетом этого условия получим: .

Рассмотрим три случая.

1) Точки – левые концы отрезков 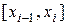, где :

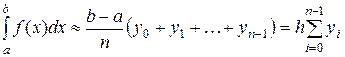– формула левых прямоугольников (рис. 3).

2) – правые концы отрезков :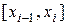

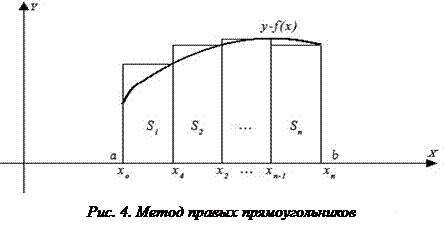
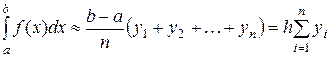– формула правых прямоугольников (рис. 4).

3) – середины отрезков :

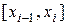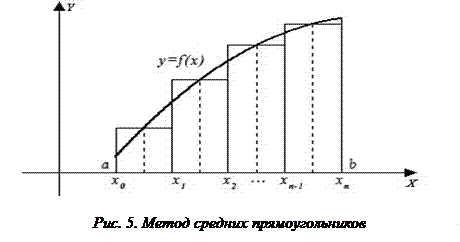
– формула средних прямоугольников (рис. 5).

Из трех рассмотренных методов прямоугольников метод средних прямоугольников является более точным. Среди таких методов численного интегрирования, как метод трапеций, метод Симпсона и методы прямоугольников наиболее точный метод – это метод Симпсона (парабол).

Остаточный член формулы левых и правых прямоугольников оценивается соответственно по формулам:

(6), (7), где .

Остаточный член формулы средних прямоугольников:

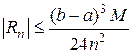, где (8)