Рассмотрим возможность использования рассмотренных выше методов при определении положений звеньев для механизмов, структурная формула которых I – II1 – II2. Для примера допустим, что решается задача кинематического исследования механизма, показанного на рис. 2.35. В таких механизмах при определенных размерах звеньев и относительном расположении неподвижных кинематических пар можно получить двойной ход ползуна Е за один оборот кривошипа ОА. Эта особенность используется, например, в грохотах, плунжерных насосах.
Встроенный механизм шарнирного четырехзвенника был рассмотрен в качестве примера в разделе 2.5.2 (см. рис. 2.32). Там же в табл. 2.1 приведены координаты точек звеньев и угловые положения самих звеньев в декартовой системе координат XOY. В табл. 2.1 приведены, координаты точек связи C (XC, YC)в системе координат XOY. Чтобы воспользоваться методом решения задачи из раздела 2.5.3, введем новую систему координат X 1 DY 1. Для этого линейным преобразованием переведем координаты связи C (XC, YC)в координаты (X 1 С, Y 1 С)системы координат X 1 DY 1. Имеем
 (2.50)
(2.50)
где XD, YD – координаты точки D в системе координат XOY,
ψ – угол поворота осей системы координат X 1 DY 1.
Далее на основании формул (2.46)...(2.49) находим угловое положение шатуна СЕ,координаты ползуна Х 1 Е, Y 1 E и координаты точки S шатуна X 1 S, Y 1 S.
В расчетах принято: ось абсцисс X 1проходит через кинематическую пару D угол поворота осей координат ψ = 180°. Длина шатуна  = 0,6м, положение точки S 4заданно расстоянием
= 0,6м, положение точки S 4заданно расстоянием  = 0,4м.
= 0,4м.

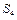 X X
| |
 X X
| |
 X X
| |





Рис.2.35. Механизм с двойным ходом ползуна
В табл. 2.2 приведены значения кинематических параметров для положений ведущего звена, соответствующих координатнй системе X 1 DY 1.
Таблица 2.2

 (2.50)
(2.50) = 0,6м, положение точки S 4заданно расстоянием
= 0,6м, положение точки S 4заданно расстоянием  = 0,4м.
= 0,4м.




 Рис.2.35. Механизм с двойным ходом ползуна
Рис.2.35. Механизм с двойным ходом ползуна

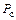

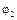

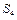 X
X

 X
X

 X
X
