Пример 2. Когда выражение под знаком предела находится в степени – это первый признак того, что нужно попытаться применить второй замечательный предел

Найти предел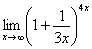

Когда выражение под знаком предела находится в степени – это первый признак того, что нужно попытаться применить второй замечательный предел.

Но сначала, как всегда, пробуем подставить бесконечно большое число в выражение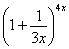

Нетрудно заметить, что при 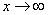основание степени 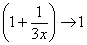, а показатель – 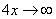, то есть имеется, неопределенность вида :

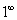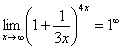
Данная неопределенность как раз и раскрывается с помощью второго замечательного предела. Но, как часто бывает, второй замечательный предел не лежит на блюдечке с голубой каемочкой, и его нужно искусственно организовать. Рассуждать можно следующим образом: в данном примере параметр 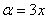, значит, в показателе нам тоже нужно организовать 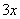. Для этого возводим основание в степень 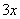, и, чтобы выражение не изменилось – возводим в степень :

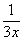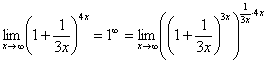
Когда задание оформляется от руки, карандашом помечаем:

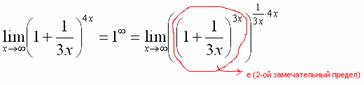
Практически всё готово, страшная степень превратилась в симпатичную букву :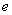

При этом сам значок предела перемещаем в показатель.

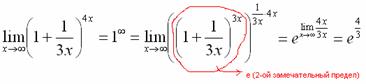
ПРАКТИКУМ 21

ЗАДАНИЕ N 1
Тема: Первый замечательный предел
…

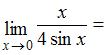Решение:
Чтобы воспользоваться первым замечательным пределом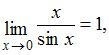
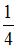необходимо, используя соотношение вынести множитель за знак предела. Тогда: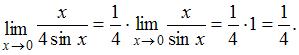

ЗАДАНИЕ N 2
Тема: Первый замечательный предел
…

Решение:
Чтобы воспользоваться первым замечательным пределом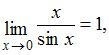
необходимо, используя соотношение вынести множитель 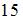за знак предела. Тогда: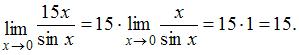

ЗАДАНИЕ N 3
Тема: Второй замечательный предел
Пусть 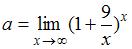. Тогда 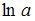равен …

Решение:
Обращаем внимание, что функцию 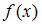нужно преобразовать так, чтобы использовать второй замечательный предел – формулу .
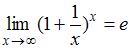Для этого числитель и знаменатель дроби необходимо разделить на число ,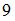
получается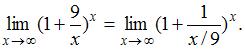
Далее нужно выполнить замену переменной, полагая 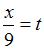. Тогда если ,
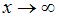то 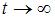, 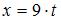и, следовательно,
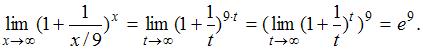Получаем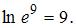

ЗАДАНИЕ N 4
Тема: Второй замечательный предел
Пусть 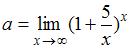. Тогда 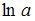равен …

Решение:
Обращаем внимание, что функцию 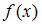нужно преобразовать так, чтобы использовать второй замечательный предел – формулу .
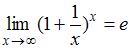Для этого числитель и знаменатель дроби необходимо разделить на число ,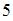
получается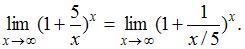
Далее нужно выполнить замену переменной, полагая 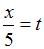. Тогда если ,
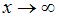то 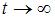, 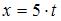и, следовательно,
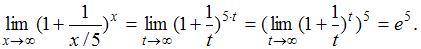Получаем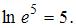

САМОСТОЯТЕЛЬНАЯ РАБОТА 21

ЗАДАНИЕ N 1
Тема: Первый замечательный предел
…

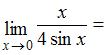ЗАДАНИЕ N 2
Тема: Первый замечательный предел
…

ЗАДАНИЕ N 3
Тема: Первый замечательный предел
…

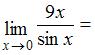ЗАДАНИЕ N 4
Тема: Второй замечательный предел
Пусть 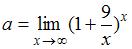. Тогда 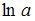равен …

ЗАДАНИЕ N 5
Тема: Второй замечательный предел
Пусть 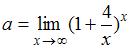. Тогда 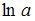равен …

ЗАДАНИЕ N 6
Тема: Второй замечательный предел
Пусть 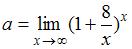. Тогда 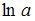равен …