Пример 6. Найти предел Максимальная степень «икса» в числителе: 2 Максимальная степень «икса» в знаменателе: 1 ( можно записать как )

Найти предел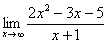
Максимальная степень «икса» в числителе: 2
Максимальная степень «икса» в знаменателе: 1 (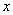 можно записать как )
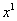Для раскрытия неопределенности 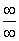необходимо разделить числитель и знаменатель на 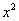. Чистовой вариант решения может выглядеть так:

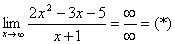
Разделим числитель и знаменатель на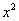

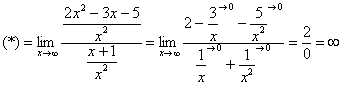
Под записью 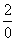подразумевается не деление на ноль (делить на ноль нельзя), а деление на бесконечно малое число.

Таким образом, при раскрытии неопределенности вида 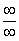у нас может получиться конечное число, ноль или бесконечность.

ПРАКТИКУМ 20

ЗАДАНИЕ N 1
Тема: Раскрытие неопределенности вида "ноль на ноль"

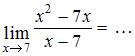
Решение:
Если вместо переменной 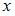поставить значение 7, к которому она стремится, то получим неопределенность ви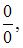да тогда

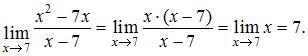
ЗАДАНИЕ N 2
Тема: Раскрытие неопределенности вида "ноль на ноль"

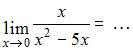
Решение:
Если вместо переменной 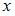поставить значение 0, к которому она стремится, то получим неопределенность ви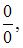да тогда

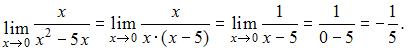
ЗАДАНИЕ N 3
Тема: Раскрытие неопределенности вида "ноль на ноль"

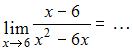
Решение:
Если вместо переменной 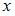поставить значение 6, к которому она стремится, то получим неопределенность вида 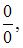тогда

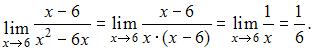
ЗАДАНИЕ N 4
Тема: Раскрытие неопределенности вида "бесконечность на бесконечность"

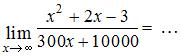
Решение:
Так как 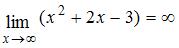и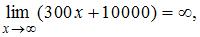
то имеет место неопределенность вида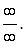
Для ее раскрытия нужно разделить каждое слагаемое числителя и знаменателя на 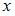. Тогда, зная, что 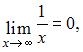получим:

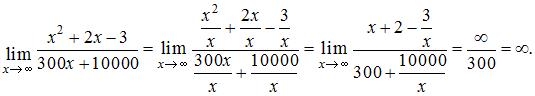
ЗАДАНИЕ N 5
Тема: Раскрытие неопределенности вида "бесконечность на бесконечность"

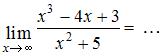
Решение:
Так как 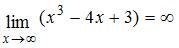и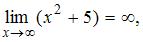
то имеет место неопределенность вида 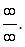Для ее раскрытия нужно разделить каждое слагаемое числителя и знаменателя на 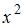. Тогда, зная, что 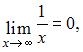получим:

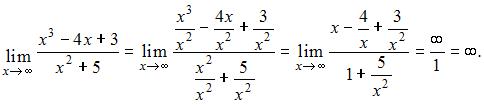
САМОСТОЯТЕЛЬНАЯ РАБОТА 20

ЗАДАНИЕ N 1
Тема: Раскрытие неопределенности вида "ноль на ноль"

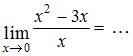
ЗАДАНИЕ N 2
Тема: Раскрытие неопределенности вида "ноль на ноль"

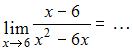
ЗАДАНИЕ N 3
Тема: Раскрытие неопределенности вида "ноль на ноль"

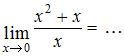
ЗАДАНИЕ N 4
Тема: Раскрытие неопределенности вида "бесконечность на бесконечность"

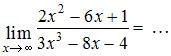
ЗАДАНИЕ N 5
Тема: Раскрытие неопределенности вида "бесконечность на бесконечность"
Предел функции 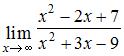равен …

ЗАДАНИЕ N 6
Тема: Раскрытие неопределенности вида "бесконечность на бесконечность"

ТЕМА 21 ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ. ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ

КОНСПЕКТ 21

ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ

Чем же замечательны замечательные пределы? Замечательность данных пределов состоит в том, что они доказаны величайшими умами знаменитых математиков, и благодарным потомкам не приходиться мучаться страшными пределами с нагромождением тригонометрических функций, логарифмов, степеней. То есть при нахождении пределов мы будем пользоваться готовыми результатами, которые доказаны теоретически.