Экспертные процедуры для принятия решений

6.1. Статистические методы экспертных оценок.

В некоторых практических задачах принятия оптимального решения альтернативы не являются, как в предыдущих примерах, математическими объектами. Для описания альтернатив и оценки последствий их принятия необходимо решить следующие задачи:

а) построить множество возможных и допустимых альтернатив;

б) сформировать набор признаков, существенных для оценки альтернатив;

в) определить критериальное пространство;

г) упорядочить альтернативы по критериям;

д) получить оценку альтернатив и принять решение о выборе.

Методы решения задач оценивания рассматриваемые в этом разделе основаны на использовании экспертных процедур, поэтому их называют методами экспертных оценок.

В тех случаях, когда объективной информации оказывается недостаточно для определения численных значений требуемого критерия при принятии решения, должны использоваться субъективные оценки, основанные на накопленном опыте, знаниях, идеях, мнениях и догадках специалистов, привлеченных к выработке субъективной оценки.

Получение объективных оценок базируется на следующих общих положениях:

1) аксиома несмещенности, которая утверждает, что мнение большинства компетентно;

2) аксиома транзитивности, утверждающая, что субъективные оценки транзитивны.

Из этого следует, что мерой качества субъективных оценок является их рассеяние.

Для качественного ознакомления с особенностями определения человеком субъективной оценки и формирования логической модели этого определения целесообразно рассмотреть ряд примеров.

Без сомнения известны методы оценки результатов в спортивных соревнованиях: гимнастике, прыжках в воду, фигурном катании и т.п. судьями-экспертами; оценки качества сортов вина, чая, духов и пр. специалистами-экспертами и т.д. Рассмотрим пример, принадлежащий Е.С. Вентцель [5]. Пусть требуется определить субъективную оценку (весовые коэффициенты) факторов 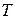- 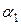и 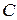- 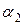критерия некоторой испытательной системы, имеющей вид 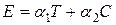, где T – время (длительность испытаний); С – стоимость испытаний; 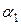, 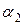– весовые коэффициенты, определяющие влияние T и С на эффективность испытаний.

Можно ожидать, что 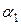и 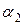будут меняться в соответствии с обстановкой, в которой проходят испытания и степенью влияния ее на личность эксперта. Так, если судьба эксперта зависит от успешности испытаний, то он будет считать, что 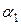<< 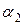, тогда для обеспечения испытаний будет закуплено большое количество оборудования, что резко увеличит их стоимость. Если непосредственной ответственности за испытания эксперт не несет, то результат оценки "веса" может быть другим. Отсюда вытекает, что субъективная оценка подвержена влиянию конъюнктуры. Если эксперт в чем-либо лично заинтересован или в данное время считается популярным определенное мнение, то экспертная оценка может отражать эту конъюнктуру. Кроме того, в процессе определения субъективной оценки могут вмешиваться те или иные авторитеты так, что оценка может быть деформирована за счет их влияния и появятся ошибки, если авторитет руководствуется предвзятым мнением. Способность эксперта противостоять воздействию конъюнктуры, назовем это объективностью, является одним из важнейших факторов, определяющих достоверность субъективной оценки.

В следующим примере предположим, что определение субъективной оценки С (см. рис.8) поручается одному эксперту Э, который базируется при определении оценки на информации, полученной из двух независимых источников A и B. Эксперт выдает оценку С только в том случае, когда оба источника дают одинаковую информацию. Будем считать, что каждый источник информации обеспечивает возможность правильной оценки проблемы с вероятностью, равной 0,7. Эта вероятность обусловлена компетентностью эксперта и его

информированностью о характере поставленной перед ним задачи.

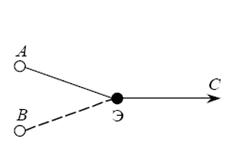
Рис. 8 Схема определения субъективной оценки одним экспертом.

Ограниченность компетентности и информированности, свойственная любому человеку, обуславливает возможность ошибки эксперта. Предположим, что он может ошибиться один раз из двухсот. Тогда вероятность правильного определения им субъективной оценки, обусловленная приведенными выше факторами, равна 0,995. Отсюда общая вероятность правильности субъективной оценки, данной экспертом равна 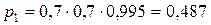, а вероятность выдачи им ошибочной оценки 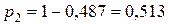. Таким образом, следующими важными факторами, определяющими правильность субъективной оценки, являются компетентность и информированность эксперта.

Таким образом, следующими важными факторами, определяющими правильность субъективной оценки, являются компетентность и информированность эксперта.

Следующий пример отличается от предыдущего только тем, что в нем определение оценки поручается четырем экспертам. В данном случае для руководства действиями экспертов назначается лицо а (см. рис. 9), которое принимает решение С, соответствующее решениям экспертов в случае их единогласия. Простота функций руководителя позволяет считать, что вероятность его ошибки равна нулю. В этом случае вероятность получения ошибочной оценки (на основе одновременного принятия ошибочной оценки всеми экспертами) определяется как .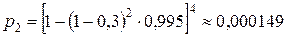

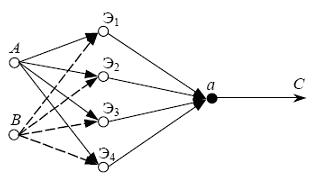
Рис. 9 Схема определения субъективной оценки четырьмя экспертами.

Очевидно, что увеличение числа экспертов резко снижает вероятность принятия ошибочного решения и, следовательно, увеличение числа экспертов, придающее оценке статический характер и допускающее ее усреднение является важным фактором, определяющим правильность субъективной оценки. Таким образом, лингвистическую модель определения субъективных оценок можно представить в виде 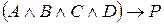, где A – информированность эксперта – совокупность представлений эксперта о задачах экспертизы, основывающаяся на внешней информации; В – компетентность эксперта – совокупность научных гипотез и конкретных идей относительно характера поведения и развития оцениваемой альтернативы; С – объективность эксперта – адекватность его представлений о факторах, определяющих характер и поведение объекта экспертизы, а также условие его развития; D – усредненность мнений эксперта, предусматривающая усреднение как по множеству экспертов, так и по множеству поставленных перед ним задач или по времени; P – имплицируемая указанными логическими предпосылками субъективная оценка.

Из вышеуказанной модели следует, что источниками ошибок при субъективной оценке могут быть:

− недостаточная информированность эксперта, связанная с неточностью формулировки задач экспертизы, неясностью и неоднозначностью используемой терминологии, недостаточной эффективностью предложенных шкал оценок; плохо составленной анкетой эксперта;

− недостаточная компетентность эксперта, определяемая слишком высокой степенью сложности задач, недостаточностью совокупности его научных гипотез и конкретных идей относительно характера и поведения объекта экспертизы, малой научной любознательностью;

− недостаточная объективность эксперта, вследствие нежелания участвовать в экспертизе, наличием прямой заинтересованности его в некоторых определенных результатах экспертизы; наличием морального давления на эксперта со стороны остановки или некоторых лиц; отсутствием материального стимулирования; отсутствием научного интереса и возможности повышения научной, технической либо иной квалификации эксперта в результате работы; большая трудоемкость заполнения анкет и т.п.;

− недостаточная усредненность мнений экспертов, связанная с ошибками анкетирования, построением процесса экспертизы; недостаточным количеством экспертов.

Таким образом, мерами для получения достоверных оценок является устранение вышеперечисленных источников ошибок. Методы реализации этих мер определяются ресурсами, находящимися в распоряжении лица, проводящего экспертизу (временем и средствами, отведенными на экспертизу, количеством экспертов и т.п.).

Формально любая экспертиза может быть разделена на три этапа: подготовка, проведение и обработка результатов.

Этап подготовки экспертизы имеет целью создание условий для получения объективных и точных оценок альтернатив. Он обычно включает в себя:

− определение задачи экспертизы;

− составление анкеты (вопросника), по которому будут опрашиваться эксперты;

− определение шкалы оценок, которой должны пользоваться эксперты;

− определение состава (списка) экспертов, привлекаемых к участию в экспертизе;

− определение порядка проведения экспертизы, показателей компетентности оценок (характеристики их точности) и метода обработки результатов.

Этап проведения экспертизы – имеет целью получение от экспертов конкретных оценок альтернатив, определенных анкетами опроса. Компетентность индивидуальных оценок обычно обеспечивается использованием итерационной процедуры с "обратной связью" на экспертов. В этом случае проведение экспертизы разделяется на несколько циклов опроса. Полученная информация, сообщаемая экспертам ("обратная связь" на экспертов) служит основанием для корректирования анкет опроса. Кроме того, эксперты могут ознакомиться с мнением своих коллег (возможна открытая дискуссия). Опрос повторяется на новом, более высоком информационном уровне. Объективность заключений достигается за счет независимости экспертов, их незаинтересованности в предмете экспертизы и отсутствия непосредственной связи между ними в ходе экспертизы. Опросы прекращаются, как только будут получены удовлетворительные значения показателей компетентности оценок.

Этап обработки результатов опроса имеет целью повышение компетентности оценки альтернативы за счет учета степени конкретной компетентности экспертов, психологических особенностей выработки индивидуальных оценок, а также социального и статистического характера процесса экспертизы.

Учет компетентности эксперта может осуществляться методом "взвешивания" индивидуальных оценок.

Учет психологических особенностей выработки человеком субъективных оценок альтернатив при их разработке может базироваться на общих положениях теории полезности, учет социальных особенностей – на теоретических положениях группового выбора.

Учет статистического характера оценок выливается в использование при их обработке в целях повышения компетентности метода усреднения.

Каждый из этих типов обработки субъективных оценок может быть реализован в соответствующей конкретной ситуации оценивания. Таких ситуаций может быть три:

− когда оценка должна быть дана одним человеком; в этом случае ее обработка проводится с использованием общих положений теории полезности;

− когда число привлеченных экспертов недостаточно для обеспечения статистической эффективности их оценок; в этом случае для получения групповой оценки следует базироваться на теории групповых решений;

− когда для формирования оценки может быть привлечено такое число экспертов, которое обеспечивает статистическую эффективность результатов экспертизы; в этом случае средством получения объективных оценок является их усреднение.

Существует три вида методов обработки экспертной информации:

- статистические;

- алгебраические;

- шкалирования.

Результаты оценок каждого эксперта можно рассматривать как реализацию некоторой случайной величины из множества допустимых оценок и применять к ним методы статистики. Статистические методы позволяют определить согласованность мнений экспертов, значимость полученных оценок и т. д., то есть качество экспертизы.

Численные оценки. Задача состоит в сопоставлении оцениваемой альтернативе одного числа

,

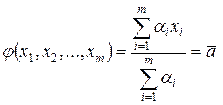(6.1)

где 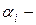вес (коэффициенты компетентности) экспертов; 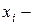числовые оценки экспертов.

При отсутствии информации о компетентности экспертов 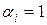, то есть выбирается средняя арифметическая оценка всех экспертов. Степенью согласованности мнений экспертов служит дисперсия:

.

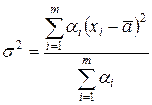(6.2)

Для повышения точности оценивания можно потребовать, чтобы каждый эксперт выставлял три оценки 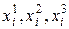- соответственно оптимистическая, наиболее вероятная и пессимистическая оценки 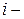ого эксперта. Эти оценки учитываются с соответствующими весами 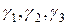определяемыми эмпирически. Тогда, единственное число, по которому оценивается альтернатива, строится как

.

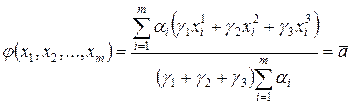(6.3)

Например, в литературе по одной из методик 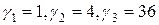, по другой 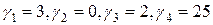, где 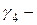степень неуверенности эксперта в своем ответе, 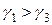, так как человек склонен к занижению оценки.

Степень согласованности экспертов определяется дисперсией

.

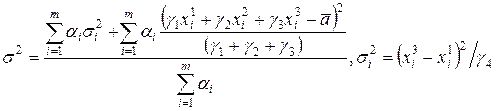(6.4)

И в первом и во втором случае экспертных оценок можно определить статистическую значимость полученных результатов. Задавшись уровнем значимости 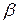укажем интервал, в который оцениваемая величина попадет с вероятностью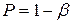

,

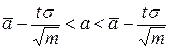(6.5)

где 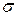определяется по формулам (6.2) или (6.4) и 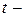коэффициент Стьюдента 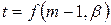, который находится по таблице.

Пример. Десять экспертов с одинаковым весом 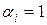оценивают величину 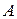. От них получены следующие результаты: 33; 35; 32,2; 34; 38; 34;37; 40; 36; 35,5.

Решение. По формулам (6.1), (6.2) получаем 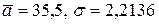. Задав 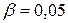, определим 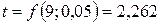. По формуле (6.5) определяем, что с вероятностью 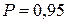величина 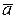попадает в интервал .

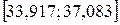Метод Делфи.

Пусть эксперты изолированы и им представлена медиана распределения неизвестной величины 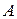, которую обозначим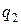 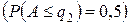и диапазон квантиле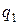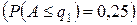й и 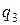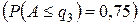. Обозначим 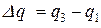. Весь интервал 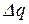значений оцениваемой величины разбиваем на 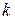интервалов числами 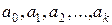. Эксперты оценивают вероятности попадания оцениваемой величины в каждый из интервалов. Обозначим вероятность попадания оцениваемой величины в 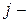ый интервал, данная 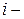м экспертом как .

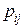На основе этих полученных значений определим суммарное мнение экспертов, с учетом их значимости, попадания в каждый из интервалов

.

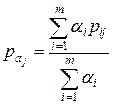(6.6)

Для полученного интервального распределения находится новая медиана 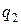и новый диапазон квантилей 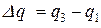, которые показывают экспертам. Затем снова эксперты делают оценки 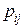и так далее до тех пор, пока диапазон 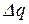не уменьшится в 1,6 раза по сравнению с первоначальным интервалом.

Ранжирование и конкордация. При строгом ранжировании результаты опроса экспертов сводятся в таблицу рангов данных 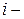м экспертом 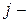му объекту (табл.25).

Таблица 25.

Эксперт	Объект
		…
			…
			…
…	…	…	…	…
			…
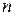
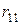
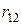
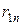
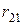
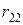
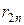
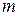
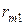
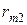
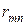
Сумма рангов			…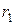

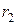
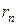
Здесь 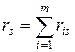. В каждой из строк одинаковых рангов в случае строгого ранжирования быть не должно.

Степень согласованности мнений экспертов при строгом ранжировании определяется при помощи коэффициента конкордации Кендалла:

,

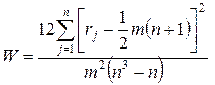(6.7)

где 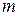- количество экспертов; 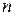- количество объектов, подлежащих экспертизе; 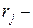ранги объектов, полученные в результате экспертизы (табл. 25).

По сути дела 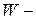это сумма квадратов отклонений рангов 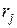от среднего значения

.

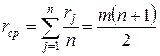(6.8)

Ясно, что этот коэффициент может меняться от 0 до 1, причем его равенство единице означает, что все эксперты дали одинаковые оценки по данному признаку или объекту, а равенство нулю означает, что связи между оценками, полученными от разных экспертов, не существует.

В случае, когда какой-либо эксперт не может установить ранговое различие между несколькими смежными факторами и присваивает им одинаковые ранги (нестрогое ранжирование), расчет коэффициента конкордации производится по формуле

,

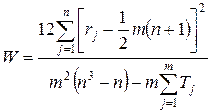(6.9)

где

,

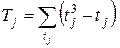(6.10)

а 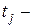число одинаковых рангов у 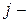ого эксперта.

Пример. Проводится экспертиза технологического процесса выплавки стали в конверторе. Задан список из шести признаков, по которым можно оценить качество полученной стали. Десять экспертов ранжировали признаки по важности (табл. 26). Необходимо оценить степень согласованности экспертов.

Таблица 26.

Признак	Номер эксперта
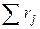
Шум
Цвет футеровки
Цвет пламени
Цвет дыма
Качество дыма
Искры

Решение. В результате вычислений получим 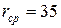; 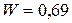. Таким образом оценка экспертов довольно согласована, так как 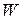ближе к единице, чем к нулю.

6.2. Метод парных сравнений.

Метод состоит в декомпозиции проблемы на все более простые составляющие части и дальнейшей обработке последовательности суждений лица, принимающего решения, по парным сравнениям.

При установлении причинно-следственных зависимостей между объектами экспертам в ряде случаев сложно выразить их численно. То есть трудно установить количественно степень влияния той или иной причины (объекта) на конкретное следствие. Особенно психологически это сложно, если таких объектов много. Вместе с тем, эксперты сравнительно легко решают задачу парного сравнения. Метод парных сравнений (точнее модификацию по Т. Саати) заключается в сравнении изучаемых объектов (альтернатив, критериев, факторов) между собой. Объекты сравниваются попарно по отношению к их воздействию («весу», или «интенсивности») на общую для них характеристику. Возникает вопрос, как получить оценку всей совокупности объектов на основе результатов парного сравнения, выполненного группой экспертов.

В отличие от ранжирования, в котором осуществляется упорядочение всех объектов, парное сравнение объектов является более простой задачей. При сравнении пары объектов возможно либо отношение строгого порядка, либо отношение эквивалентности. Отсюда следует, что парное сравнение так же, как и ранжирование, есть измерение в порядковой шкале.

Обозначим через: 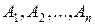основные факторы, определяющие состав объекта. Тогда для определения структуры объекта заполняется матрица парных сравнений, Если обозначить долю фактора 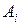через 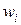(оценка, которую проставляет ЛПР или эксперт, в соответствии с выбранной шкалой), то элемент матрицы 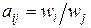, которая представлена в таблице 27. Таким образом, в предлагаемом варианте применения метода парных сравнений, определяются не величины разностей значений факторов, а их отношение, при этом очевидно .

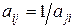Таблица 27.

Общее представление матрицы парных сравнений
			...
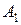
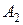
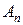
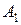
		a12		a1n
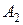
	a21			a2n
...			...
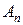
	an1	an2

Следует отметить, что матрица парных сравнений в данном случае является положительно определенной, обратно-симметричной матрицей, имеющей ранг равный 1. Особенностью обратно симметричной матрицы парных сравнений является:

a) на главной диагонали всегда должна стоять оценка равная 1 (равная важность, сравниваемых факторов, объектов, альтернатив), т.е. 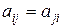при ;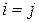

b) всегда должно выдерживаться соотношение, отвечающее условию: если при сравнении i -го объекта с j -м объектом ставится оценка 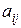, то при сравнении j -го объекта с i -м, оценка 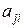должна быть обратной 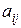, т.е. .

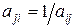Работа экспертов состоит в том, что, производя попарное сравнение факторов 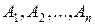, необходимо заполнить таблицу парных сравнений. Важно понять, что если 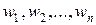неизвестны заранее, то попарные сравнения элементов производятся с использованием субъективных суждений, численно оцениваемых по шкале, а затем решается проблема нахождения соответствующей компоненты .

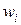Подчеркнем, что эксперт, сравнивая 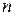факторов, реально проводит 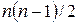сравнений.

Пример. Предположим, что необходимо провести сравнение для четырех объектов, которые сравниваются по критерию, имеющему конкретные численные значения, выраженные в условных единицах (например, критерием является длина объекта). Графическое представление параметров объектов, длина которых, выражена в условных единицах, представлено на рис. 10. Легко заметить, что наиболее важным среди рассматриваемых объектов, является объект 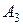(длина которого равна 9 у.е.), а наименее предпочтительным объектом является объект .

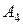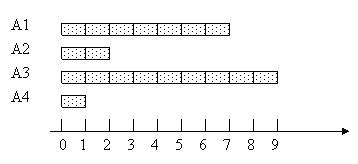
Рис. 10. Графическое представление параметров объектов,

длина которых выражена в условных единицах.

Результаты сравнения всех пар объектов удобно представлять в виде матрицы. В нашем случае имеются четыре объекта и проведено парное сравнение этих объектов по предпочтительности. Результаты сравнения представлены в виде

.

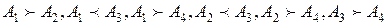(6.11)

Используя числовое представление, составим матрицу измерения результатов парных сравнений (табл. 28).

Вероятней всего рассуждения исследователя будут выглядеть так: объект 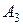имеет очень сильное превосходство над объектом 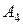, поэтому, на пересечении строки 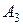и столбца 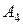можно поставить оценку равную 9. При сравнении объекта 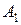с другими объектами, строку для 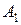можно заполнить, как это показано в таблице 28. Действительно, только объект 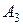имеет преобладание (не значительно длиннее) над объектом 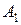, поэтому, установлена оценка равная 1/3, т.е. а₁₃ = 1/3.

Дроби, показанные в матрице (таблица 28), приведены для того, чтобы было видно, что это обратная величина сравнения двух объектов. Например, при сравнении объектов 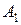и 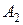будем иметь соответствующие оценки: a₁₂ = 5, а для a₂₁ = 1/5. Проведя суммирование оценок по столбцам матрицы парных сравнений, получаем абсолютные суммарные веса для каждого объекта.

Таблица 28.

Формирование матрицы на основе использования значений шкалы относительной важности
	Объект	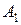Объект	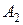Объект	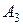Объект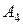
Объект	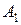		1/3
Объект	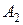1/5		1/5
Объект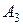
Объект	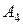1/7	1/3	1/9
Сумма	4,34	11,33	1,64	20,00

Таблица 29.

Формирование матрицы путем вычисления соотношений длин, сравниваемых объектов
	Объект	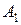Объект	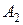Объект	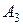Объект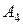
Объект	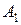	7/2	7/9	7/1
Объект	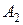2/7		2/9	2/1
Объект	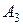9/7	9/2		9/1
Объект	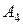1/7	1/2	1/9
Сумма	2,71	9,50	2,11	19,00

Следует отметить, что чем меньше значение суммы элементов столбца матрицы, тем выше рейтинг объекта. Имея вектор суммарных значений весов, можно предварительно сделать заключение о рейтинге объектов по заданному критерию. В примере не случайно дано количественное значение для каждой альтернативы по критерию «длина», это сделано для того, чтобы можно было реально вычислить - во сколько раз один объект превосходит другой, а затем сравнить результаты с результатами, которые были получены при вычислении относительной важности объектов по методу Т. Саати. В таблице 29 представлены результаты, полученные путем вычисления соотношений длин, сравниваемых объектов на основе заданных численных значений. Отношения длин между парами объектов в таблице 29 показаны в виде дробей, а итоговая строка таблицы отображает сумму по столбцам.

Как видно из таблицы 29, приоритеты для рассматриваемых объектов сохранились, хотя итоговые суммы по столбцам несколько отличаются от результатов, полученных в таблице 28. Естественно, перед исследователем встают два вопроса. Первый вопрос заключается – как получить относительные величины, которые характеризуют важность каждого объекта в рассматриваемой ситуации. Второй вопрос связан с определением достоверности результатов, полученных при выборе оценок относительной важности из шкалы оценок Т. Саати. Для ответа на поставленные вопросы осуществляются расчеты по определению относительных приоритетов объектов и значение согласованности оценок, которые проставил эксперт.

Для этого рассмотрим квадратную положительную матрицу порядка n, которая получена в результате парных сравнений n объектов:

,

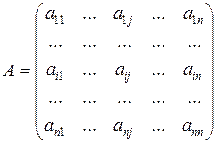(6.12)

Матрица 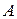называется обратно-симметричной, если для любых и j выполняется соотношение: 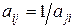. Из этого, в частности, следует, что 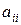= 1. Тем самым, идеальная матрица сравнений – обратно-симметричная и согласованная. При этом справедливо следующее утверждение: положительная обратно-симметричная матрица является согласованной тогда и только тогда, когда порядок матрицы и ее наибольшее собственное значение совпадают, т.е. .

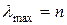Собственный вектор матрицы суждений обеспечивает упорядочение приоритетов. Часто значения собственного вектора матрицы парных сравнений называют вектором приоритетов, а собственное значение является мерой согласованности суждений. Таким образом, следующим шагом, после составления матрицы суждений (матрица парных сравнений), является вычисление вектора приоритетов. Относительная сила, величина или вероятность каждого отдельного объекта в иерархии определяется оценкой соответствующего ему элемента собственного вектора матрицы приоритетов, нормализованного к единице. Метод отыскания вектора 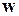основывается на одном из утверждений линейной алгебры - искомый вектор является собственным вектором матрицы парных сравнений, соответствующим максимальному собственному числу 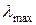. Поэтому сначала отыскивается максимальное собственное значение 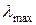, а затем собственный вектор, соответствующий максимальному собственному значению .

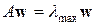Процедура определения собственных векторов матриц, которые являются весовыми коэффициентами, в соответствии со значениями которых ранжируются объекты представляет собой итерационную процедуру

,

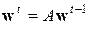(6.13)

где .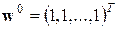

Чтобы избежать получения чрезвычайно больших весовых значений в процессе итераций компоненты вектора 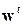на каждом шаге нормируются путем деления на величину

.

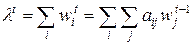(6.14)

С учетом нормирующего множителя процедура вычисления весовых коэффициентов записывается следующим образом:

,

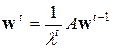(6.15)

Ее применение приводит к получению весовых коэффициентов 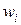в виде относительных величин, как 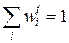. Вычислительный процесс продолжается до момента, когда весовые коэффициенты, полученные на двух соседних итерациях, будут незначительно отличаться друг от друга, т.е.

,

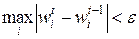(6.16)

где 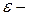достаточно малое положительное число, задающее точность расчетов.

Матрица парных сравнений неотрицательна (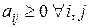) и неразложима, т. е. любыми перестановками строк и столбцов нельзя привести ее к виду

,

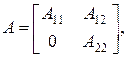(6.17)

где 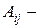квадратные подматрицы.

Если матрица 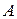неотрицательна и неразложима, то при увеличении номера итерации 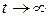величина 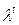сходится к максимальному собственному числу матрицы 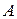, то есть

.

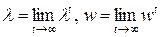(6.18)

Это утверждение следует из теоремы Перрона-Фробениуса и доказывает сходимость приведенного выше алгоритма.

Пользуясь способом приближенного вычисления собственных элементов матрицы парных сравнений, определим собственный столбец (вектор приоритетов) для рассматриваемых четырех объектов по критерию «длина».

Последовательность итераций с учетом нормирующего множителя выглядит следующим образом

,

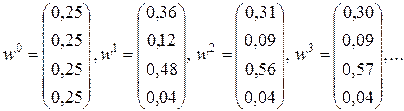(6.19)

Далее процесс продолжается до достижения заданной точности. Вектор приоритетов, вычисленный с точностью до шестого знака приведен в последнем столбце таблицы 30.

Таблица 30.

	Объект	Объект	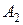Объект	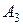Объект	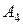Вектор приоритетов	Нормализованные оценки вектора приоритета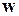
Объект	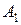		1/3		1,848148	0,302228
Объект	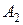1/5		1/5		0,588566	0,096248
Объект	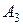				3,408658	0,557419
Объект	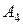1/7	1/3	1/9		0,269702	0,044104
Сумма	4,3429	11,3333	1,6444	20,0000	6,115074

Сравним полученный вектор приоритетов с соответствующим вектором, когда матрица парных сравнений составлена на основе реальных соотношений длин, полученных при осуществлении операции деления длины одного объекта на длину другого объекта (таблице 29). Например, при выяснении, на сколько объект 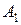превосходит объект 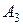, необходимо выполнить простое деление, т.е. a₁₃ = 7 / 9 = 0,778.

Вычисления вектора приоритетов проведем аналогично предыдущему случаю. Результаты вычислений представлены в таблице 31.

Таблица 31.

	Объект	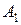Объект	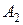Объект	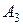Объект	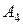Вектор приоритетов	Нормализованные оценки вектора приоритета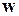
Объект	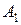1,000	3,500	0,778	7,000	2,089322	0,368421
Объект	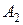0,286	1,000	0,222	2,000	0,596949	0,105263
Объект	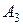1,286	4,500	1,000	9,000	2,686271	0,473684
Объект	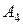0,143	0,500	0,111	1,000	0,298475	0,052632
Сумма	2,7143	9,5000	2,1111	19,0000	5,671017

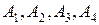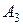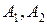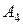Сумма всех нормализованных элементов полученного собственного столбца (его называют вектором приоритетов) равна 1. Он позволяет подвести итог проведенному анализу таблицы сравнений, среди рассматриваемых объектов . В обоих случаях, как и следовало ожидать, наивысший приоритет имеет объект , затем идут объекты и соответственно. Расчеты итоговых сумм оценок относительной важности для рассматриваемого примера приведены в таблице 32. Вариант 1 соответствует процедуре установления относительной важности объектов по методу Т. Саати, вариант 2 отражает установление приоритетов объектов вычислением длины одного объекта на длину другого объекта. При анализе таблицы видны некоторые расхождения в окончательных результатах. Это расхождение связано с различным оцениванием на первичном этапе при составлении матрицы парных сравнений.

Таблица 32.

	Объект	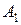Объект	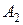Объект	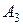Объект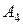
Вектор приоритетов с оценками по шкале Т.Саати (вариант 1)	0,302228	0,096248	0,557419	0,044104
Вектор приоритетов с оценками, на основе прямого деления длин (вариант 2)	0,368421	0,105263	0,473684	0,052632