 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Упражнения. 1. В 4-тонный самолет загружаются предметы трех наименований вес которых и прибыль (в тысячах рублей) от перевозки одного предмета имеют следующие значения
|
|
К п. 2.2.1
1. В 4-тонный самолет загружаются предметы трех наименований вес которых 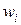 и прибыль (в тысячах рублей)
и прибыль (в тысячах рублей) 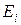 от перевозки одного предмета имеют следующие значения:
от перевозки одного предмета имеют следующие значения: 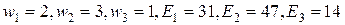 . Как необходимо загрузить самолет, чтобы получить максимальную прибыль?
. Как необходимо загрузить самолет, чтобы получить максимальную прибыль?
2. Решите задачу о загрузке из примера 1 для каждого из следующих случаев:
a) Общий вес 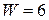 ,
, 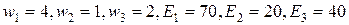 ;
;
b) Общий вес 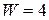 ,
, 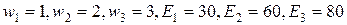 .
.
3. Шериф округа Вашингтон баллотируется на следующий срок. Денежные средства на предвыборную кампанию составляют примерно 10 000 долларов. Хотя комитет по переизбранию хотел бы провести кампанию во всех пяти избирательных участках округа, ограниченность денежных средств предписывает действовать по-другому. Приведенная ниже таблица содержит данные
о числе избирателей и денежных средствах, необходимых для проведения
успешной кампании по каждому избирательному участку. Каждый участок
может либо использовать все предназначенные деньги, либо вовсе их не использовать. Как следует распределить денежные средства?
| Участок | Число избирателей | Необходимые средства (долл.) |
К п. 2.2.2.
1. Компания производит специальные вытяжки, которые используются в домашних каминах в период с декабря по март. В начале отопительного сезона спрос на эту продукцию низкий, в середине сезона он достигает своего пика и уменьшается к концу сезона. Учитывая популярность продукции, компания может использовать сверхурочные работы для удовлетворения спроса на свою продукцию. Следующая таблица содержит данные о производственных мощностях компании и объемах спроса на протяжении четырех месяцев.
| Возможности производства | |||
| Месяц | Обычный режим работы (единицы) | Сверхурочные (единицы) | Спрос (единицы) |
Стоимость производства единицы продукции равна 6 долл. в условиях обычного режима работы и 9 долл. при сверхурочных работах. Стоимость хранения единицы продукции на протяжении месяца равна 0,10 долл. Чтобы гарантировать допустимое решение при отсутствии дефицита, требуется, чтобы предложение продукции (возможности производства плюс запас) к началу каждого месяца, по меньшей мере, равнялось спросу. Требуется так организовать производство, чтобы суммарные затраты на производство и хранение были минимальными.
К п. 2.2.3.
1. Решите задачу при следующих минимальных потребностях в рабочей силе:
а) 
б) 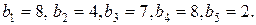
2. Пусть в примере каждому уволенному рабочему выплачивается выходное пособие в размере 100 долл. Найдите оптимальное решение задачи.
3. Туристическое агентство организовывает недельные поездки в Египет. В соответствии с договором на ближайшие четыре недели агентство должно обеспечить туристические группы арендными автомобилями в количестве семь, четыре, семь и восемь штук соответственно. Агентство заключает договор с местным дилером по прокату автомобилей. Дилер назначает арендную плату за один автомобиль 220 долл. в неделю плюс 500 долл. за любую арендную сделку. Агентство, однако, может не возвращать арендованные автомобили в конце недели, и в этом случае оно должно будет платить только арендную плату в 220 долларов. Каково оптимальное решение проблемы, связанной с арендой автомобилей?
4. Компания на следующие четыре года заключила контракт на поставку авиационных двигателей, по 4 двигателя в год. Доступные производственные мощности и стоимость производства меняются от года к году. Компания может изготовить пять двигателей за 1-й год, шесть – за 2-й, три – за 3-й и пять – за 4-й. Стоимость производства одного двигателя на протяжении следующих четырех лет равна соответственно 300 000, 330 000, 350 000 и 420 000 долл. В течение года компания может произвести больше 458 двигателей, чем необходимо, но в этом случае двигатели должны надлежащим образом храниться до их отгрузки потребителю. Стоимость хранения одного двигателя также меняется от года к году и оценивается в 20 000 долл. для первого года, 30 000 долл. – для второго, 40 000 долл. – для третьего и 50 000 – для четвертого. В начале первого года компания имеет один двигатель, готовый к отгрузке. Разработайте оптимальный план производства двигателей.
К п. 3.1.1.
1. Пусть для задачи выбора университета Мартином и Джейн установлены следующие значения весовых коэффициентов:

Основываясь на этой информации, оцените с помощью комбинированных весов каждый из трех университетов.
2. Отдел кадров фирмы сузил поиск будущего сотрудника до трех кандидатур:
Николай (Н), Дмитрий (Д) и Михаил (М). Конечный отбор основан на трех критериях: собеседование (С), опыт работы (О) и рекомендации (Р). Отдел кадров использует матрицу А (приведенную ниже) для сравнения трех критериев. После проведенного собеседования с тремя претендентами, сбора данных, относящихся к опыту их работы и рекомендациям, построены матрицы 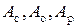 . Какого из трех кандидатов следует принять на работу?
. Какого из трех кандидатов следует принять на работу?
 , ,
|
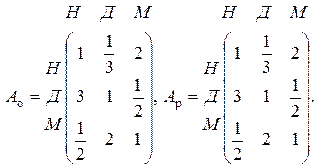 , ,
|
3. Решив купить автомобиль, человек сузил свой выбор до трех моделей: 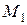 ,
, 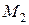 и
и 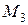 . Факторами, влияющими на его решение, являются: стоимость автомобиля (С), стоимость обслуживания (О), стоимость поездки по городу (Г) и сельской местности (М). Следующая таблица содержит необходимые данные, соответствующие трехгодичному сроку эксплуатации автомобиля.
. Факторами, влияющими на его решение, являются: стоимость автомобиля (С), стоимость обслуживания (О), стоимость поездки по городу (Г) и сельской местности (М). Следующая таблица содержит необходимые данные, соответствующие трехгодичному сроку эксплуатации автомобиля.
| Модель автомобиля | С (долл.) | О (долл.) | Г (долл.) | М (долл.) |
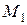
| 6 000 | |||
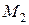
| 8 000 | |||
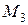
| 10 000 |
Используйте указанные стоимости для построения матриц сравнений и модель автомобиля, которую следует выбрать.
К п. 3.1.2.
1. Электроэнергетическая компания использует парк из 20 грузовых автомобилей для обслуживания электрической сети. Компания планирует периодический профилактический ремонт автомобилей. Вероятность поломки автомобиля в первый месяц равна нулю, во второй месяц — 0,03 и увеличивается на 0,01 для каждого последующего месяца, по десятый включительно. Начиная с одиннадцатого месяца и далее, вероятность поломки сохраняется постоянной на уровне 0,13. Случайная поломка одного грузового автомобиля обходится компании в 200 долл., а планируемый профилактический ремонт в 75 долл. Компания хочет определить оптимальный период (в месяцах) между планируемыми профилактическими ремонтами.
a) Постройте соответствующее дерево решений.
b) Определите оптимальную длину цикла для профилактического ремонта.
К п. 3.1.3.
1. Хенк — прилежный студент, который обычно получает хорошие отметки благодаря, в частности, тому, что имеет возможность повторить материал в ночь перед экзаменом. Перед завтрашним экзаменом Хенк столкнулся с небольшой проблемой. Его сокурсники организовали на всю ночь вечеринку, в которой он хочет участвовать. Хенк имеет три альтернативы:
 участвовать в вечеринке всю ночь,
участвовать в вечеринке всю ночь,
 половину ночи участвовать в вечеринке, а половину — учиться,
половину ночи участвовать в вечеринке, а половину — учиться,
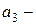 учиться всю ночь.
учиться всю ночь.
Профессор, принимающий завтрашний экзамен, непредсказуем, и экзамен может быть легким (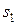 ), средним (
), средним (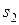 ) или трудным (
) или трудным (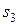 ). В зависимости от сложности экзамена и времени, затраченного Хенком на повторение, можно
). В зависимости от сложности экзамена и времени, затраченного Хенком на повторение, можно
ожидать следующие экзаменационные баллы.
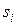

| 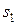
| 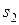
| 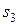
|
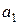
| |||
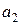
| |||

|
a) Порекомендуйте Хенку, какой выбор он должен сделать (основываясь на каждом из четырех критериев принятия решений в условиях неопределенности).
b) Предположим, что Хенк более заинтересован в оценке (в буквенном выражении), которую он получит на экзамене. Буквенным оценкам от А до
D, означающим сдачу экзамена, соответствует 90, 80, 70 и 60 баллов.
Иначе при числе баллов ниже 60 студент получает оценку F, которая свидетельствует о том, что экзамен не сдан. Изменит ли такое отношение к оценкам выбор Хенка?
К п. 3.2.
1. Где строить? Две конкурирующие крупные торговые фирмы 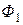 и
и  , планируют построить в одном из четырех небольших городов
, планируют построить в одном из четырех небольших городов 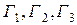 и
и  , лежащих вдоль автомагистрали, по одному универсаму. Взаимное расположение городов, расстояние между ними и численность населения показаны на следующей схеме.
, лежащих вдоль автомагистрали, по одному универсаму. Взаимное расположение городов, расстояние между ними и численность населения показаны на следующей схеме.
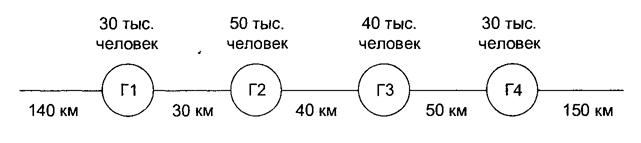
Распределение оборота, получаемого каждой фирмой, определяется численностью населения городов, а также степенью удаленности универсамов от места жительства потенциальных покупателей. Специально проведенное исследование показало, что торговый оборот в универсамах будет распределяться между фирмами так, как это показано в следующей таблице.
| Условия | Распределение оборота между фирмами, % | |

| 
| |
Универсам фирмы 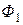 расположен к городу ближе универсама фирмы расположен к городу ближе универсама фирмы 
| ||
| Универсамы обеих фирм расположены на одинаковом расстоянии от города | ||
Универсам фирмы 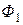 расположен от города дальше универсама фирмы расположен от города дальше универсама фирмы 
|
Например, если универсам фирмы 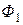 расположен к городу
расположен к городу 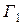 ближе универсама фирмы
ближе универсама фирмы  , то оборот фирм от покупок, сделанных жителями данного города, распределится следующим образом: 75% получит
, то оборот фирм от покупок, сделанных жителями данного города, распределится следующим образом: 75% получит 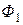 , остальное –
, остальное –  . Представьте описанную ситуацию, как игру двух лиц и определите, в каких городах целесообразно фирмам построить свои универсамы.
. Представьте описанную ситуацию, как игру двух лиц и определите, в каких городах целесообразно фирмам построить свои универсамы.
2. Двухпальцевая игра мора. Каждый игрок показывает один или два пальца и называет число пальцев, которое, по его мнению, показал его противник (ни один из игроков не видит, какое число пальцев на самом деле показывает его противник). Если один из игроков угадывает правильно, он выигрывает сумму, равную сумме числа пальцев, показанных им и его противником. В противном случае (если никто не угадывает), – ничья. Если оба угадали, то оба платят друг другу одинаковую сумму, в результате также ничья.
Ответьте на следующие вопросы.
а) Существует ли в данной игре седловая точка в чистых стратегиях?
б) Кто из игроков в среднем выигрывает и сколько?
в) Как часто игрок 1 должен говорить, что его противник показал два пальца?
г) Как часто игрок 2 должен показывать 1 палец?
3. Указать значение элемента матрицы игры в седловой точке:
| Ситуации игрока 2 | Ситуации игрока 1 | |||
| -5 | ||||
Возможные ответы: 1) 6; 2) 8; 3) 15; 4) 25; 5) седловая точка отсутствует.
4. Известный актер обдумывает, где бы ему провести в текущем году отпуск. Он рассматривает 6 возможных вариантов: Монте-Карло (МК), Гавайские острова (Г), Багамские острова (Б), Канарские острова (К), Сочи (С), озеро Байкал (ОБ). Единственный критерий для выбора места отдыха — это стремление избежать журналистов, которые могут испортить ему отдых. Если они его «выследят», отдых будет испорчен (полезность равна 0). В противном случае, все будет, как запланировано (полезность равна 1). Вследствие различных географических условий, актера можно обнаружить на территории, где находятся и актер и журналисты, с определенной (известной) вероятностью: в Монте-Карло с вероятностью 0,34; на Гавайских островах с вероятностью 0,12; на Багамских островах с вероятностью 0,16; на Канарских островах с вероятностью 0,4; в Сочи с вероятностью 0,5; и на озере Байкал с вероятностью 0,2.
Опишите данную ситуацию, как игру двух лиц с нулевой суммой (актер — это игрок 1). Вычислите цену игры и определите минимаксные стратегии обоих игроков.
Ответьте на вопросы:
а) Чему равна максимальная ожидаемая полезность отпуска актера?
б) С какой вероятностью актер поедет в отпуск на Байкал?
в) Чему равна верхняя цена игры?
г) В каком из мест наиболее вероятно будет отдыхать актер?
К п. 7.1.
1. В каждой из следующих ситуаций определите понятия клиента и сервиса (средства обслуживания).
a) Самолеты, прибывающие в аэропорт.
b) Стоянка такси.
c) Обрабатывающие инструменты в цехе механической обработки.
d) Письма, обрабатываемые в почтовом отделении.
e) Регистрация на учебу в университете.
f) Судебные дела судьи.
g) Процесс контроля в супермаркете.
h) Обслуживание площадки, отведенной под автостоянку.
2. В каждой ситуации, описанной в предыдущем упражнении, определите следующее:
а) мощность источника "клиентов" (конечная или бесконечная),
б) характер поступающих "клиентов" (индивидуальные или групповые),
в) тип интервалов времени между последовательными поступлениями заявок (случайный или детерминированный),
г) тип времени обслуживания,
д) вместимость очереди (конечная или бесконечная) и
е) дисциплину очереди.
3. Проанализируйте описанные ниже ситуации и опишите их с помощью моделей массового обслуживания. В каждом случае определите "клиентов", сервисы, дисциплину очереди, время обслуживания, максимальную длину очереди, а также источник "клиентов".
a) В мастерскую поступают заказы на выполнение работ. При их приемке диспетчер указывает, является заказ срочным или обычным. Для выполнения некоторых заказов требуется использовать один из нескольких одинаковых станков, которыми располагает мастерская. Остальные заказы выполняются на двухэтапной производственной линии; их в мастерской имеется две. В каждой из двух групп оборудования мастерской один станок предназначается для выполнения срочных работ.
b) Заявки, поступающие на некоторое обслуживающее устройство, выполняются в порядке их поступления. Выполненные заказы до момента их отправки клиентам складируются в специальном помещении зоны готовой продукции, которое имеет ограниченную вместимость.
с) Режущими инструментами различные станки обеспечиваются из центрального инструментального склада. При выходе станка из строя вызывается механик из централизованной службы ремонта. Станки, выполняющие срочные заказы, всегда имеют преимущество как при получении нового инструмента со склада, так и при выполнении ремонтных работ.
К п. 7.2.
1. Объясните связь между интенсивностью поступления заявок на обслуживание 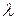 и средним временем между последовательными их поступлениями. В каких единицах измеряется каждая из этих величин?
и средним временем между последовательными их поступлениями. В каких единицах измеряется каждая из этих величин?
2. В каждом из следующих случаев определите среднюю интенсивность (в час) поступлений заявок на обслуживание 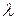 и среднее время между их последовательными поступлениями.
и среднее время между их последовательными поступлениями.
a) Каждые 10 минут происходит одно поступление.
b) Каждые 6 минут происходит два поступления.
c) Число поступлений за 30 минут равно 10.
d) Средний интервал между последовательными поступлениями равен 0,5 часа.
3. Время между последовательными поступлениями клиентов в Управление департамента государственных сборов распределено по экспоненциальному закону со средним значением 0,05 часа. Управление начинает работу в 8:00.
a) Определите плотность вероятности экспоненциального распределения, описывающего время между последовательными поступлениями клиентов.
b) Определите вероятность того, что до 8:15 в управлении клиентов не будет.
c) Сейчас 8:35. Последний клиент прибыл в управление в 8:26. Какова вероятность того, что следующий клиент прибудет до 8:38? Какова вероятность того, что следующего клиента не будет до 8:40?
d) Чему равно среднее число посетителей, которые прибудут в управление от 8:10 до 8:45?
4. Помогите управляющему нового ресторана быстрого питания описать количественно процесс поступления посетителей, оценивая долю интервалов времени между их приходами, которые будут
а) меньше двух минут,
б) больше трех минут и
в) от двух до трех минут.
Интенсивность поступления посетителей в рестораны подобного типа равна 35 клиентов в час. Время между приходами последовательных посетителей распределено по экспоненциальному закону.
5. Официанты 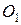 и
и 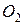 ресторана быстрого питания в ожидании посетителей заняты следующей игрой: если в течение одной минуты в ресторан не прибудет ни один посетитель,
ресторана быстрого питания в ожидании посетителей заняты следующей игрой: если в течение одной минуты в ресторан не прибудет ни один посетитель, 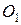 , платит 2 цента
, платит 2 цента 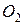 , в противном случае 2 цента от
, в противном случае 2 цента от 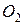 получает
получает 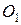 . Требуется вычислить средний выигрыш официанта
. Требуется вычислить средний выигрыш официанта 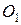 за восьмичасовой период. Время между последовательными прибытиями посетителей распределено по экспоненциальному закону со средним значением 1,5 мин.
за восьмичасовой период. Время между последовательными прибытиями посетителей распределено по экспоненциальному закону со средним значением 1,5 мин.
6. Посетитель ресторана быстрого питания, который приходит в пределах четырехминутного интервала после предыдущего посетителя, обслуживается без очереди. Если же время между последовательными приходами посетителей составляет от 4 до 5 мин., время ожидания будет около 1 мин. Если же время между последовательными приходами посетителей больше 5 мин., время ожидания составляет около 2 мин. Время между последовательными приходами посетителей является случайной величиной, распределенной по экспоненциальному закону со средним значением 6 мин.
a) Определите вероятность того, что прибывающий посетитель не будет
ожидать в очереди.
b) Определите среднее время ожидания для прибывающего посетителя.
К п.7.3.
1. Каждое утро в холодильник небольшой мастерской помещается два ящика (по 24 банки) безалкогольных напитков для десяти работников. Они могут утолять свою жажду в любой момент на протяжении восьмичасового рабочего дня (с 8:00 до 16:00). Процесс потребления напитков является случайным (в соответствии с распределением Пуассона), но известно, что в среднем каждый работник употребляет примерно 2 банки в день. Какова вероятность того, что запас напитков, исчерпается к полудню? К моменту закрытия мастерской?
2. Студент-первокурсник ежемесячно получает от родителей банковский депозит на 100 долл. для покрытия текущих расходов. Получение студентом денег чеками по 20 долл. каждый на протяжении месяца происходит случайным образом в соответствии с экспоненциальным законом со средним значением 1 раз в неделю. Определите вероятность того, что к концу месяца (т.е. к концу четвертой недели) у студента не будет денег на текущие расходы.
3. На складе находится 80 единиц продукции, которая изымается в соответствии с распределением Пуассона с интенсивностью 5 единиц в день. Требуется определить следующее.
a) Вероятность того, что за два дня из склада будет изъято 10 единиц продукции.
b) Вероятность того, что к концу четвертого дня на складе не останется ни одной единицы продукции.
c) Среднее количество изъятых единиц продукции на протяжении четырех дней.
4. Объем спроса на изделие является случайной величиной, распределенной по закону Пуассона со средним значением 3 единицы в день. Максимальная вместимость склада равна 25 единицам. Склад полностью заполняется каждый понедельник сразу же после получения нового заказа. Объем заказа зависит от количества изделий, оставшихся к концу недели в субботу (воскресенье — выходной день). Требуется определить следующие параметры.
a) Средний недельный объем заказа.
b) Вероятность отсутствия запаса утром в пятницу.
c) Вероятность того, что недельный объем заказа превысит 10 единиц.
5. Докажите, что в модели чистой гибели распределение времени между удалениями (подчиняющимися усеченному распределению Пуассона) клиентов из системы является экспоненциальным с математическим ожиданием 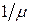 единиц времени.
единиц времени.
К п. 7.6.
1. Студент университета Джон иногда подрабатывает, чтобы улучшить свое материальное положение. Интервал времени между последовательными поступлениями заявок на работу является экспоненциально распределенной случайной величиной со средним значением пять дней. Время, необходимое для выполнения работы, также является экспоненциально распределенной слу-
чайной величиной со средним значением четыре дня.
a) Какова вероятность того, что Джон будет без работы?
b) Если за каждую работу Джон получает примерно 50 долл., то каков его
среднемесячный заработок?
с) Если в конце семестра Джон решает передоверить невыполненные работы
другому лицу по 40 долл. за каждую работу, то каково среднее значение
суммы, которую должен уплатить Джон?
К п. 7.7.
1. Определите минимальное количество сервисов в каждой из следующих ситуаций (предполагается пуассоновское распределение поступления клиентов и обслуживания), которое гарантирует стационарный режим работы системы массового обслуживания (в этом случае длина очереди не будет неограниченно возрастать).
a) Клиенты прибывают каждые 5 мин., а обслуживаются с интенсивностью 10 клиентов в час.
b) Среднее время между последовательными прибытиями клиентов равняется 2 мин., а среднее время обслуживания – 6 мин.
c) Интенсивность входного потока – 30 клиентов в час, а интенсивность обслуживания одним сервисом – 40 клиентов в час.
При изучении курса «Основы системного анализа» студент выполняет 1 контрольную работу и 1 курсовую работу. Для этого он должен изучить методы решения задач динамического программирования, теории игр, экспертные методы принятия решений, принципы функционирования систем массового обслуживания и уметь применять их для решения практических задач.
Требования к оформлению курсовой работы излагаются преподавателем на установочных лекциях по данному предмету.
Дата публикования: 2014-11-02; Прочитано: 2875 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
