Задачи теории принятия решений и системный подход

Задачи принятия решений часто отождествляются с задача­ми выбора, являющимися одними из самых распространенных задач, с которыми человек сталкивается в своей деятельности. В повседневной жизни в силу повторяемости, стереотипности ситуа­ций человек принимает решение, почти не задумываясь, часто интуитивно или по аналогии. Лучший вариант обычно на­ходится без какого-то особого анализа.

В более сложных и соответственно более редких, уникальных ситуациях, например при выборе места отдыха, учебы или ра­боты, покупке квартиры или дорогостоящей вещи (автомобиля, мебели и т.д.), голосовании за того или иного кандидата или партию, человек более тщательно подходит к своему выбору. Прежде чем принять решение, он старается детально рассмот­реть, оценить и сопоставить различные варианты, учесть разные точки зрения.

Еще более сложные задачи выбора возникают в професси­ональной деятельности каждого руководителя, ученого, кон­структора, врача, экономиста, финансиста, бизнесмена, воена­чальника.

Теория принятия решения как самостоятельное научное на­правление стала складываться в середине ХХ века в рамках мето­дологии системного анализа (СА), хотя самые первые работы по ис­следованию голосования как способа коллективного выбора по­явились еще в конце XVII века. Основное назначение теории при­нятия решений состоит в разработке методов и средств, позволяющих одному человеку или группе лиц формулировать мно­жество возможных вариантов решения проблемы. Затем, сравнивать их между собой, находить среди них лучшие или допустимые вариан­ты, которые удовлетворяют тем или иным требованиям (ограни­чениям), и, при необходимости, объяснить сделанный выбор.

Без преувеличения можно сказать, что необходимость обос­нования выбора присутствует во всех сферах человеческой де­ятельности. Обоснованный выбор особенно важен в управлении организационными и техническими системами. Однако одного искусства в принятии решений в современ­ных условиях мало.

Изучением того, как человек принимает решения, и созда­нием методов выбора занимаются многие научные дисциплины, которые возникли и исторически развивались независимо друг от друга. К ним относятся такие дисциплины, как: теория принятия решений, систем­ный анализ, теория исследования операций, теория игр, экспертные методы принятия решения и др. Эти дисциплины с разных точек зрения анализируют меха­низмы, процессы и правила выбора оптимального решения применительно к объектам различной природы и в различных условиях их существования. Все вместе они образуют много дисциплинарную науку, помога­ющую человеку сделать обоснованный выбор.

Теория принятия решений может оказать существенную по­мощь в анализе и решении сложных проблем, но лишь тогда, когда ее методологические и математические средства приме­няются «правильно», соответственно их возможностям, не пре­увеличивая и не умаляя их роли в процессе нахождения реше­ния. Основным инструментом для принятия оптимального решения, как следует из предыдущего, является математическое моделирование. Сейчас принято называть использование математического моделирования в задачах принятия решений исследованием операций (ИО).

Теорию принятия решений, поэтому, правильнее было бы назвать теорией поиска и обоснованного выбора наиболее пред­почтительных для человека вариантов решения проблемы.

Предположим, что в соответствии с деловыми обязательствами вам необходимо в течение пяти недель пять раз посетить город 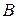(а живете вы в городе 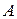). Вы должны быть в городе 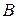в понедельник первой недели и окончательно возвратиться в город 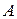в среду пятой недели. Билет из города 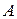в город 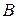и обратно стоит 4000 руб., однако вы можете получить 20% скидки от стоимости билетов, если вылет придется на конец недели. Кроме того, следует учесть, что стоимость билета только в одну сторону равна 75% от стоимости заказного билета. Вы, естественно, хотите минимизировать стоимость перелетов. Как это сделать?

Описанную ситуацию можно рассматривать как задачу принятия решений, где для поиска оптимального решения требуется определить три основных компонента.

1. Что в данном случае считать альтернативными решениями?

2. Каким ограничениям должно удовлетворять возможное решение?

3. По какому критерию должны отбираться альтернативные решения?

В нашей задаче возможны следующие альтернативы.

1. Покупка пяти заказных билетов 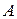- - 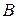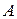(т.е. из города 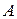в город 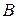и обратно).

2. Покупка одного билета в одну сторону 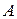- 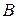, четырех билетов 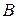- - 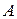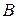, захватывающих конец недели, и одного "однонаправленного" билета - .

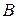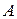3. Покупка билета 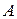- - 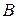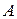для первой недели, причем между датами вылетов должен быть понедельник; для последней недели приобретение билета 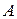- - 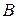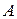, между датами которого должна быть среда, причем первый и последний билеты должны захватывать последние дни недели; покупка четырех билетов 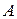- - 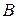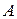, между датами которых также есть последние дни недели. Ограничением в данной задаче являются дни прибытия: понедельник первой недели и среда пятой.

В данном случае естественным критерием для оценки возможных альтернатив является цена билетов. Альтернатива, обеспечивающая наименьшую стоимость билетов, будет наилучшей. В данном случае имеем следующие варианты.

Альтернатива 1: стоимость билетов = 5^.4000 = 20000 руб.

Альтернатива 2: стоимость билетов = 0,75^.4000 + 4^.0,8^. 4000 + 0,75^.4000 = 18000 руб.

Альтернатива 3: стоимость билетов = 5^.0,8^.4000 = 16000 руб.

Очевидно, что наилучшей является третья альтернатива.

Приведенный пример показывает основные принципиальные составляющие ИО, а именно альтернативы, ограничения и критерий отбора альтернатив. Но в различных ситуациях эти составляющие могут весьма отличаться от аналогичных составляющих других моделей.

На практике реализация методов ИО должна включать следующие этапы.

1. Формализация исходной проблемы.

2. Построение математической модели.

3. Решение модели.

4. Проверка адекватности модели.

5. Реализация решения.

Из всех пяти приведенных этапов только третий, решение модели, достаточно точно определен и наиболее прост для реализации в рамках методологии ИО, поскольку действия на этом этапе основываются на точной математической теории. Выполнение остальных этапов в значительной мере является искусством, а не наукой. Поэтому мы не можем точно описать эти процедуры.

Формализация проблемы требует исследования той предметной области, где возникла рассматриваемая проблема. Это начальный этап работы любой команды аналитиков ИО. В результате такого исследования должны быть получены следующие три принципиальных элемента решаемой задачи: 1) описание возможных альтернативных решений, 2) определение целевой функции, 3) построение системы ограничений, налагаемых на возможные решения.

Построение математической модели означает перевод формализованной задачи, описание которой получено на предыдущем этапе, на четкий язык математических отношений. Если получена одна из стандартных математических моделей, например, модель линейного программирования, то решение обычно достигается путем использования существующих алгоритмов. Если же результирующая модель очень сложная и не приводится к какому-либо стандартному типу моделей, то команда ИО может либо упростить ее, либо применить эвристический подход, либо использовать имитационное моделирование. В некоторых случаях комбинация математической, имитационной и эвристической моделей может привести к решению исходной проблемы.

Решение модели, как уже упоминалось, – наиболее простой из всех этапов реализации методов исследования операций, так как здесь используются известные алгоритмы оптимизации. Важным аспектом этого этапа является анализ чувствительности полученного решения. Это подразумевает получение дополнительной информации о поведении "оптимального" решения при изменении некоторых параметров модели. Анализ чувствительности особенно необходим, когда невозможно точно оценить параметры модели. В этом случае важно изучить поведение оптимального решения в окрестности первоначальных оценок параметров модели.

Проверка адекватности модели предполагает проверку ее правильности, т.е. определения того, соответствует ли поведение модели в конкретных ситуациях поведению исходной реальной системы. Но сначала команда аналитиков ИО должна удостовериться, что модель не содержит "сюрпризов". Другими словами, надо убедиться, что решение, полученное в рамках построенной модели, имеет смысл и интуитивно приемлемо. Формальным общепринятым методом проверки адекватности модели является сравнение полученного решения (поведение модели) с известными ранее решениями или поведением реальной системы. Модель считается адекватной, если при определенных начальных условиях ее поведение совпадает с поведением исходной системы при тех же начальных условиях. Конечно, это не гарантирует, что при других начальных условиях поведение модели будет совпадать с поведением реальной системы. В некоторых случаях в силу разных причин невозможно прямое сравнение модели с реальной системой или сравнение решений, полученных в рамках этой модели, с известными решениями (например, из-за отсутствия таких данных). В такой ситуации для проверки адекватности математической модели можно использовать имитационное моделирование, т.е. сравнивать поведение математической и имитационной моделей.

Реализация решения подразумевает перевод результатов решения модели в рекомендации, представленные в форме, понятной для лиц, принимающих решения, т.е. заказчиков. Бремя этой непростой задачи ложится непосредственно на плечи команды аналитиков ИО.

Задачи исследования операций можно разделить на классы: поисковые, распределительные, управления запасами, массового обслуживания, календарного планирования, состязательные задачи.

Классы задач и методы их решения представлены в таблице 1.1.

Таблица 1.1.

Классы задач	Методы решения
Поисковые	Нелинейное программирование
Распределительные	Линейное программирование
Управление запасами	Теория управление запасами
Массовое обслуживание	Теория массового обслуживания
Календарное планирование	Теория расписания
Состязательные задачи	Теория игр

Существуют две противоположные точки зрения на роль формальных методов при решении практических проблем выбо­ра. Люди, профессионально не владеющие математическими ме­тодами, нередко считают, что любая проблема может быть фор­мально переведена на язык математики и потом решена ее сред­ствами. Другие полностью отвергают такие возможности. Дей­ствительность же гораздо сложнее этих крайних утверждений.

Любые ситуации, требующие принятия решения, содержат, как правило, большое число неопределенных факторов, которые оказывают влияние, как на формальную постановку задачи, так и на средства ее решения. Эти неопределенные факторы можно в самом общем виде разбить на три группы.

Прежде всего, это так называемая неопределенность приро­ды, т. е. факторы людям попросту неизвестные или от них не за­висящие. Затем — неопределенность человека, который может вести себя непоследовательно, противоречиво, допускать ошиб­ки, зависеть от других лиц (партнеров, противников и т. д.), чьи действия он не может полностью учесть или предвидеть. И, на­конец, неопределенность целей, которые могут различаться и не совпадать друг с другом. Например, авиаконструкторы, проек­тируя самолет, должны учитывать его целевое назначение, за­данные показатели скорости, грузоподъемности и дальности по­лета, условия безопасности и комфортности для экипажа и пас­сажиров, факторы экономичности и технологичности производ­ства и эксплуатации самолета, экологические требования и мно­гие другие обстоятельства.

Ясно, что полностью свести подобные задачи с неопреде­ленностью к корректно поставленным математическим задачам нельзя в принципе. Чтобы сделать возможным их решение, надо как-то ограничить, уменьшить или, как говорят, «снять» неопре­деленность. Для этого проводится содержательный анализ про­блемной ситуации, делаются какие-либо предположения и вво­дятся упрощения в постановку задачи. И именно средства, вхо­дящие в состав тех или иных методов принятия решений, очень часто позволяют получить дополнительную информацию, нуж­ную для формализации реальной проблемной ситуации и приве­дения ее к виду, пригодному для использования математических методов и получения приемлемого результата.

Говоря о практической применимости методов принятия ре­шений, следует особенно подчеркнуть, что должны существо­вать как объективные внешние обстоятельства, так и субъектив­ные внутренние условия, которые побуждали бы человека – ру­ководителя, ответственного за решение стоящей проблемы, спе­циалиста, аналитика — искать лучшие варианты ее решения. Без такой потребности спрос на научно обоснованные методы выбо­ра будет невелик.

1.1. Этапы принятия решений

Принятие решений не является каким-то обособленным, единовременным актом. Это процесс, протекающий во времени и состоящий из несколько этапов. Любой процесс в природе – физический, химический, социальный, мыслительный и т.д., будучи предоставленный сам себе, развивается и протекает по некоторым присущим ему закономерностям. Но на этот процесс воздействуют другие процессы, также как и сам он воздействует на них в силу всеобщей связи явлений в природе, что приводит к отклонениям от первоначального развития рассматриваемого процесса, т.е. он протекает по более сложным закономерностям.

Человек наделён сознанием, существо свободное и обречено на выбор решений, стараясь сделать всё наилучшим образом. В наиболее общем смысле теория принятия оптимальных решений представляет собой совокупность математических и численных методов, ориентированных на нахождение наилучших вариантов из множества альтернатив и позволяющих избежать их полного перебора. Ввиду того, что размерность практических задач, как правило, достаточно велика, а расчеты в соответствии с алгоритмами оптимизации требуют значительных затрат времени, то методы принятия оптимальных решений главным образом ориентированы на реализацию их с помощью ЭВМ.

Все внешние воздействия подразделяются на случайные и управляющие. Случайные воздействия являются следствием взаимодействия рассматриваемых процессов, в то время как управляющие воздействия изменяют ход того процесса, на который они направлены, в желаемом направлении. В связи с этим должен существовать некоторый орган, систематически или по мере необходимости вырабатывающий управляющие воздействия. Такой орган принято называть системой управления.

Инженерное дело теснейшим образом связано с совокупностями объектов, которые принято называть сложными системами. На первый взгляд каждая сложная система имеет уникальную организацию. Однако более детальное изучение способно выделить общее в системе команд ЭВМ, в процессах проектирования лесной машины, самолета и космического корабля.

В научно-технической литературе существует ряд терминов, имеющих отношение к исследованию сложных систем. Наиболее общий термин " теория систем " относится к всевозможным аспектам исследования систем. Ее основными частями являются

· системный анализ, который понимается как исследование проблемы принятия решения в сложной системе,

· кибернетика, которая рассматривается как наука об управлении и преобразовании информации.

Здесь следует заметить, что понятие управления не совпадает с принятием решения. Условная граница между кибернетикой и системным анализом состоит в том, что первая изучает отдельные и строго формализованные процессы, а системный анализ - совокупность процессов и процедур.

Системный анализ как дисциплина сформировался в результате возникновения необходимости исследовать и проектировать сложные системы, управлять ими в условиях неполноты информации, ограниченности ресурсов и дефицита времени. Системный анализ является дальнейшим развитием целого ряда дисциплин, таких как исследование операций, теория оптимального управления, теория принятия решений, экспертный анализ, теория организации эксплуатации систем и т.д. Для успешного решения поставленных задач системный анализ использует всю совокупность формальных и неформальных процедур. Перечисленные теоретические дисциплины являются базой и методологической основой системного анализа. Широкое распространение идей и методов системного анализа, а главное – успешное их применение на практике стало возможным только с внедрением и повсеместным использованием ЭВМ. Именно применение ЭВМ как инструмента решения сложных задач позволило перейти от построения теоретических моделей систем к широкому их практическому применению. В связи с этим Н.Н. Моисеев пишет [19], что системный анализ – это совокупность методов, основанных на использовании ЭВМ и ориентированных на исследование сложных систем – технических, экономических, экологических и т.д.

Очень близкое к термину "системный анализ" понятие - " исследование операций ", которое традиционно обозначает математическую дисциплину, охватывающую исследование математических моделей для выбора величин, оптимизирующих заданную математическую конструкцию (критерий). Системный анализ может сводиться к решению ряда задач исследования операций, но обладает свойствами, не охватываемыми этой дисциплиной. Однако в зарубежной литературе термин "исследование операций" не является чисто математическим и приближается к термину "системный анализ". Широкая опора системного анализа на исследование операций приводит к таким его математизированным разделам, как

· постановка задач принятия решения;

· описание множества альтернатив;

· исследование многокритериальных задач;

· методы решения задач оптимизации;

· обработка экспертных оценок;

· работа с макромоделями системы.

Укрупненный системный анализ состоит из этапов постановки задачи, структуризации системы, построения и исследования модели. Так как не все перечисленные этапы имеют формальный аппарат, то, следовательно, на современном уровне системный анализ не является строгим научным методом, некоторые этапы и задачи выполняются на содержательном уровне, на основе логики, здравого смысла, инженерного опыта и интуиции.

В подходе анализа систем и исследования операций можно выделить следующие пять логических элементов:

− цель или совокупность целей;

− альтернативные средства, при помощи которых можно достичь цели;

− ресурсы, необходимые при использовании каждой системы;

− математическую модель при подходе исследования операций или логическую модель при подходе анализа систем;

− критерий выбора предпочитаемой альтернативы.

1.2. Понятие системы, признаки системы и ее свойства

­ Слово «система» ­ древнегреческого происхождения. В античной философии им подчеркивалось, что мир не есть хаос, а обладает внутренним порядком, собственной организацией и целостностью. В современной науке существует достаточно много различающихся между собой определений и трактовок понятия система.

Система – ­ изложение науки в строгой последовательности; соединение нескольких предметов, действующих по одним и тем же законам [Словарь иностранных слов Михельсона, 1877].

Система – ­ совокупность взаимодействующих разных функциональ­ных единиц (биологических, человеческих, машинных, информацион­ных, естественных), связанная со средой и служащая достижению некоторой общей цели путем действия над материалами, энергией, биологическими явлениями и управления ими [В.И. Вернадский, 1926].

Система ­ – ­ множество объектов вместе с отношениями между ними и между их атрибутами [А. Холл, Р. Фейджин, 1975].

Система ­ – ­ ­ множество элементов, находящихся в отношениях и свя­зях друг с другом, образующих определенную целостность, единство [Советский энциклопедический словарь, 1979].

Приведенные определения являются типичными и отражают в том или ином виде аристотелевское утверждение, что целое есть нечто большее, чем сумма частей, и каждое из них обладает очевидной ограниченностью и неполнотой.

В теории системного анализа утверждается, что сущность такого предельно широкого и емкого понятия, как система, невозможно раскрыть через другие более частные сущности, и соответственно сформу­лировать его определение в виде одной сколь угодно сложной синтагмы. Вероятно, и стремиться к этому нет особой необходимости. С практической точки зрения его следует признать открытым, непрерывно разви­вающимся понятийным объектом, не определяемым исчерпывающим образом, в рамках каких бы то ни было логических или формальных построений. Нильс Бор по такому случаю писал: «Существуют первооб­разные понятия. Априори они не определены, но всякий раз нам необходимо удостовериться в том, что наши описания согласуются с их существованием» [Пригoжин, 1985].

Мы будем исходить из того, что при проведении системных анали­тических исследований сущность таких первообразных понятий может быть раскрыта только через выработанные практикой неформальные признаки, характеристики и классификации. Причем их не следует воспринимать как догму ­ в зависимости от целей и задач исследования они могут пополняться, уточняться и модифицироваться.

В настоящее время общепринято, что неформальными, содержа­тельными признаками системы являются: расчленимость, целостность, связанность и неаддитивность.

Расчленимость. Изучаемый объект расчленим, если существует возможность выде­лить в нем фиксированное число составных частей первого уровня, а в них ­ части второго уровня и так далее вплоть до последнего уровня, состоящего из неделимых далее частей. Составные части представленного таким образом объекта, кроме частей последнего уровня, называются подсистемами. Части последнего или низшего уровня принято имено­вать элементами (от лат. ­ elementum – первоначальное вещество). Эле­менты и подсистемы обозначаются обобщающим термином «компоненты»­ (от лат. ­ components – составляющий).

Целостность. Целостность исторически выступает родовым признаком системы. Формальное содержание этого признака заключается в следующем. Объект, состоящий из нескольких выделенных частей, обладает целост­ностью, если:

а) в нем в результате взаимодействия частей образуется новое каче­ство (общесистемное свойство), отсутствующее у частей;

б) каждая составная часть приобретает иные качества (системные свойства компонентов) по сравнению с качествами, присущими этим же частям вне данного объекта.

Связанность. Связанность рассматривается как признак, свидетельствующий о том, что целостные свойства изучаемого объекта и особые свойства его частей формируются за счет межкомпонентных (внутриуровневых и межуровневых) отношений, связей и взаимодействий. Уточним, что имеется в виду под понятиями «отношение», «связь» и «взаимодейст­вие». Отношение ­общенаучное понятие, используемое в системном анализе для соотнесения одного объекта с другим. Например, «часть ­– целое», «начальник ­– подчиненный», «управляющий –­ управляемый», «высший ­– низший».

Связь ­ общенаучное понятие, трактуемое в сис­темном анализе как коммуникационный канал или способ, с помощью которого реализуются взаимодействия между объектами. Взаимодействие (взаимное воздействие) ­ процесс перемещения вещества, энергии и информации между объектами, имеющий результат.

Неаддитивность. Неаддитивность (произв. от лат. additivus ­ получаемый путем сло­жения) как признак системы проявляется в том, что свойства изучаемого объекта невозможно свести к свойствам его частей, а также вывести лишь из них. Этот признак в несколько иной интерпретации можно выразить формулой: если изучаемый объект представляется в данном исследовании как система, то при любом способе разделения такого объекта на части невозможно выявить его целостные свойства.

К основным по­нятиям, характеризующим строение, функционирование и раз­витие систем, относятся:

элемент — это предел членения системы с точки зрения аспекта рассмотрения системы, решения конкретной задачи, по­ставленной цели (систему можно расчленять на элементы раз­личными способами в зависимости от формулировки задачи, це­ли и ее уточнения в процессе исследования);

компоненты и подсистемы — сложные системы принято вначале делить на подсистемы, а если последние сразу трудно делить на элементы, то составляющие промежуточных уровней называют компонентами системы;

связь — ограничение степени свободы элементов (элементы, вступая во взаимодействие друг с другом, утрачивают часть свойств, которыми потенциально обладали, находясь в свобод­ном состоянии);

цель - понятие цели и связанные с ним понятия целесооб­разности, целенаправленности лежат в основе развития си­стемы и направлены на улучшение системы.

Кроме этих основных понятий систему характеризуют несколько подчиненных понятий, описывающих ее поведение:

состояние - понятием состояние обычно характеризуют мгновенную фотографию, срез системы, остановку в ее развитии;

поведение - если система способна переходить из одного со­стояния в другое, то говорят, что она обладает поведением (этим понятием пользуются, когда неизвестны закономерности пере­хода из одного состояния в другое);

равновесие - понятие равновесие определяют, как способ­ность системы в отсутствии внешних возмущающих воздействий сохранять свое поведение как угодно долго;

устойчивость - это способность системы возвращаться в состояние равновесия после того, как она была из этого состоя­ния выведена под влиянием внешних возмущающих воздей­ствий.

Очень важную роль в моделировании систем играет поня­тие обратной связи, которая, может быть как положительной — сохраняющей тенденции происходящих в системе изменений то­го или иного параметра, так и отрицательной - противодей­ствующей тенденциям изменения входного параметра.

1.3. Классификация методов моделирования систем

Постановка любой задачи заключается в том, чтобы перевести её словесное, вербальное описание в формальное. В случае относительно простых задач такой переход осуществляется в сознании человека, который не всегда даже может объяснить, как он это сделал. Если полученная формальная модель (математическая зависимость между величинами в виде формулы, уравнения, системы уравнений) опирается на фундаментальный закон или подтверждается экспериментом, то этим доказывается её адекватность отображаемой ситуации, и модель рекомендуется для решения задач соответствующего класса.

По мере усложнения задач получение модели и доказательство её адекватности усложняется. Вначале эксперимент становится дорогим и опасным (например, при создании сложных технических комплексов, при реализации космических программ и т.д.), а применительно к экономическим объектам эксперимент становится практическим нереализуемым - задача переходит в класс проблем принятия решений. Постановка задачи и формирование модели, то есть перевод вербального описания в формальное, в этом случае становятся важными составными частями процесса принятия решения. Причём эти составные части не всегда можно выделить как отдельный этап, завершив который, можно обращаться с полученной формальной моделью так же, как с обычным математическим описанием, строгим и абсолютно справедливым. Большинство реальных ситуаций проектирования сложных технических комплексов и управления экономикой необходимо отображать классом самоорганизующихся систем, модели которых должны постоянно корректироваться и развиваться. При этом возможно изменение не только модели, но и метода моделирования, что часто является средством развития представления лица принимающего решение (ЛПР) о моделируемой ситуации.

Иными словами, перевод вербального описания в формальное, осмысление, интерпретация модели и получаемых результатов становятся неотъемлемой частью практически каждого этапа моделирования сложной развивающейся системы. Часто, для того чтобы точнее охарактеризовать такой подход к моделированию процессов принятия решений, говорят о создании как бы «механизма» моделирования, «механизма» принятия решений (например, «хозяйственный механизм», «механизм проектирования и развития предприятия» и т.п.).

Возникающие вопросы: как формировать такие развивающиеся модели или «механизмы», как доказывать адекватность моделей – и являются предметом системного анализа.

Для решения проблемы перевода вербального описания в формальное в различных областях деятельности стали развиваться специальные приёмы и методы. Так возникли методы типа «мозговой атаки», «сценариев», экспертных оценок, «дерева целей» и т.п.

В свою очередь, развитие математики шло по пути расширения средств постановки и решения трудно формализуемых задач. Наряду с детерминированными, аналитическими методами классической математики возникла теория вероятностей и математическая статистика (как средство доказательства адекватности модели на основе представительной выборки и понятия вероятности правомерности использования модели и результатов моделирования). Для задач с большей степенью неопределённости инженеры стали привлекать теорию множеств, математическую логику, математическую лингвистику, теорию графов, что во многом стимулировало развитие этих направлений. Иными словами, математика стала постепенно накапливать средства работы с неопределённостью, со смыслом, который классическая математика исключала из объектов своего рассмотрения.

Таким образом, между неформальным, образным мышлением человека и формальными моделями классической математики сложился «спектр» методов, которые помогают получать и уточнять (формализовать) вербальное описание проблемной ситуации, с одной стороны, и интерпретировать формальные модели, связывать их с реальной действительностью, с другой. Этот спектр условно представлен в таблице 2.

Таблица 2.

Вербальное описание	Формальная модель
Мозговая атака	Сценарий	Экспертные оценки	Дерево целей	…	Математическая логика	Теория множеств	Статистические методы	Аналитические методы

Развитие методов моделирования, разумеется, шло не так последовательно, как показано в табл. 2. Методы возникали и развивались параллельно. Существуют различные модификации сходных методов. Их по-разному объединяли в группы, т.е. исследователи предлагали разные классификации. Постоянно возникают новые методы моделирования как бы на «пересечении» уже сложившихся групп (рис. 1). Однако основную идею – существование «спектра» методов между вербальным и формальным представлением проблемной ситуации – эта таблица иллюстрирует.

Первоначально исследователи, развивающие теорию систем, предлагали классификации систем и старались поставить им в соответствие определённые методы моделирования, позволяющие наилучшим образом отразить особенности того или иного класса. Такой подход к выбору методов моделирования подобен подходу прикладной математики. Однако в отличие от последней, в основу которой положены классы прикладных задач, системный анализ может один и тот же объект или одну и ту же проблемную ситуацию (в зависимости от степени неопределённости и по мере познания) отображать разными классами систем и соответственно различными моделями, организуя, таким образом, как бы процесс постепенной формализации задачи, т.е. «выращивание» её формальной модели. Подход помогает понять, что неверно выбранный метод моделирования может привести к неверным результатам, к невозможности доказательства адекватности модели, к увеличению числа итераций и затягиванию решения проблемы.

Рис. 1 Методы моделирования систем.

1.4. Модели систем

Ввиду множественности различных систем существует более 35 их определений. Это объясняется тем, что определения есть языковая модель системы, и поэтому описание различных видов систем (искусственная, естественная) определяется по-разному, т.е. приводят к различным определениям. Кроме того, поскольку один и тот же объект (система) выполняет разные цели, это также создаёт множество определений.

Наиболее простое определение системы – это средство достижения цели, а цель – это субъективный абстрактный образ ещё не существующего, но желаемого состояния среды или окружающего нас мира.

Сформулировать цель даже существующих систем сложно, тем более сформулировать цель проектирования систем. Поэтому для облегчения решения задачи создания систем необходимо применение моделирования, так как для определений и точной характеристики любой системы следует совершенствовать и развивать её модель.

Наиболее простой моделью системы является модель «чёрного ящика» (рис. 2). Идея использования «чёрного ящика» возникла от недостаточности информации о внутреннем строении (составе) самой системы, поэтому её мы изображаем в виде непрозрачного чёрного ящика, который обладает следующими свойствами: целостность его и обособленность от среды.

Первое свойство говорит о том, что ящик обособлен, т.е. выделен из среды, но не является полностью изолированным от нас. Ящик (система) связан со средой связями. Как среда действует на него, так и он действует на среду.

Наряду с очевидной простотой модели «чёрного ящика» она (простота) обманчива. При описании любой реальной системы очень часто мы сталкиваемся с трудностями в определении всех входов и выходов этой системы. Использование модели «чёрного ящика» даёт те результаты, которые определяются целью системы. Выбор входов «чёрного ящика» является противоположной задачей.

Не учёт некоторых входных или выходных параметров системы приводит часто к плохому достижению поставленной цели.

Рис.2 Схема модели «черного ящика».

Данная модель описывает основные составные части системы. На первый взгляд, эта модель, кажется простой. Но если дать задание экспертам определить состав одной и той же системы, то у каждого эксперта будет своя модель, отличающаяся от моделей других. Это объясняется тем, что, во-первых, понятие элемента у всех будет разным. Во-вторых, поскольку модель состава является деловой, то для различных целей требуются различные составные части этой системы. И, в-третьих, деление всей системы на подсистемы является относительным или условным, так как границы этих подсистем, число этих подсистем и их состав будут различными, а значит и модели будут разными.

При использовании системного подхода особого внимания заслуживают четыре очень важные проблемы:

1) определение границ системы в целом, границ окружающей среды, или окружения;

2) установление целей системы;

3) определение структуры программы и построение матрицы «программы – элементы»;

4) описание управления системой

Центральной проблемой системного анализа является проблема принятия решения. Применительно к задачам исследования, проектирования и управления сложными системами проблема принятия решения связана с выбором определённой альтернативы в условиях различного рода неопределённости. Неопределённость обусловлена многокритериальностью задач оптимизации, неопределённостью целей развития систем, неоднозначностью сценариев развития системы, недостаточностью априорной информации о системе, воздействием случайных факторов в ходе динамического развития системы и прочими условиями. Учитывая данные обстоятельства, системный анализ можно определить как дисциплину, занимающуюся проблемами принятия решений в условиях, когда выбор альтернативы требует анализа сложной информации различной физической природы.

Главным содержанием дисциплины «Системный анализ» являются сложные проблемы принятия решений, при изучении которых неформальные процедуры представления здравого смысла и способы описания ситуаций играют не меньшую роль, чем формальный математический аппарат.

Системный анализ является дисциплиной синтетической. В нём можно выделить три главных направления. Эти три направления соответствуют трём этапам, которые всегда присутствуют в исследовании сложных систем:

1) построение модели исследуемого объекта;

2) постановка задачи исследования;

3) решение задачи принятия решений.

Рассмотрим данные этапы.

1.4.1. Построение модели

Для традиционных наук начальный этап работы заключается в постановке формальной задачи, которую надо решать. В исследовании сложной системы это промежуточный результат, которому предшествует длительная работа по структурированию исходной проблемы. Начальный пункт в системном анализе связан с формулированием проблемы. Здесь следует отметить следующую особенность задач системного анализа. Необходимость системного анализа возникает тогда, когда заказчик уже сформулировал свою проблему, т.е. проблема не только существует, но и требует решения. Однако системный аналитик должен отдавать себе отчёт в том, что сформулированная заказчиком проблема представляет собой приблизительный рабочий вариант. Причины, по которым исходную формулировку проблемы необходимо считать в качестве первого приближения, состоят в следующем. Система, для которой формулируется цель проведения системного анализа, не является изолированной. Она связана с другими системами, входит как часть в состав некоторой надсистемы. Поэтому, формулируя проблему для рассматриваемой системы, необходимо учитывать, как решение данной проблемы отразится на системах, с которыми связана данная система. Неизбежно планируемые изменения затронут и подсистемы, входящие в состав данной системы, и надсистему, содержащую данную систему. Таким образом, к любой реальной проблеме следует относиться не как к отдельно взятой, а как к объекту из числа взаимосвязанных проблем.

При формулировании проблемы системный аналитик должен следовать некоторым рекомендациям.

Во-первых, за основу должно браться мнение заказчика. Как правило, в качестве такового выступает руководитель организации, для которой проводится системный анализ. Именно он, как было отмечено выше, генерирует исходную формулировку проблемы. Далее системный аналитик, ознакомившись со сформулированной проблемой, должен уяснить задачи, которые были поставлены перед руководителем, ограничения и обстоятельства, влияющие на поведение руководителя, противоречивые цели, между которыми он старается найти компромисс. Системный аналитик должен изучить организацию, для которой проводится системный анализ. Необходимо тщательно ознакомиться с существующей иерархией управления, функциями различных групп, а также предыдущими исследованиями соответствующих вопросов, если таковые проводились. Аналитик должен воздерживаться от высказывания своего предвзятого мнения о проблеме и от попыток втиснуть её в рамки своих прежних представлений ради того, чтобы использовать желательный для себя подход к её решению. Наконец, аналитик не должен оставлять непроверенными утверждения и замечания руководителя. Как уже отмечалось, проблему, сформулированную руководителем, необходимо, во-первых, расширять до комплекса проблем, согласованных с над- и подсистемами, и, во-вторых, согласовывать её со всеми заинтересованными лицами.

Следует также отметить, что каждая из заинтересованных сторон имеет своё видение проблемы, отношение к ней. Поэтому при формулировании комплекса проблем необходимо учитывать, какие изменения и почему хочет внести та или другая сторона. Кроме того, проблему необходимо рассматривать всесторонне, в том числе и во временном, историческом плане. Требуется предвидеть, как сформулированные проблемы могут измениться с течением времени или в связи с тем, что исследование заинтересует руководителей другого уровня. Формулируя комплекс проблем, системный аналитик должен знать развёрнутую картину того, кто заинтересован в том или ином решении.

Краеугольным камнем системного анализа является математическое моделирование. Хотя данные, полученные в процессе исследования математических моделей, являются основой для принятия решений, окончательный выбор обычно делается с учетом многих других "нематериальных" (не имеющих числового выражения) факторов (таких как человеческое поведение), которые невозможно отобразить в математических моделях. Построение модели (формализация изучаемой системы, процесса или явления) есть описание процесса на языке математики. При построении модели осуществляется математическое описание явлений и процессов, происходящих в системе. Поскольку знание всегда относительно, описание на любом языке отражает лишь некоторые стороны происходящих процессов и никогда не является абсолютно полным. С другой стороны, следует отметить, что при построении модели необходимо уделять основное внимание тем сторонам изучаемого процесса, которые интересуют исследователя. Глубоко ошибочным является желание при построении модели системы отразить все стороны существования системы. При проведении системного анализа, как правило, интересуются динамическим поведением системы, причём при описании динамики с точки зрения проводимого исследования есть первостепенные параметры и взаимодействия, а есть несущественные в данном исследовании параметры. Таким образом, качество модели определяется соответствием выполненного описания тем требованиям, которые предъявляются к исследованию, соответствием выполненного описания тем требованиям, которые предъявляются к исследованию, соответствием получаемых с помощью модели результатов ходу наблюдаемого процесса или явления. Построение математической модели есть основа всего системного анализа, центральный этап исследования или проектирования любой системы. От качества модели зависит результат всего системного анализа.

Любые методы системного анализа опираются на математическое описание изучаемого объекта (процесса). В настоящее время выработан ряд общих принципов и подходов, используемых при моделировании.

1.4.2. Постановка задачи исследования

После того как сформулирована проблема, которую требуется преодолеть в ходе выполнения системного анализа, переходят к определению цели. Цель исследования предполагается внешним фактором по отношению к системе. Таким образом, цель становится самостоятельным объектом исследования. Цель должна быть формализована. Задача системного анализа состоит в проведении необходимого анализа неопределённостей, ограничений и формулировании, в конечном счёте, некоторой оптимизационной задачи. Таким образом, задача системного анализа на этом этапе трактуется как некоторая оптимизационная проблема.

Формулируя цель, требуется всегда отдавать отчёт в том, что она играет активную роль в управлении. В определении цели было отражено, что цель – это желаемый результат развития системы. Таким образом, сформулированная цель системного анализа будет определять весь дальнейший комплекс работ. Следовательно, цели должны быть реалистичны. Задание реалистичных целей направит всю деятельность по выполнению системного анализа на получение определённого полезного результата. Важно также отметить, что представление о цели зависит от стадии познания объекта, и по мере развития представлений о нём цель может быть переформулирована. Изменение целей во времени может происходить не только по форме,

в силу всё лучшего понимания сути явлений, происходящих в исследуемой системе, но и по содержанию, вследствие изменения объективных условий и субъективных установок, влияющих на выбор целей. Сроки изменения представлений о целях, старения целей различны и зависят от уровня иерархии рассмотрения объекта. Цели более высоких уровней долговечнее. Динамичность целей должна учитываться в системном анализе.

При формулировании цели нужно учитывать, что на цель оказывают влияние как внешние по отношению к системе факторы, так и внутренние. При этом внутренние факторы являются такими же объективно влияющими на процесс формирования цели факторами, как и внешние. Далее следует отметить, что даже на самом верхнем уровне иерархии системы имеет место множественность целей. Анализируя проблему, необходимо учитывать цели всех заинтересованных сторон. Среди множества целей желательно попытаться найти или сформировать глобальную цель. Если этого сделать не удаётся, следует ранжировать цели в порядке их предпочтения для снятия проблемы в анализируемой системе. Исследование целей заинтересованных в проблеме лиц должно предусматривать возможность их уточнения, расширения или даже замены. Это обстоятельство является основной причиной итеративности системного анализа. На выбор целей субъекта решающее влияние оказывает та система ценностей, которой он придерживается, поэтому при формировании целей необходимым этапом работ является выявление системы ценностей, которой придерживается лицо, принимающее решение.

Анализируя требования к системе, т.е. цели, которые предполагает достигнуть исследователь, и те неопределённости, которые при этом неизбежно присутствуют, исследователь должен сформулировать цель анализа на языке математики. Язык оптимизации оказывается здесь естественным и удобным, но вовсе не единственно возможным.

При решении задачи принятия решения исследуется система, которая условно изображается прямоугольником, рис. 2. Определение системы уже было дано. В дальнейшем под системой будем понимать совокупность объектов, характеризующихся некоторыми показателями. Все эти показатели или параметры подразделяются, прежде всего, на входные и выходные. Выходные показатели графически обозначаются стрелками, выходящими из прямоугольника – системы; к ним относятся такие показатели, как, например, качество продукта, себестоимость, производительность, количество и др. Параметры, которые можно изменить в соответствии с нашим желанием, обозначаются и называются входными воздействиями. Такими параметрами могут быть количество финансовых средств, которые вкладываются в то или иное производство, оборудование, поставляемое в тот или иной цех, людские ресурсы и т.п. Входные параметры являются "рулями", которыми управляют, изменяя их значение, соответственно изменяются и выходные параметры .

Выбор тех или иных величин и является решением задачи принятия решений. Если принято решение, следовательно, определены значения выходных параметров , и в этом случае говорят, что система перешла в некоторое новое состояние. Оператор, отражающий зависимость выходных параметров от входных управляющих параметров , называется моделью

.

(6.1)

Здесь 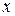– элемент некоторого нормированного пространства , определяемого природой модели, , где – множество, которое может иметь сколь угодно сложную природу, определяемую структурой модели и особенностями исследуемой системы.

Математическая модель представляет собой математическую зависимость, позволяющую без экспериментов, зная управляющие воздействия, определить выходные параметры. Использование моделей очень удобно, так как не всегда можно провести эксперименты, при их проведении можно даже разорить предприятие, однако, имея модель, можно проиграть различные ситуации на ней. После того как принято решение, хорошее или плохое, его необходимо охарактеризовать численно. Для этого вводится целевая функция, позволяющая численно оценить насколько принятое решение хорошо. Эта функция зависит от входных и выходных параметров и обозначается 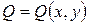. Так как выходные параметры можно выразить через входные , что часто и делают, то тогда целевая функция будет зависеть только от управляющих показателей – . И задача заключается в нахождении таких управлений (или таких решений ), при которых целевая функция достигала бы своего минимального (максимального) значения.

Например, целевой функцией является прибыль – требуется, чтобы она была максимальной, если целевая функция представляет собой себестоимость, то необходимо, чтобы она была минимальной. В конкретных задачах часто накладываются ограничения, например, требуют, чтобы при нахождении максимума целевой функции себестоимость была бы не выше заданной, количество товара по каждой номенклатуре также было бы не меньше заданного и т.д.

Таким образом, задача состоит в том, чтобы найти такое решение, при котором целевая функция принимает максимальное (минимальное) значение и удовлетворяются все ограничения экономического, технологического планов, которые принято записывать в виде

.

(6.2)

Изменяя управляющую переменную , вычисляют по модели (6.1) значения выходной переменной , а затем целевой функции . После этого среди всех принятых решений ищется такое решение , при котором значение будет наилучшим. Варьировать значениями управляющей переменной можно только в определенных пределах. Например, денежный вклад должен быть, с одной стороны, больше нуля, а, с другой стороны, меньше некоторого предельного значения, определяемого финансовыми возможностями конкретного лица, т.е. или, если – область допустимых значений варьируемых управлений , то .

Математически данная задача записывается следующим образом: требуется принять такое решение , принадлежащее области допустимых решений, , при котором целевая функция достигает своего минимального значения

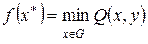
и выполняются связи, определяемые математической моделью (6.1), а также ограничения в виде неравенств (6.2), которыми задаются технологические ограничения.

Управляющие переменные, удовлетворяющие требованиям и ограничениям (6.2), называются допустимым решением. Все остальные решения недопустимы. Допустимые решения , при котором целевая функция минимальна, называется оптимальным решением.

Основной задачей теории принятия решения является нахождение оптимального решения. Для этого необходимо: построить модель (6.1), определить целевую функцию 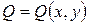, определить область допустимых управлений , определить технологические ограничения (6.2).

На практике встречаются задачи нахождения не оптимального, а допустимого решения, т.е. решения, удовлетворяющего системе ограничений. В этом случае задача ставится следующим образом: найти такие , при которых выполнены ограничения (6.2). Такие задачи могут иметь не единственное решение.

Некоторые задачи теории принятия решения пассивны, для них характерно, что входные управляющие параметры не влияют на целевую функцию. В таких задачах только проверяют, допустима полученная система или нет, и решением является "да" или "нет". Если известна модель , то проверяется условие , и задача заключается в том, чтобы по построенной модели проверить при всех ли показатели 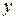хорошие, и на основании этого сделать вывод о пригодности системы или ее непригодности.

Для решения всех перечисленных задач применяют различные методы, которые и рассмотрим далее.

1.4.3. Решение задачи принятия решений

Только этот третий этап анализа можно отнести собственно к этапу, использующему в полной степени математические методы. Хотя без знания математики и возможностей её аппарата успешное выполнение двух первых этапов невозможно, так как и при построении модели системы, и при формулировании цели и задач анализа широкое применение должны находить методы формализации. Однако отметим, что именно на завершающем этапе системного анализа могут потребоваться тонкие математические методы. Но следует иметь в виду, что задачи системного анализа могут иметь ряд особенностей, которые приводят к необходимости применения наряду с формальными процедурами эвристических подходов. Причины, по которым обращаются к эвристическим методам, в первую очередь связаны с недостатком априорной информации о процессах, происходящих в анализируемой системе. Также к таковым причинам можно отнести большую размерность вектора 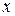и сложность структуры множества . В данном случае трудности, возникающие в результате необходимости применения неформальных процедур анализа, зачастую являются определяющими. Успешное решение задач системного анализа требует использования на каждом этапе исследования неформальных рассуждений. Ввиду этого проверка качества решения, его соответствие исходной цели исследования превращается в важнейшую теоретическую проблему.