В этом случае система ограничений задачи имеет вид

(2.30)

Пусть по методу наискорейшего спуска мы построили точки и убедились (подставляя в (2.30) координаты этих точек), что лежат в области решений, а точка уже не лежит в ней.

Значит координаты точки не удовлетворяют хотя бы одному неравенству системы (2.30), например неравенству (здесь i - номер конкретного неравенства).

Пусть 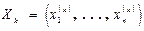, и , т.е.

. (2.31)

Здесь - направление спуска, которое совпадает с направлением при отыскании максимума или с направлением - при отыскании минимума.

Чтобы остаться в пределах области решений, следует вместо точки взять точку, лежащую на том же направлении спуска, т.е. с координатами, удовлетворя-ющими условию (2.11), но с меньшей длиной шага .

Значение нужно выбирать так, чтобы точка оказалась на границе области решений, т.е. чтобы выполнялось равенство.

Учитывая (2.31), получаем и

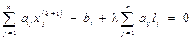
Отсюда (2.32)

Формула (2.32) дает значение , при котором направление спуска пересекает границу области решений.

Если координаты точки не удовлетворяют нескольким неравенствам системы (2.30), то нужно найти по формуле (2.32) для каждого из этих неравенств и взять наименьшее из найденных значений.

Подставляя его в (2.31), найдем координаты точки , которая будет исходной для следующего шага решения.

Так как проекция градиента задачи с линейными ограничениями лежит на границе области решений, а для случая двух переменных - просто на прямой , то направление спуска l на следующем шаге берется на этой границе.

Оптимум достигается в той точке, в которой градиент перпендикулярен границе области решений.

Замечание. Если прямая на плоскости имеет уравнение Ax+By+C=0,

то ее направление задается вектором l’=(B;-A) или вектором l’’=(-B; A).

Итак, процесс нахождения решения задачи выпуклого программирования методом наискорейшего спуска включает следующие этапы:

1. Выбираем любую точку , удовлетворяющую области решений.

2. Находим частные производные, а затем градиент функции в точке.

3. Определяем шаг l.

4. По формулам 2.27 и 2.28 находим точку .

5. Проверяем, находится ли точка внутри области решений.

6. Проверяем точку на оптимальность. Если эта точка не является оптимальным решением, то повторяем пункты 2 — 6.

Пример 1. Используя метод скорейшего спуска, найти максимум функции при ограничениях:

Решение. Отметим, что функция Z вогнутая, т.е. данная задача является задачей выпуклого программирования.

Находим частные производные функции Z и

записываем общее выражение ее градиента:

.

1) В качестве исходной возьмем точку (ее координаты удовлетворяют системе ограничений).

Далее, используя формулы (2.7) и (2.8) находим точку : .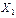

Тогда

.

Отсюда , т.е.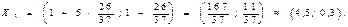

Так как 4,5+0,6<10 и 4,5+0,3<6, то находится внутри области решений.

2) Находим

Можно не производить этих вычислений. Достаточно убедиться, что первая компонента положительна, и тогда взять . (В самом деле, , так как , то и имеет тоже направление, что и ).

Теперь

,

откуда, т.е. и .

Мы видим, что лежит уже вне области решений, причем не выполняются первое и второе неравенства.

По формуле (2.12) находим 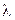для обоих неравенств:

,

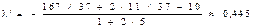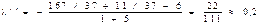
Берем и теперь получаем .

Нетрудно убедиться, что эта точка лежит на границе области

3) Попав на границу области, мы должны двигаться по ней в сторону увеличения функции Z.

В виду замечания, сделанного после рассмотрения метода наискорейшего спуска, направление прямой задается вектором l’ = или l’’ =(-1;1).

По формуле (1.5) находим производную функции Z по направлению l’ в точке :

Значит, в этом направлении функция Z убывает и в качестве направления спуска следует взять l’’ =(-1;1).

Итак,

Далее поступаем, как и на предыдущих шагах:

.

Отсюда и

Так как (4,6+2,8)<10, то точка является решением данной задачи.

Поскольку,

проекция градиента на это направление равна 0, значит, мы достигли оптимального значения функции при данных ограничениях.

Таким образом, X* =(4,6; 1,4) и

.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ

Динамическое программирование (динамическое планирование) - оптимально планировать управляемые процессы (на ход которых мы можем в той или иной степени влиять), в которых процесс принятия решений можно разбить на этапы (шаги).

Такие операции называют многошаговыми.