Метод множителей Лагранжа

Пусть задана задача математического программирования: максимизировать функцию

Z=f(x₁, x₂,..., x_n) (2.7)

при ограничениях

g_i(x₁, x₂,..., x_n)=0, i =1,..., m.

Ограничения в задаче заданы уравнениями, поэтому для ее решения можно воспользоваться классическим методом отыскания условного экстремума функций нескольких переменных.

При этом полагаем, что функции f(x₁, x₂,..., x_n) и

g_i(x₁, x₂,..., x_n)=0 (i =1,..., m) непрерывны вместе со своими первыми частными производными.

Для решения задачи составим функцию

F(x₁,x₂,...,x_n, l₁,l₂,...,l_m) = f(x₁,x₂,...,x_n) + , (2.8)

определим частные производные

и приравняем их нулю.

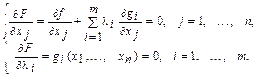В результате получим систему уравнений

(2.9)

Функция (2.8) называется функцией Лагранжа, а числа l_i — множителями Лагранжа.

Если функция Z=f(x₁,x₂,...,x_n) в точке X⁽⁰⁾=() имеет экстремум, то существует такой вектор , что точка является решением системы (2.9).

Следовательно, решая систему (2.9), получаем множество точек, в которых функция Z может иметь экстремальные значения.

При этом неизвестен способ определения точек глобального минимума или максимума.

Однако если решения системы найдены, то для определения глобального максимума (минимума) достаточно найти значения функции в соответствующих точках.

Если для функций Z=f(x₁,x₂,...,x_n) и g_i(x₁,x₂,...,x_n) (i =1... m) существуют вторые частные производные и они непрерывны, то можно вывести достаточное условие существования локального экстремума функции в точке, являющейся решением системы (2.9).

Однако практическое значение этого условия невелико.

Метод множителей Лагранжа имеет ограниченное применение, т.к. система (2.9), как правило, имеет несколько решений.

Нелинейное программирование как новая математическая дисциплина возникла главным образом в связи с указанной ограниченностью метода множителей Лагранжа.

Таким образом, определение экстремальных точек задачи (2.8) методом множителей Лагранжа включает следующие этапы:

1. Составление функции Лагранжа.

2. Нахождение частных производных от функции Лагранжа по переменным x_j и l_i и приравнивание их к нулю.

3. Решая систему уравнений (2.9), находят точки, в которых целевая функция задачи может иметь экстремум.

4. Среди точек, подозрительных на экстремум, находят такие, в которых достигается экстремум, и вычисляют значение функции (2.7) в этих точках.

П р и м е р 1. Найти точку условного экстремума

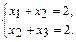функции Z=x₁x₂+x₂x₃ при ограничениях

Р е ш е н и е. Составим функцию Лагранжа

F(x₁,x₂,x₃,l₁,l₂) = x₁x₂+x₂x₃ + l₁(x₁+x_2-- 2 ) + l₂(x₂+x₂- 2 ) и продифференцируем ее по переменным x₁, x₂, x₃, l₁ и l₂.

Приравнивая полученные выражения к нулю, получаем

следующую систему уравнений:

Из первого и третьего уравнения следует, l₁ = l₂ = -x_2; тогда

Решая данную систему, находим: x₁ = x₂ = x₃ =1, Z =2.