 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Метод потенциалов
|
|
Транспортная задача заключается в определении оптимального плана перевозок однородного груза из m пунктов отправления А1,А2...,Аm в n пунктов потребления и где критерием оптимальности является стоимость пере-возок всех грузов, которая должна быть минимальной.
Экономико-математическая модель транспортной задачи
содержит системы линейных уравнений
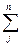 xij=ai, i =
xij=ai, i =  ; (1)
; (1)
 xij=bj, j =
xij=bj, j = 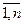 , (2)
, (2)
условие неотрицательности переменных Ху
xij ³ 0, i =  ; j =
; j = 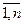 (3)
(3)
и целевую функцию
F(X) = 
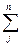 cij · xij ® max (4)
cij · xij ® max (4)
Следует иметь в виду, что:
1. Всякое неотрицательное решение системы линейных уравнений, определяемое матрицей Х=(хij), i =  ; j =
; j = 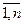 называется допустимым планом транспортной задачи.
называется допустимым планом транспортной задачи.
2. Ранг матрицы, составленный из коэффициентов при неизвестных системы линейных уравнений транспортной задачи, на единицу меньше числа уравнений, т.е. равен (m + n - 1).
Следовательно, число линейно независимых уравнений равно (m + n - 1), они образуют базис, а соответ-ствующие им (m + n - 1) переменных будут являться базисными.
3. Допустимый план транспортной задачи, имеющий не более (m + n - 1 ) отличных от нуля величин xij, назы-вается опорным.
4. Если в опорном плане число отличных от нуля компонент равно в точности (m + n - 1 ), то план является невырожденным, если меньше, то план называется вырожденным.
5. План X '= (хij) i =  ; j =
; j = 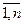 , при котором функция (4) принимает свое минимальное значение, называется оптимальным планом транспортной задачи.
, при котором функция (4) принимает свое минимальное значение, называется оптимальным планом транспортной задачи.
6. Для решения транспортной задачи необходимо и доста-точно, чтобы суммарные запасы груза в пунктах отправ-ления были равны сумме заявок пунктов назначения:
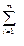 ai =
ai =  bj (5)
bj (5)
7. Модель транспортной задачи, удовлетворяющая условию (5), называется закрытой.
Если же указанное условие не выполняется, то модель называется открытой.
В случае превышения запаса над заявками
 ai >
ai >  bj
bj
вводится фиктивный (n+1) пункт назначения с
потребностью
bm+1 =  ai -
ai - 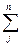 bj
bj
и соответствующие тарифы считаются равными нулю:
ci,n +1 = 0, i = 
При  ai <
ai <  bj вводится фиктивный (m + 1 ) пункт отправления с запасом груза am+ 1 =
bj вводится фиктивный (m + 1 ) пункт отправления с запасом груза am+ 1 =  bj —
bj —  ai и соответствующие тарифы принимаются равными нулю: cm +1, j = 0, j=
ai и соответствующие тарифы принимаются равными нулю: cm +1, j = 0, j= 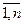 ,.
,.
8. Наилучшим элементом матрицы тарифов С называется:
— наименьший тариф, если задача поставлена на минимум,
— наибольший тариф, если задача поставлена на максимум целевой функции.
Рассмотрим один из методов построения первого опорного плана - метод наименьших тарифов (стоимости).
Алгоритм построения первого опорного плана методом наименьшей стоимости включает следующие этапы:
I среди тарифов находится наименьший;
II клетка с выбранным тарифом заполняется величиной, равной максимально возможному объему груза с учетом ограничений по строке и столбцу.
При этом либо весь груз вывозится от соответствующего поставщика, либо полностью удовлетворяется заявка потребителя.
Строка или столбец таблицы вычеркивается и в дальнейшем распределении не участвует;
III из оставшихся тарифов вновь находится наилучший (наименьший), и процесс продолжается до тех пор, пока не будет распределен весь груз.
Если модель транспортной задачи открытая и введены фиктивный поставщик или потребитель, то —
² распределение осуществляется сначала для действительных поставщиков и потребителей,
² и в последнюю очередь нераспределенный груз направляется от фиктивного поставщика или к фиктивному потребителю.
9. Дальнейшее улучшение первого опорного плана и получение оптимального плана производим методом потенциалов, который основан на теории двойственности.
План Х = (хij) транспортной задачи будет являться оптимальным, если существует система т + п чисел αi и βj, называемых потенциалами, удовлетворяющая условиям:
I. F( ) -> min
) -> min
αi + βj = cij для занятых клеток, где хij > О (6)
αi + βj ≤ cij для не занятых клеток, где хij = О
II. F( ) -> max
) -> max
αi + βj = cij для занятых клеток, где хij > О (7)
αi + βj ≥ cij для не занятых клеток, где хij = О
Потенциалы αi и βj являются переменными двойственной транспортной задачи и обозначают оплату за перевозку единицы груза в пунктах отправления (поставщиками) и назначения (потребителями) соответственно.
Поэтому их сумма равна транспортному тарифу αi + βj = cij, а условия (6),(7) получены на основании второй теоремы двойственности.
Введем обозначение оценки свободной клетки таблицы
Δ ij = αi + βj — cij
Если среди оценок Δ ij нет положительных (задача поставлена на минимум), то опорный план является оптимальным.
Алгоритм оценки оптимальности плана методом потенциалов включает следующие этапы.
I. Построение первого опорного плана.
II. Проверка вырожденности плана.
Потенциалы αi и βj могут быть рассчитаны только для невырожденного плана.
Если число занятых клеток в опорном плане меньше, чем (m + n - 1 ), то не хватит количества уравнений для определения потенциалов.
Поэтому вносим нуль в одну из свободных клеток таблицы так, чтобы общее число занятых клеток стало равным (m + n — 1 ).
Нуль вводят в клетку с наименьшим тарифом, например в клетку одновременно вычеркиваемых строки и столбца таблицы при составлении нового плана.
При этом фиктивно занятая нулем клетка не должна образовывать замкнутого прямоугольного контура с другими клетками таблицы.
III. Определение значения функции цели путем суммирования произведений тарифов (удельных затрат) на объем перевозимого груза по всем занятым клетками таблицы.
IV. Проверка условия оптимальности.
Определяем потенциалы αi и βj.
Для каждой занятой клетки таблицы записываем уравнение αi + βj = cij (i =  ; j =
; j = 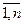 ).
).
Получим систему (m + п - 1 ) уравнений с (m + п) переменными.
Так как число переменных больше числа уравнений (m + п > m + п — 1 ), то система является неопределенной и имеет бесконечное множество решений.
Поэтому одному из неизвестных потенциалов αi, βj, задают произвольное значение, например, для простоты вычислений полагаем α 1 = 0.
Тогда остальные потенциалы определяются из приведенных соотношений.
В транспортную таблицу добавляются дополнительная строка и столбец, куда заносятся потенциалы.
Определяем оценки свободных клеток Δ ij.
Если все Δ ij ≤ 0 (задача решается на минимум целевой функции), либо все Δ ij ≥ 0 (задача решается на максимум), то оптимальный план найден.
Если хотя бы одна оценка свободной клетки Δ ij > 0 (задача поставлена на минимум) или Δ ij < О (задача поставлена на максимум), план не является оптимальным, его можно улучшить, осуществив перераспределение груза.
V. Построение нового опорного плана.
Из всех положительных оценок свободных клеток выбираем наибольшую (если задача поставлена на минимум).
Из всех отрицательных — наибольшую по абсолютной величине (если задача поставлена на максимум).
Клетку, которой соответствует наибольшая оценка, следует заполнить, т.е. направить груз.
Заполняя выбранную клетку, необходимо изменить объемы поставок, записанных в ряде других занятых и связанных с заполняемой так называемым циклом.
 Циклом, или прямоугольным контуром, в таблице условий транспортной задачи называется ломаная линия, вершины которой расположены в занятых клетках таблицы, а звенья - вдоль строк и столбцов, причем в каждой вершине цикла встречаются ровно два звена, одно из которых находится в строке, другое — в столбце.
Циклом, или прямоугольным контуром, в таблице условий транспортной задачи называется ломаная линия, вершины которой расположены в занятых клетках таблицы, а звенья - вдоль строк и столбцов, причем в каждой вершине цикла встречаются ровно два звена, одно из которых находится в строке, другое — в столбце.
Если ломаная линия, образующая цикл, пересекается, то точки пересечения не являются вершинами.
Для каждой свободной клетки таблицы можно построить единственный цикл.
Вершинам цикла, начиная от вершины, находящейся в свободной клетке, присваиваем поочередно знаки «+» и «—».
Из объемов груза, стоящих в минусовых клетках, выбираем наименьшее и обозначим его γ.
Перераспределяем величину γ по циклу, прибавляя γ к соответствующим объемам груза, стоящим в плюсовых клетках и вычитая γ из объемов груза, находящихся в минусовых клетках таблицы.
В результате клетка, которая ранее была свободной, становится занятой, а одна из занятых клеток цикла становится свободной.
Полученный новый опорный план проверяется на оптимальность, т.е. возвращаемся к четвертому этапу алгоритма.
Примечания:
1. Если в минусовых клетках построенного цикла находятся два (или несколько) одинаковых минимальных значения xij, то при перераспределении объемов груза освобождаются две (или несколько) клеток, и план становится вырожденным.
Для продолжения решения необходимо одну или несколько освобождающихся клеток таблицы занять нулем, причем предпочтение отдается клетке с наилучшим тарифом.
Нулей вводится столько, чтобы во вновь полученном опорном плане число занятых клеток было равно (m + n — 1 ).
2. Если в оптимальном плане транспортной задачи оценка свободной клетки равна нулю (Δ ij = 0), то задача имеет множество оптимальных планов.
Для клетки с нулевой оценкой можно построить цикл и перераспределить груз.
В результате полученный оптимальный план будет иметь такое же значение целевой функции.
3. Значение целевой функции на каждой итерации можно рассчитать следующим образом:
F( k )=F(
k )=F( k - 1 )—γΔ ij (задача поставлена на минимум);
k - 1 )—γΔ ij (задача поставлена на минимум);
F( k )=F(
k )=F( k - 1 ) + γΔ ij (задача поставлена на максимум),
k - 1 ) + γΔ ij (задача поставлена на максимум),
где γ - величина перемещаемого по циклу объема груза;
Δ ij - оценка свободной клетки, в которую направляется груз при переходе к новому плану;
F( k ) — значение целевой функции на k -й итерации;
k ) — значение целевой функции на k -й итерации;
F( k - 1 ) —значение целевой функции на предыдущей итерации.
k - 1 ) —значение целевой функции на предыдущей итерации.
Пример 1. На три базы A1, A2, А3, поступил однородный груз в количествах, соответственно равных 6, 8, 10 ед.
Этот груз требуется перевезти в четыре магазина B1, В2, B3, В4 соответственно в количествах 4, 6, 8, 8 ед.
Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов (тыс.руб. за ед. груза):
 1 2 4 3
1 2 4 3
Cij = 4 3 8 5 i = 1,2,3; j= 1,2,3,4.
2 7 6 3
Надо составить план перевозок однородного груза с минимальными транспортными издержками.
Проверим необходимое и достаточное условие разрешимости задачи.
 aij = 6 + 8 + 10 = 24,
aij = 6 + 8 + 10 = 24,
 = 4 + 6 + 8 + 8 = 26.
= 4 + 6 + 8 + 8 = 26.
Как видно, суммарная потребность груза в пунктах назначения превышает запасы груза на трех базах.
Следовательно, модель исходной транспортной задачи является открытой.
Чтобы получить закрытую модель, введем дополнительную (фиктивную) базу с запасом груза, равным 2 ед. (26-24).
Тарифы перевозки единицы груза из базы A 4, во все магазины полагаем равными нулю.
Занесем исходные данные в распределительную табл. 7.1.
| Bj Ai | В 1 | B2 | B3 | B4 | Запасы аi | |
| βj αi | β 1=1 | β 2=2 | β 3=7 | β 4=4 | ||
| A 1 | α 1=О |

|
 — —
  2 2
|  4 4

| ||
| A 2 | α 2=1 |  3 3
 + +
| — | |||
| A 3 | α 3=-1 |
 2 2
| ||||
| A 4 | α 4=-7 | |||||
| Потребности bj | Σ=26 Σ=26 |
1. Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.
Среди тарифов из всей таблицы наименьшим является С 11 = 1, поэтому в клетку A 1 B 1 направляем максимально возможный груз. Он равен min{6,4} = 4.
Тогда х 11 = 4 и из базы A 1 не вывезен груз в размере 2 ед., а потребность магазина В 1 удовлетворена полностью.
Столбец таблицы B 1 выходит из рассмотрения.
Из оставшихся тарифов строки наименьший – с 12 = 2.
В клетку A1B2 направляем максимально возможный груз, равный min{2,6} = 2.
Тогда строка A1 выходит из рассмотрения, поскольку из базы A1 вывезен весь груз, а потребность второго магазина не удовлетворена на 4 единицы.
Из оставшихся тарифов наилучший с 22 = 3 и c34 = 3.
В клетку A2B2 направляем груз, равный min{8,4} = 4.
При этом вычеркивается столбец В 2 из рассмотрения.
Из оставшихся тарифов наименьший с 34 = 3.
В клетку A3B1 направляем груз, равный min{10,8} = 8.
При этом потребность четвертого магазина удовлетво-рена, а из третьей базы не вывезены 2 ед.
Этот нераспределенный груз направляем в клетку AзBз, x зз = 2.
Потребность третьего магазина не удовлетворена на 2 ед.
Направим от фиктивного поставщика — базы А 4 — 2 ед. в клетку A 4 B 3, т.е. х 43= 2.
В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план соответствует системе ограничений транспортной задачи.
2. Подсчитаем число занятых клеток таблицы, их 7, а должно быть m + n -l = 4 + 4 –l = 7.
Следовательно, опорный план является невырожденным.
3. Определяем значение целевой функции первого опорного плана.
F( 1 ) =4*1+2*2+4*3+4*8+2*6+8*3+2*0=88 тыс.руб.
1 ) =4*1+2*2+4*3+4*8+2*6+8*3+2*0=88 тыс.руб.
4. Проверим оптимальность опорного плана.

Найдем потенциалы αi, βj по занятым клеткам таблицы, в которых αi + βj = сij, полагая, что α 1= 0, решим систему уравнений:
Занесем найденные значения потенциалов в таблицу 7.1 и вычислим оценки свободных клеток Δ ij =(βj + αi)- сij:
Δ13 = 7 + 0 - 4 = 3; Δ14 = 4 + 0 - 3 = 1;
Δ21 = 1 + 1 - 4 = -2; Δ24 = 4 + 1 - 5 = 0;
Δ31 = 1 + (-1)- 2 = -2; Δ32 = 2 + (-1) - 7 = -6;
Δ41 = 1 + (-7) -0 = -6; Δ42 = 2 + (-7) - 0 = -5;
Δ44 = 4 + (-7) –0 = -3.
Первый опорный план не является оптимальным, так как Δ13 > О и Δ14 > 0, поэтому переходим к его улучшению.
5. Выбираем максимальную оценку свободной клетки - Δ13 = 3.
Для клетки A1B3 построим цикл перераспределения груза.
Для этого в перспективную клетку A1B3 поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «—», «+», «—».
Цикл приведен в табл. 7.1.
Из чисел xij, стоящих в минусовых клетках, выбираем наименьшее, т.е. γ = min{2,4} = 2.
Прибавляем 2 к объемам грузов, стоящих в плюсовых клетках, и вычитаем 2 из xij, в минусовых клетках.
Получим новый опорный план II, в табл. 7.2.
| Bj Ai | В 1 | B2 | B3 | B4 | Запасы аi | |
| βj αi | β 1=1 | β 2=-1 | β 3=4 | β 4=1 | ||
| A 1 | α 1=О |  1
— 1
—
| ||||
| A 2 | α 2=4 | |||||
| A 3 | α 3=2 | + | — | |||
| A 4 | α 4=-4 | |||||
| Потребности bj | Σ=26 Σ=26 |
6. Определяем значение целевой функции:
F( 2 ) = F(
2 ) = F( 1 ) — γ Δ13 = 88 - 2 • 6 = 82 (тыс.руб)
1 ) — γ Δ13 = 88 - 2 • 6 = 82 (тыс.руб)
7. Количество занятых клеток в плане II - 7, следовательно, план невырожденный.
 8. Проверяем оптимальность плана методом потенциалов, для этого находим потенциалы αi, βj по занятым клеткам, где αi + βj = сij, полагая что α 1 = 0;
8. Проверяем оптимальность плана методом потенциалов, для этого находим потенциалы αi, βj по занятым клеткам, где αi + βj = сij, полагая что α 1 = 0;
Затем рассчитываем оценки свободных клеток:
Δ12 = 0 + (-1)- 2 = -3; Δ14 = 0 + 1 - 3 = -2;
Δ21 = 4 + 1 - 4 = 1; Δ24 = 4 + 1 - 5 = 0;
Δ31 = 2 + 1 - 2 = 1; Δ32 = 2 - 1 - 7 = -6;
Δ41 = -4 + 1 - 0 = -3; Δ42 =-4 - 1 - 0 = -5;
Δ44 = - 4 + + 1 - 0 = -3.
План, полученный в табл. 7.2, не оптимальный, так как Δ21 > 0 и Δ31> 0.
9. Проводим улучшение плана II путем перераспределения грузов.
В качестве перспективной клетки для загрузки выбираем A 3 B 1, в которую записываем +, затем строим цикл перераспределения, приведенный в табл.7.2.
В построенном цикле определяем величину γ =min(4,2)= 2.
Перераспределив груз, получаем новый план III, приведенный в табл. 7,3.
| Bj Ai | В 1 | B2 | B3 | B4 | Запасы аi | |
| βj αi | β 1=1 | β 2 = — 1 | β 3=4 | β 4=2 | ||
| A 1 | α 1=О |
—
 2 2
| + | |||
| A 2 | α 2=4 | |||||
| A 3 | α 3=1 | — | ||||
| A 4 | α 4=-4 | |||||
| Потребности bj | Σ=26 Σ=26 |
10. Количество занятых клеток 7, а должно быть m + n - 1 = 7, следовательно, план III невырожденный.
11. Вычислим значение целевой функции:
F( 3 ) = F(
3 ) = F( 2 ) — γ Δ31 = 82 - 2 • 1 = 80 (тыс.руб)
2 ) — γ Δ31 = 82 - 2 • 1 = 80 (тыс.руб)
12. Проверяем оптимальность плана III методом потенциалов.
 |
Находим потенциалы по занятым клеткам:
Рассчитываем оценки свободных клеток:
Δ12 = -1+ 0 - 2 = -3 Δ14 = 2 + 0 - 3 = -1
Δ21 = 1 + 4 - 4 = 1 Δ24 = 2 + 4 – 5 = 1
Δ32 = -1 + 1 – 7 = -7 Δ33 = 4 + 1 – 6 = -1
Δ41 = 1 + (-4)–0 = -3 Δ42 =-1 + (-4)–0 =-5
Δ44 = 2 + (-4)–0 = -2
План не оптимальный, так как Δ21> 0 и Δ24> 0.
13. Проводим улучшение плана III перераспределения груза.
В качестве перспективной клетки для загрузки выбираем А 2 В 1 в которую записываем +, затем строки цикл перераспределения в табл. 7.3.
Определяем величину γ = min(2; 2) = 2.
После проведения операции перераспределения получаем план IV, в табл. 7.4.
14. План получается вырожденный, поскольку в минусовых клетках цикла находятся два одинаковых минимальных объема груза, равные 2.
При перераспределении две клетки A 1 B 1и A 2 B 2 оказались свободными, поэтому число занятых клеток (6) будет меньше, чем m + n — 1 = 7.
| Bj Ai | В 1 | B2 | B3 | B4 | Запасы аi | |
| βj αi | β 1=4 | β 2 = 6 | β 3=8 | β 4=8 | ||
| A 1 | α 1=О | |||||
| A 2 | α 2=3 |

| ||||
| A 3 | α 3=1 | |||||
| A 4 | α 4=-4 | |||||
| Потребности bj | Σ=26 Σ=26 |
Для продолжения решения в одну из освободившихся клеток — в клетку A 1 B 1 записываем нуль, так как тариф с 11 меньше с 23 (с 11 ≤ с 23)
15. Вычисляем значение целевой функции:
F( 4 ) = F(
4 ) = F( 3 ) — γ Δ21 = 80 - 2 • 1 = 78 (тыс.руб)
3 ) — γ Δ21 = 80 - 2 • 1 = 78 (тыс.руб)
16. Проверяем оптимальность плана IV методом потенциалов.
 |
Находим потенциалы по занятым клеткам:
Рассчитаем оценки свободных клеток:
Δ12 = 0+ 0 - 2 = -2 Δ14 = 2 + 0 - 3 = -1
Δ23 = 4 + 3 - 8 = -1 Δ24 = 2 + 3 – 5 = 0
Δ32 = 0 + 1 – 7 = - 6 Δ33 = 4 + 1 – 6 = -1
Δ41 = 1 +(-4)–0 = -3 Δ42 = 0 +(-4)–0 = -4
Δ44 = 2 +(-4)–0 = -2
 Поскольку все оценки неположительны, меньше или равны нулю, то план IV является оптимальным, что можно представить в виде следующей матрицы:
Поскольку все оценки неположительны, меньше или равны нулю, то план IV является оптимальным, что можно представить в виде следующей матрицы:
0 0 6 0
X *4 = 2 6 0 0 F ( * 4 ) = 78 тыс. руб.
* 4 ) = 78 тыс. руб.
2 0 0 8
Анализ плана. С первой базы необходимо весь груз направить в третий магазин, со второй базы направить в первый и второй магазины в количестве 2 ед. и 6 ед., а груз с третьей базы следует вывозить в первый и четвертый магазины в количестве 2 и 8 ед. соответственно.
При этом потребность третьего магазина B 3 остается неудовлетворенной в объеме 2 ед.
Общая стоимость доставки груза потребителям будет минимальной и составляет 78 тыс.руб. Так как оценка свободной клетки Δ24 = 0, то задача имеет множество оптимальных планов.
Дата публикования: 2014-11-02; Прочитано: 788 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
