Определение ведущих столбца и строки

Из отрицательных коэффициентов индексной строки выбираем наибольший по абсолютной величине, что и определяет ведущий столбец, который показывает, какая переменная на следующей итерации перейдет из свободных в базисные.

Затем элементы столбца свободных членов симплексной таб­лицы делим на элементы того же знака (⁺/₊; ^—/_) ведущего столбца.

Результаты заносим в отдельный столбец δ i, которые будут всегда положительные.

Строка симплексной таблицы, соответствующая минимальному значению δ i является ведущей.

Она определяет пе­ременную xi которая выйдет из базиса и станет свободной.

Элемент симплексной таблицы, находящийся на пересечении ведущих столбца и строки, называют разрешающим и выделяют кружком.

Построение нового опорного плана.

Переход к новому плану осуществляется в результате пересчета симплексной таблицы мето­дом Жордана — Гаусса.

Сначала заменим переменные в базисе, т.е. вместо xi в базис войдет переменная хj соответ-ствующая ведущему столбцу.

Разделим все элементы ведущей строки предыдущей симплекс­ной таблицы на разрешающий элемент и результаты деления зане­сем в строку следующей симплексной таблицы, соответствующую введенной в базис переменной xj.

В результате этого на месте раз­решающего элемента в следующей симплексной таблице будем иметь 1, а в остальных клетках j столбца, включая клетку столбца индексной строки, записываем нули.

Остальные элементы нового плана находятся по правилу прямоугольника:

А●В

НЭ = СТЭ — ———

РЭ

где СТЭ - элемент старого плана,

РЭ - разрешающий элемент,

А, В -элементы старого плана, образующие прямоугольник с элемен­тами СТЭ и РЭ

Далее возвращаемся ко второму этапу - проверке пла­на на оптимальность.

При решении задачи линейного программирования на мини­мум целевой функции признаком оптимальности плана являются отрицательные значения всех коэффициентов индексной строки симплексной таблицы.

Если в ведущем столбце все коэффициенты aij ≤ 0, то функция цели F( ) не ограничена на множестве допустимых планов, т.е. F( ) → ¥ и задача не имеет решения.

Если в столбце δi симплексной таблицы содержатся два или несколько одинаковых наименьших значения, то новый опорный план будет вырожденным (одна или несколько базисных перемен­ных станут равными нулю).

Вырожденные планы могут привести к зацикливанию. Для выбора ведущей строки в этом случае используют метод Креко, который заключается в следующем.

Элементы строк, име­ющие одинаковые наименьшие значения δ i делятся на предпола­гаемые разрешающие элементы, а результаты заносятся в дополни­тельные строки.

За ведущую строку выбирается та, в которой рань­ше встретится наименьшее частное при чтении таблицы слева на­право по столбцам.

Например, таблица, содержащая три равных значения

δ i = 2, имеет вид:

План	Базисные перемен­ные	Значения базисных перемен­ных	xl	x2	x3	x4	x5	х6	x7	δi
II	х4									4/2=2
х5									8/4=2
х6				—1					10/5=2

Допустим, разрешающим столбцом является x 1, который вво­дится в новый план, тогда разрешающим элементом может быть: 2,4 или 5. По указанному правилу, получится таблица:

Значения базисных переменных	х1	x2	x3	х4	х5	x6	x7
		1,5		0,5
			0,25		0,25
		2,4	-0,2	0,2		0,2

Сравниваем последовательно слева направо полученные част­ные по столбцам.

В первом и втором столбцах все частные одина­ковы, а в третьем столбце наименьшее частное 1,5 в первой строке.

Следовательно, эта строка и будет разрешающей с разрешающим элементом 2.

Если в оптимальный план вошла дополнительная перемен-ная x n+ 1, то при реализации такого плана имеются недоиспользован­ные ресурсы i -го вида в количестве, полученном в столбце свобод­ных членов симплексной таблицы.

Если в индексной строке симплексной таблицы оптимального плана находится нуль, принадлежащий свободной переменной, не вошедшей в базис, а в столбце, содержащем этот нуль, имеется хотя бы один положительный элемент, то задача имеет множество опти­мальных планов.

Свободную переменную, соответствующую ука­занному столбцу, можно внести в базис, выполнив соот-ветствую­щие этапы алгоритма.

В результате будет получен второй оптималь­ный план с другим набором базисных переменных.

Пример 1. Коммерческое предприятие, реализует три группы товаров А, В и С.

Нормативы затрат ресурсов на 1 тыс.руб. товарообо­рота, доход от продажи товаров на 1 тыс.руб. товарооборота, а также объем ресурсов заданы в табл. 4.1.

Виды материально-денежных ресурсов	Норма затрат материально-денежных ресурсов на 1 тыс.руб. товарооборота	Объем ресурсов bi
группа А	группа В	группа С
Рабочее время продав­цов, чел.-ч	0,1	0,2	0,4
Площадь торговых за­лов, м2	0,05	0,02	0,02
Площадь складских помещений, м2
Доход, тыс. руб.				max

Определить объем продажи и структуру товарообо­рота так, чтобы доход торгового предприятия был максимальный.

Решение. Запишем математическую модель задачи.

Определим вектор =(x1,x2,x3), который удовлетворяет усло­виям

0,1 x ₁ + 0,2 x₂ + 0,4 x₃ £1100

0,05 x ₁ + 0,02 x₂ + 0,02 x₃ £120

3 x ₁ + x₂ + 2 x₃ £ 8000

x ₁³ 0, x₂ ³ 0, x₃ ³0

и обеспечивает максимальное значение целевой функции

F(X) = З x ₁ + 5 х ₂ + 4 х ₃ -> max.

Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных x_4, х₅, х₆.

0,1 x ₁ + 0,2 x₂ + 0,4 x₃ + x ₄ =1100

0,05 x ₁ + 0,02 x₂ + 0,02 x₃ + x ₅=120

3 x ₁ + x₂ + 2 x₃ + x ₆= 8000

Матрица коэффициентов А =(aij) этой системы уравнений имеет следующий вид:

0,1 0,2 0,4 1 0 0

A = 0,05 0,02 0,02 0 1 0

3 1 2 0 0 1

Векторы , , - линейно независимы, так как определи­тель, составленный из компонент этих векторов, отличен от нуля.

Следовательно, соответствующие этим векторам переменные x₄,x₅,x₆ являются базисными и в этой задаче определяют объемы неис­пользованных ресурсов.

Решим систему уравнений относительно базисных переменных.

x₄ = 1100 — (0,1 x ₁ + 0,2 x₂+ 0,4 x₃ + x ₄)

x₅ = 120 — (0,05 x ₁ + 0,02 x₂+ 0,02 x₃ + x ₅)

x₆ = 8000 — (3 x ₁ + x₂+ 2 x₃ + x ₆)

Функцию цели запишем в виде уравнения:

F(X) = 0 —(З x ₁ — 5 х ₂ — 4 х ₃).

Полагая, что свободные переменные x ₁ =0, х ₂ =0, х ₃ =0, полу­чим первый опорный план 1 =(0,0,0.1100,120,8000), F( ) = О, в котором базисные переменные x ₄ = 1100, x ₅ = 120, x ₆ = 8000.

Сле­довательно, товары не продаются, доход равен нулю, а ресурсы не используются.

Полученный первый опорный план запишем в симп­лексную таблице 4.2.

План	Базисные перемен­ные	Значения базисных переменных	Значения коэффициентов при переменных	δi
x 1	x 2	x 3	x 4	x 5	x 6
I	x 4 x 5 x 6		0,1 0,05	0,2 0,02	0,4 0,02
Индекс­ная строка	F( )		-3	-5	-4
II	x 2 x 5 x 6		0,5 0,04 2,5		-0,02	-0,1 -5
Индекс­ная строка	F( )		-0,5
III	x 2 x 1 x 6				2,25 -0.5 1,25	6,25 -2,5 1,25	12,5 -62,5
Индекс­ная строка	F( )				5,75	23,75	12,5

Первый опорный план неоптимальный, так как в индексной строке находятся отрицательные коэффициенты: — 3, — 5, — 4.

За ведущий столбец выберем столбец, соответствующий пере­менной x ₂, так как, сравнивая по модулю, имеем:

|-5| > {|-3|,|-4|}.

Вычислим значения δ i по строкам как частное от деления bi / ai 2 и выбираем наименьшее:

min δ i =min(bi / ai 2)=min[1100/0.2;120/0.02;8000/1]=5500

Следовательно, первая строка является ведущей.

Разрешающий элемент равен 0,2 и находится на пересечении ведущего столбца и ведущей строки и выделен в таблице.

Формируем следующую часть симплексной таблицы.

Вместо переменной x4 в план II войдет переменная x2.

Строка, соответст­вующая переменной х2 в плане II, получена в результате деления всех элементов строки х 2 плана I на разрешающий элемент РЭ = 0,2.

На месте разрешающего элемента в плане II получаем 1.

В остальных клетках столбца x ₂ плана II записываем нули.

Таким образом, в новом плане II заполнены строки x ₂ и столбец x ₂.

Все остальные элементы нового плана II, включая элементы индексной строки, определяются по правилу прямоугольника.

Для этого выбираем из старого плана четыре числа, которые располо­жены в вершинах прямоугольника и всегда включают разрешаю­щий элемент РЭ = 0,2.

Во второй вершине по диагонали находится старое значение элемента, например, значение целевой функции F(K ₁ ) = 0 = СЭ, которое указывает на место расположения нового НЭ в новом плане II.

Третий элемент А = 1100 и четвертый элемент В = -5 завершают построение прямоугольника в недостающих двух вершинах и расположены по другой диагонали.

Значение нового элемента в плане II находится из выражения:

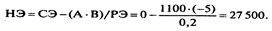
Элементы строки определяются аналогично:

1100·0,02 0,1·0,02

120 - ——————————— = 10 0,05 - —————————— = 0,04

0,2 0,2

0,4·0,02 0,02·1

0,02 - —————————— = — 0,02 0 — —————————— = — 0,1

0,2 0,2

Все элементы, расположенные на пересечении строк и столб­цов, соответствующих одноименным базисным элементам, равны 1.

Остальные элементы столбца в базисах векторов, включая индекс­ную строку, равны 0.

Аналогично проводятся расчеты по всем стро­кам таблицы, включая индексную.

Выполняя последовательно все этапы алгоритма, формулируем план II.

На третьей итерации табл.4.2 получаем план III, который явля­ется оптимальным, так как все коэффициенты в индексной строке ≥ O.

Оптимальный план можно записать так:

*= (250,5375,0,0,0,1875), F( ) = 27 625 тыс.руб.

Следовательно, необходимо продавать товаров первой группы А 250 ед., а второй группы В - 5375 ед.

При этом торговое предпри­ятие получает максимальный доход в размере 27 625 тыс.руб.

То­вары группы С не реализуются,

В оптимальном плане среди базисных переменных находится дополнительная переменная x ₆.

Это указывает на то, что ресурсы третьего вида (площадь складских помещений) недоиспользована на 1875 м², так как переменная х ₆ была введена в третье ограниче­ние задачи, характеризующее собой использование складских по­мещений этого ресурса.

В индексной строке оптимального плана в столбцах перемен­ных x ₃, x ₄, x ₅, не вошедших в состав базисных, получены ненулевые элементы, поэтому оптимальный план задачи линейного програм­мирования является единственным.

Пример 3. Рассмотрим решение задачи ЛП с учетом дополнительных ограничений другого вида ≥:

0,5 x н +x в ≤ 3 0,5 x н + x в + x 1 = 3

x н + 0,5 x в ≤ 4 x н + 0,5 x в + x 2 = 4

— x н +x в ≤ 1,5 — x н + x в + x 3 = 1,5

x в ≤ 2 x в + x 4 = 2

x в ≥ 0,25 x в + x 5 = 0,25

x н ≥ 0,5 x н + x 6 = 0,5

F(X)=2 x н + 3 x в → max F(X)=0–(-2 x н - 3 x в)→ max

Заполним симплексную таблицу 4.4 и проведем соответствую­щие операции, учитывая, что при вычислении частных δ i, необхо­димо деление проводить только с числами одинакового знака.

План	Базис­ные пе­ремен­ные	Значе­ния ба­зисных пере­менных	x н	x в	x 1	x 2	x 3	x 4	x 5	x 6	δi
I	х 1		0,5
x 2			0,5
х 3	1,5	-1								1,5
x 4
x 5	-1/4		-1							1/4
x 6	-0,5	-1								-
F(X)		-2	-3
VI	х 3	3,5			-2
x 4	2/3			-4/з	2/з
x 5	11/12			4/з	-2/з
x н	З1/з			-2/з	4/з
x в	l1/з			4/з	-2/з
x 6	25/6			-2/з	4/з
F(X)	102/з			22/з	2/з

После нескольких итераций, часть которых в таблице пропу­щена, получим оптимальный план

* = (3¹/₃; 1¹/₃; 0; 0; 3,5; ²/₃; 1¹/₁₂; 2⁵/₆)

Решение задачи закончено F(X ₆ ) = 10 ²/₃ тыс.руб.