Приведем еще один пример. Пусть некоторая техническая система состоит

из n устройств (станки, подающие механизмы, элементы системы энергоснабжения и т.п.) и пусть эта система не может выполнять функции, если неисправно любое одно устройство. Тогда такая система имеет n+1 состояние: Z₀ - все устройства исправны; Z_i, i=1, n,-i-ое устройство отказало и находится в ремонте, а все остальные устройства исправны.

Совокупность технических устройств и бригады ремонтников можно рассматривать как систему массового обслуживания. Отказы технических устройств здесь образуют поток заявок на обслуживание, а бригады ремонтников являются обслуживающим устройством.

Процесс функционирования можно считать марковским с дискретными состояниями и непрерывным временем. Действительно здесь состояния Z₀,Z₁,Z₂,...,Z_n можно заранее перечислить, а переход системы из состояния в состояние происходит мгновенно в случайные моменты времени. Кроме того, вероятностные характеристики обслуживания отказавших устройств можно считать зависящими лишь от состояния системы в момент t₀ и независящими от предыстории ее функционирования.

Функционирование СМО удобно описывать с помощью ориентированного графа, вершины которого соответствуют состояниям системы Z₁,Z₂,...,Z_n, а дуги – переходам из состояние в состояние.

В случае обслуживания пользователей двумя ЭВМ граф состояний будет иметь вид, показанный на рис.3.1. Из состояния Z₀, когда заявка на обслуживание отсутствует и обе ЭВМ простаивают, возможны два перехода в случайные моменты времени - переход в состояние Z₁, когда первая ЭВМ занята обслуживанием пользователя, а вторая - свободна, и в состояние Z₂, когда вторая ЭВМ занята, а первая - свободна. Из состояний Z₁ и Z₂ возможны два переход: в состояние Z₀, когда пользователь обслужен, а новая заявка на обслуживание не поступила, и в

состояние Z₃, когда заявка ЭВМ еще не обслужена, а появилась новая заявка В состоянии Z₃ образована очередь на обслуживание пользователей. Из состояния Z₃ возможны переходы либо

Рис.3.1. в состояние Z₁, либо в состояние Z₂, когда первая или вторая ЭВМ обслуживают лишь одного из пользователей, и очереди нет. Конечно, из состояния Z₃ возможны и другие переходы, если пользователи с высокой интенсивностью приходят в вычислительный центр, и длина очереди растет. Однако, в данном примере не рассматриваются закономерности образования очереди.

На графе рис.3.1 отсутствует переход из состояния Z₀ в состояние Z₃. Если поток заявок является ординарным, то вероятность поступления одновременно более одной заявки теоретически равна 0, а это означает, что переход из Z₀ в Z₃ невозможен. Часто на графе состояний указываются интенсивности переходов. В нашем случае на рисунке обозначены: λ - интенсивность поступления заявок, μ₁ - интенсивность обслуживания пользователя первой ЭВМ, μ₂ - интенсивность обслуживания пользователя второй ЭВМ.

На рис.3.2. приведен граф состояний СМО, состоящий из n технических устройств и ремонтной бригады. В этом примере состояние Z₀ - все устройства исправны. Из этого состояния система в случайные моменты времени может перейти с интенсивностью λ1,λ2,...,λ_n соответственно в состояние Z₁, Z₂,…

Рис.3.2 Z_n. В состоянии Z_i, i=1,n i-ое устройство отказало и ремонтируется, остальные устройства исправны, но вся система без i-го устройства не работает. Из i-го отказового состояния Z_i система с интенсивностью восстановления μ_i, i=1,n может вернуться в работоспособное состояние Z₀, когда все устройства исправны. В этой модели функционирования СМО предполагается, что в течение времени ремонта отказавшего устройства другие устройства не работают, и отказать не могут, то есть поток отказов ординарный.

Таким образом, для описания мартовской системы необходимо:

1) определить понятие состояния системы; состояния могут быть

связаны с числом заявок, находящихся в системе с моментами

обработки заявок и т.п.;

2) определить количество все возможных состояний

3) задать начальное состояние Z₀;

4) построить граф состояний;

5)
задать интенсивности переходов между всем состояниями:
где P_ij – вероятность перехода из состояния Z_i в Z_j.

Исчерпывающей характеристикой систем массового обслуживания описанного типа являются вероятности всевозможных состояний, системы для определения которых составляются система линейных дифференциальных уравнений с постоянными коэффициентами.

Способы составления уравнений рассматриваются на примере.

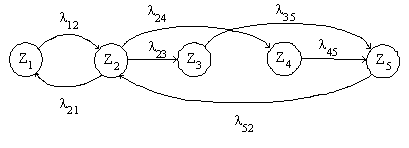Пусть имеется система массового обслуживания, множество состояний которой и переходы можно представить в виде графа на рис.3.3.

Рис.3.3.

Вероятность нахождения системы в состоянии Z_i обозначается P_i(t); интенсивности переходов между состояниями Z_i и Z_j – λ_ij(i,j = 1,n).

Определим вероятность нахождения системы в состоянии Z₂ - P₂(t); для чего рассмотрим промежуток времени от t до t + ∆t и вычислим вероятность того, что в конце этого промежутка система будет находится в состоянии Z₂. Это может произойти в следующих случаях:

a) в момент времени t система находилась в состоянии Z₂ и за время ∆t не вышла из этого состояния;

b) в момент времени t система находилась в состояниях Z₁ и Z₅, но за время ∆t перешла в состояние Z₂.

Вычислим вероятности событий a) и b). Вероятность P₂(t + ∆t), будет равна произведению вероятностей пребывания системы в момент времени t в состоянии Z₀ и вероятности того, что за ∆t она не выйдет из этого состояния:

где

Вероятность события b) равна сумме вероятностей перехода системы из состояний Z₁ Z₅:

Суммарная вероятность P₂(t + ∆t), будет равна:

Образовав в левой части (3.1) конечную разность и устремив ∆t к нулю, получим:

Аналогично можно получить производные вероятностей и остальных состояний:

Таким образом получена система дифференциальных уравнений, решив которую, можно определить вероятности всевозможных состояний системы. Обобщая уравнения системы, можно записать:

Уравнения можно написать, не прибегая к выводу, непосредственно по графу состояний, если использовать следующее правило: в левой части каждого из уравнений стоит производная вероятности i-го состояния; в правой части - сумма произведений вероятностей состояний, из которых выходят стрелки в данное состояние, на интенсивности соответствующих переходов, минус произведение суммарной интенсивности перехода из i-го состояния на вероятность этого состояния.

Пользуясь этим правилом, можно записать систему уравнений СМО, граф состояний которой изображен на рис.3.1. Обозначим P₀(t), P₁(t), P₂(t), P₃(t) - вероятности пребывания системы в момент времени t соответственно в состояниях Z₀, Z₁, Z₂, Z₃. Тогда система уравнений будет иметь вид:

Решение дифференциальных уравнений возможно, если известны начальные условия функционирования системы. Часто можно рассматривать работу системы с момента времени, когда она свободна от заявок. Тогда за начальные условия принимаются: P₀(0) = 1, P₁(0) = P₂(0) =... = P_n(0) = 0.

Уравнения вида (3.1), (3.2) и (3.3) называют уравнениями А.Н.Колмогорова, по имени выдающегося советского математика.

Важным свойством уравнение Колмогорова является следующее: сумма правых частей уравнения равна нулю.Это свойство можно использовать при проверке правильности написания уравнений.

Можно доказать, что для системы в стационарном состоянии вероятности состояний имеют предельные значения, не зависящие от начального состояния системы, то есть

limP_i(t) = P_i , i=1,n, (3.4)

^t→∞

где P_i – финальные вероятности.

Это означает, что при определении финальных вероятностей следует все производные в левой части уравнений Колмогорова принять равным нулю. Тогда система дифференциальных уравнений превращается в систему линейных алгебраических уравнений.

Для случайной системы, граф состояний которой приведен на рис.3.1., система уравнений имеет вид:

Однородные уравнения (3.5) и (3.6) можно решить, используя уравнение, называемое нормировочным (сумма вероятностей всех состояний равна единице): для случая уравнений (3.6)

P₀+P₁+P₂+P₃ = 1

Теперь можно одно любое уравнение системы исключить и заменить его нормировочным. Система будет иметь единственное решение. Смысл финальных вероятностей становится понятным, если их интерпретировать как средние относительные времена пребывания системы в соответствующих состояниях. Например, если в первом примере Р₀=0.2; P₁=0.25; P₂=0.25; P₃=0.3, то это значит, что исследуемая СМО находится в состоянии Z₀ в среднем две десятых времени, в состояниях Z₁ и Z₂ - по одной четверти времени и в состоянии Z₃ - три десятых суммарного времени.

Зная финальные вероятности всех состояний СМО, можно найти ряд других важных показателей ее эффективности.

Часто в системах массового обслуживания интересуются не вероятностью пребывания в момент времени t в состоянии Z_i, а вероятностью того, что в течение времени t система попадает (или не попадает) в это состояние. Тогда для определения P_i(t) следует считать, что процесс обслуживания закончен, если система попала в состояние Z_i, т.е. считать, что переходы из i-го состояния в другие состояния невозможны ("экран" для соответствующих ветвей на графе состояний).

Пусть, например, нужно определить вероятность того, что техническая система, граф состояний которой изображен на рис.3.2., не откажет в течение времени ∆t, т.е. ни одно из устройств системы не попадет на обслуживание в ремонтную бригаду. Из графа видно, что в поставленной задаче необходимо определить вероятность P₀(t) пребывания системы в состоянии Z₀ в течение времени t.

Если же система попадет в одно из состояний Z₁,Z₂,...,Z_n, то произойдет ее отказ. Очевидно, что для определения P₀(t) необходимо в графе состояний запретить переходы в Z₀ из состояний Z₁,Z₂,...Z_n. На графе это отмечено пунктирными линиями ("экраны"). Тогда система дифференциальных уравнений примет вид:

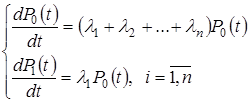При начальных условиях P₀(0) = 1, P_i(0) = 0,

P₀(t) = e^-λt,

где λ = λ₁ + λ₂ +... +λ_n - интенсивность отказа системы.