Лекція 2. Режими роботи електричних кіл. Розрахунок кіл постійного струму

План

· Режими роботи електричних кіл.

q Режими роботи електричних кіл та відповідні їм точки на зовнішній характеристиці генератора.

q Джерело ЕРС. та джерело струму.

· Розрахунок кіл постійного струму.

q Способи з’єднання споживачів і джерел.

q Розрахунок простих кіл

q Закони Кірхгофа.

q Перетворення трикутника опорів в еквівалентну зірку.

Режими роботи електричних кіл.

Із всіх режимів роботи електричних кіл та окремих їх елементів найхарактернішими є:

§ номінальний режим;

§ узгоджений режим;

§ режим холостого ходу (х.х.);

§ режим короткого замикання (к.з.).

Номінальним називається режим роботи, для якого розраховане джерело електричної енергії або електроприймач.

Для електричних величин, що визначають номінальний режим, відносяться номінальна напруга, номінальний струм, номінальна потужність.

Генератори, електроприймачі та інші елементи електричних установок виробляють не на будь–які напруги, а на обмежене число визначених напруг. Шкала цих напруг, які прийнято називати номінальними, встановлюються державним стандартом.

Номінальний режим джерела або споживача електроенергії вказується в паспорті на цей елемент. Номінальні значення струму І _ном, напруги U _ном і потужності Р _ном відповідають найвигіднішим умовам роботи пристрою з точки зору економічності, надійності, довговічності та ін.

Узгодженим називається режим, при якому джерело віддає в зовнішнє коло найбільшу потужність Р _mах.

Покажемо, що такий режим досягається, коли зовнішній опір кола R _зовн дорівнює внутрішньому опору джерела R _дж.

Потужність, що віддає джерело дорівнює .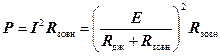

Щоб знайти максимальне значення функції P (R _зовн) прирівняємо нулю похідну = 0:

Останнє отримане співвідношення є умовою отримання максимуму функції P (R _зовн) тому, що:

Коефіцієнт корисної дії джерела h =Р _зовн / Р, тобто відношенню потужності, що споживається зовнішнім колом, до потужності, що віддає джерело, і при довільному значенні R _зовн складає .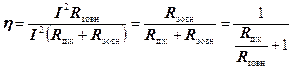

При узгодженому режимі джерело працює з к.к.д. .

Найбільша потужність, що віддається джерелом при узгодженому режимі складає .

Режими холостого ходу і короткого замикання.

Граничними режимами роботи джерела є:

§ режим холостого ходу – зовнішнє коло розімкнене;

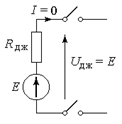§ режим короткого замикання – клеми джерела замкнені провідником, опір якого нескінченно малий.

В режимі холостого ходу, тобто при розімкненому зовнішньому колі, його опір практично дорівнює нескінченності (R _зовн = ¥), а величина струму дорівнює нулю (І = 0). Так як в цьому випадку падіння напруги всередині джерела дорівнює нулю, то напруга на клемах джерела дорівнює ЕРС (U _дж = Е).

Коротке замикання виникає в результаті пошкодження ізоляції струмоводних частин. Чим ближче до джерела місце короткого замикання, тим менший опір контуру abcda і тим більше величина струму короткого замикання І _кз. При короткому замиканні на клемах джерела зовнішній опір близький до нуля, струм джерела досягає найбільшого значення , обмежується тільки опором джерела R _дж і може в багато разів перевищувати номінальний струм навантаження. Напруга на клемах джерела U _дж при цьому дорівнює нулю.

Коротке замикання є великою небезпекою для електричних установок. Для запобігання цього аварійного режиму використовують плавкі запобіжники (З).

Точки характерних режимів на зовнішній характеристиці джерела.

Вираз U _дж = Е – R _дж І (див. п° 1.3) є рівнянням зовнішньої характеристики джерела, що описує залежність напруги в зовнішньому колі від струму в ньому. При умові Е = const і R _дж = const залежність U _дж(І) є лінійною.

На графіку зовнішньої характеристики буквами позначені:

Н – область, що відповідає номінальному режиму;

У – точка, що відповідає узгодженому режиму;

ХХ – точка, що відповідає режиму холостого ходу;

КЗ – точка, що відповідає режиму короткого замикання.

Джерело ЕРС та джерело струму.

При аналізі та розрахунку електричних кіл джерело електроенергії з параметрами – ЕРС Е і внутрішнім опором R _дж – може бути представлене двома способами: як джерело ЕРС або як джерело струму.

Джерелом ЕРС називається джерело електроенергії, внутрішній опір якого R _дж дуже малий, так що напруга на клемах джерела U _дж = Е – R _дж І при зміні струму в межах від нуля до номінального І _ном змінюється незначно.

До джерел ЕРС можна віднести електромеханічні генератори, гальванічні елементи, акумулятори, для яких R _зовн>> R _дж.

Ідеальним джерелом ЕРС називається умовне джерело, напруга на якому не залежить від струму в навантаженні і дорівнює ЕРС (внутрішній опір R _дж =0).

Зовнішня характеристика ідеального джерела ЕРС і його позначення на схемах має вигляд:

До джерел струму відносять джерела електроенергії з великим внутрішнім опором R _дж, в яких струм І кола практично не залежить від значення напруги U на приймачі при його змінах від 0 до номінального.

Ідеальним джерелом струму називається джерело електроенергії, струм якого не залежить від значення напруги U (або опору приймача R _н) і дорівнює струму короткого замикання джерела живлення – І _кз = Е / R _дж.

Схема заміни реального джерела ЕРС складається з ідеального джерела ЕРС і послідовно з’єднаного з ним опору R _дж реального джерела електроенергії.

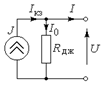
Схема заміни реального джерела струму складається з ідеального джерела струму і паралельно включеного з ним резистивним елементом, опір якого дорівнює внутрішньому опору R _дж реального джерела електроенергії.

Найбільш вживаною є послідовна схема заміни джерела, так як вона більше відповідає потужним джерелам.

Схема заміни з джерелом струму частіше вживається для аналізу і розрахунку електричних кіл в електроніці, автоматиці, радіотехніці.

Щоб замінити схему з джерелом струму з параметрами J і R _дж схемою з джерелом ЕРС треба покласти значення Е = J× R _дж.

Розрахунок кіл постійного струму.

Способи з’єднання споживачів

Приймачі енергії можна з’єднувати послідовно, паралельно і змішано.

При послідовному з’єднані умовний кінець першого приймача з’єднується з умовним початком другого, кінець другого – з початком третього і т.д.

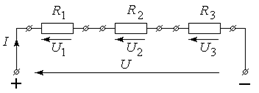На малюнку приймачі з опорами R ₁, R ₂, R ₃ з’єднані послідовно і підключені до джерела енергії з напругою U. По всім ділянкам послідовного кола проходить один і той же струм І. За законом Ома напруга на окремих опорах:

U ₁ = IR ₁; U ₂ = IR ₂; U ₃ = IR ₃.

Отже, падіння напруги на послідовно з’єднаних опорах пропорційні величинам опорів. При послідовному з’єднані приймачів сума напруг на окремих приймачах дорівнює напрузі на клемах кола, тобто U ₁ + U ₂ + U ₃ = U.

Ряд послідовно з’єднаних приймачів можна замінити еквівалентним (загальним) опором R. Величина цього опору повинна бути такою, щоб ця заміна при незмінній напрузі на клемах кола U не викликала зміну струму І в колі. Оскільки U ₁ + U ₂ + U ₃ = U; U ₁ = IR ₁; U ₂ = IR ₂; U ₃ = IR ₃, то IR = IR ₁ + IR ₂ + IR ₃. Після скорочення на І отримаємо R = R ₁ + R ₂ + R ₃.

Отже при послідовному з’єднані еквівалентний опір дорівнює сумі опорів окремих елементів, що входять до з’єднання.

Якщо всі елементи рівняння U ₁ + U ₂ + U ₃ = U помножити на струм І, то отримаємо ІU ₁ + ІU ₂ + ІU ₃ = ІU або Р ₁ + Р ₂ + Р ₃ = Р.

Тобто потужність всього кола Р дорівнює сумі потужностей окремих його ділянок.

При паралельному з’єднані приймачів всі вони знаходяться під однаковою напругою U.

Позначимо опори окремих приймачів R ₁, R ₂, R ₃; їх провідності – g ₁, g ₂, g ₃; струми – І ₁, І ₂, І ₃. Загальний струм І в нерозгалуженій частині кола дорівнює сумі струмів, що споживаються окремими приймачами:

І = І ₁ + І ₂ + І ₃ = U / R ₁ + U / R ₂ + U / R ₃ = U (1 / R ₁ + 1 / R ₂ + 1 / R ₃) = U / R _е

або

І = U g ₁ + U g ₂ + U g ₃ = U (g ₁ + g ₂ + g ₃) = U g _е.

Отже еквівалентна провідність розгалуженого кола дорівнює сумі провідностей окремих його віток:

1 / R ₁ + 1 / R ₂ + 1 / R ₃ = 1 / R _е або g ₁ + g ₂ + g ₃ = g _е.

В окремому випадку, коли коло містить два паралельно включених опора R 1 і R 2, еквівалентний опір R е зручно визначати за формулою .

Якщо вираз U / R ₁ + U / R ₂ + U / R ₃ = U / R _е помножити на U отримаємо U ² / R ₁ + U ² / R ₂ + U ² / R ₃ = U ² / R _е або Р ₁ + Р ₂ + Р ₃ = Р.

З викладеного слідує, що потужність, споживана розгалуженим колом, дорівнює сумі потужностей, споживаних окремими приймачами або одним еквівалентним приймачем. Провідність еквівалентного приймача дорівнює сумі провідностей всіх паралельно включених приймачів. Струми в цих приймачах так, як і потужності, розподіляються завжди пропорційно провідностям.

Якщо електричне коло уявляє собою поєднання послідовно і паралельно включених споживачів, то схема з’єднань називається змішаною.

З’єднання елементів живлення.

Кількість електрики, яку можна отримати від елемента живлення під час його розряду, називається ємкістю елемента. Ємкість вимірюється в ампер–годинах (А×год.) і визначається за формулою Q = I _р t _р, де I _р – розрядний струм, t _р – час розряду. Чим більше активних речовин в елементі, тим більша його ємкість. Кожний елемент характеризується також допустимим розрядним струмом.

Первинні елементи і акумулятори мають порівняно низьку ЕРС. Наприклад:

§ Марганцево–цинкові і повітряно–марганцево–цинкові елементи – 1,5 В;

§ Ртутно–цинкові елементи – 1,35 В;

§ Кислотні акумулятори – 2 В;

§ Лужні акумулятори – 1,4 В.

Допустимий розрядний струм акумуляторів великої ємкості досягає кількох сотень ампер.

Елементи з великим внутрішнім опором можуть розряджатись невеликими струмами.

Між тим часто для роботи споживачів енергії потрібні напруга U іструм І більшого значення, ніж може дати один елемент. В таких випадках однорідні елементи, що мають однакові ЕРС Е _е, ємкість Q _е і внутрішній опір R _е, з’єднуються в батареї. Використовуються три способи з’єднання елементів в батареї: послідовний, паралельний і змішаний. Для вибору способу з’єднання необхідно знати номінальну напругу U і потужність Р приймача енергії. За цими даними можна визначити струм приймача І = Р / U і його опір R = U / І.

Послідовне з’єднання елементів.

Якщо номінальна напруга приймача більша за напругу одного елемента, а його струм не перевищує допустимого розрядного струму одного елемента, то застосовують послідовне з’єднання елементів. При цьому позитивний полюс першого елемента з’єднують з від’ємним полюсом другого, позитивний полюс другого – з від’ємним полюсом третього і т.д. Від’ємний полюс першого і позитивний полюс останнього елементу є полюсами створеної таким чином батареї.

ЕРС батареї, так як ЕРС елементів направлені в один бік, дорівнює Е = Е _1е + Е _2е + … + Е _nе = nE _е . аналогічно R = nR _е.

При послідовному з’єднані всі елементи розряджаються і заряджаються однаковим струмом. Тому ємкість батареї Q дорівнює ємкості одного елемента Q _е (Q = Q _е).

Паралельне з’єднання елементів.

В тих випадках, коли номінальна напруга приймачів енергії дорівнює напрузі одного елемента, а його струм більший за допустимий розрядний струм одного елемента, застосовують паралельне з’єднання елементів.

При цьому позитивні полюси окремих елементів з’єднуються в один вузол, а від’ємні – в інший. До вузлових точок приєднують приймач з опором R. ЕРС батареї при паралельному з'єднані дорівнює ЕРС одного елемента Е = Е _е. Внутрішній опір батареї дорівнює опору одного елемента поділеному на кількість елементів в батареї R _вн = R _е / m. Якщо розрядний струм одного елемента І _е, то батарея може забезпечити струм до І = mІ _е. Ємкість батареї дорівнює сумі ємкостей паралельно з’єднання елементів.

Отже, при паралельнім з'єднані збільшується розрядний струм і ємкість батареї, а її внутрішній опір зменшується. Всі паралельно з’єднані елементи повинні мати однакові ЕРС і внутрішній опір, інакше елементи з меншим ЕРС будуть споживачами енергії. При однакових ЕРС елементи з меншим опором розрядяться швидше елементів з більшим внутрішнім опором.

Змішане з’єднання елементів.

Змішане з’єднання елементів застосовується для збільшення напруги і ємкості батареї.

Е = nЕ _е; R _вн = nR _е / m; І = mІ _е, де

n – кількість елементів однієї вітки батареї, з’єднаних послідовно;

m – кількість віток батареї.

Розрахунок простих кіл електричного струму.

Головною задачею розрахунку електричних кіл є визначення струмів і потужностей в різних елементах кола (джерелах, приймачах, проводах), а також напруги на окремих елементах кола.

Вихідними даними для розрахунку звичайно є задані ЕРС кола і характеристики (параметри) елементів кола, тобто або їх опори, або номінальні напруги і потужності.

Якщо діюча в колі ЕРС і параметри елементів незмінні в часі, то така задача має однозначне рішення.

Якщо електричне коло уявляє собою поєднання послідовно і паралельно включених споживачів (змішана схема з’єднань) і при цьому має одне джерело живлення (одну ЕРС), то вона розраховується в такому порядку:

1. Шляхом послідовного спрощення знаходять загальний опір кола.

2. За законом Ома знаходять загальний струм.

3. Знаходять розподіл струмів і напруг в схемі.

Методику розрахунку розглянемо на прикладі.

Вихідні дані:

U = 240 В; R ₁ = 10 Ом; R ₂ = 20 Ом; R ₃ = 60 Ом; R ₄ = 9 Ом; R ₅ = 30 Ом; R ₆ = 4 Ом; R ₇ = 2 Ом.

Знайти розподіл струмів в схемі.

Розрахунок:

Визначаємо еквівалентний опір між точками АВ:

.

Складаємо послідовно з’єднані опори R _АВ та R ₄ і отримаємо R ¢:

R ¢ = R _АВ + R ₄ = 6 + 9 = 15 Ом.

Опір R ¢ в свою чергу виявляється з’єднаним паралельно з опором R ₅. Їх загальний опір:

.

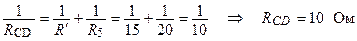Загальний опір кола:

R = R ₆ + R _CD + R ₇ = 4 + 10 + 2 = 16 Ом.

Загальний струм:

I = U / R = 240 / 16 = 15 A.

Напруга між точками C і D:

U _CD = I×R _CD = 15 × 10 = 150 B.

Струми в опорах R ¢ і R ₅:

I ₄ = U _CD / R ¢ = 150 / 15 = 10 A; I ₅ = U _CD / R ₅ = 150 / 30 = 5 A.

Напруга між точками А і В:

U _AB = I ₄ ×R _AB = 10 × 6 = 60 В.

Струми в опорах R ₁, R ₂, R ₃.

I ₁ = U _АВ / R ₁ = 60 / 10 = 6 A;

I ₂ = U _АВ / R ₂ = 60 / 20 = 3 A;

I ₃ = U _АВ / R ₃ = 60 / 60 = 1 A.

Для перевірки розрахунку можна використати те, що в електричному колі завжди встановлюється струм І такої величини, при якій загальна потужність, що віддається джерелом дорівнює сумі потужностей, що споживаються кожним приймачем кола.

Необхідно звернути увагу на те, що в електричному колі завжди встановлюється струм І такої величини, при якій прикладена до кола напруга U повністю врівноважує (компенсує) втрати напруги в усіх послідовно включених елементах кола. Зміна величини опору будь–якої ділянки схеми неминуче спричиняє зміну як загального струму, так і струмів, що протікають в окремих елементах цієї схеми.

Розрахунок складних кіл.

Закони Кірхгофа.

До вузлів схеми застосовується перший закон Кірхгофа: сума струмів, що притікають до будь–якої точки розгалуження (вузлу), дорівнює сумі струмів, що відходять від неї. Якщо струми, що притікають до точки, вважати додатними, а такі, що відходять від неї, – від’ємними, то перший закон Кірхгофа можна сформулювати так: алгебраїчна сума струмів у вузловій точці дорівнює нулю – S І = 0.

Згідно другого закону Кірхгофа, в усякому замкнутому контурі алгебраїчна сума ЕРС дорівнює алгебраїчній сумі падінь напруг на всіх опорах, що включені в цей контур: S Е = S ІR.

Розглянемо схему

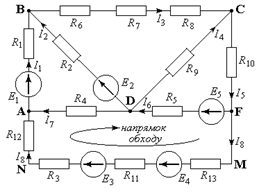Вузли схеми: A, B, C, D, F.

Вітки: AB, BC, CD, BD, CF, AD, DF, ANMF.

Контури: ABDA, BCDB, CDFC, ADFMNA.

Перший закон Кірхгофа, наприклад, для вузла А визначається рівнянням: І ₇ + І ₈ – І ₁ = 0.

Другий закон Кірхгофа, наприклад, для контуру ADFMNA визначається рівнянням:

І ₈ R ₁₂ – І ₇ R ₄ – І ₆ R ₅ + І ₈ R ₁₃ + І ₈ R ₁₁ + І ₈ R ₃ = – E ₅ + E ₄ + E ₃.

При складанні рівнянь за другим законом Кірхгофа і обході замкнутого контуру ЕРС і струми, напрямки яких співпадають з прийнятим напрямком обходу – за годинниковою стрілкою (або проти), треба вважати додатними, а ЕРС і струми, напрямки яких протилежні напрямку обходу – від’ємними.

Перетворення трикутника опорів в еквівалентну зірку.

При розрахунку електричних кіл, які не вдається звести до одного результуючого опору шляхом заміни послідовно і паралельно з’єднаних опорів їх еквівалентними величинами доводиться вдаватись до більш складних перетворень. Зокрема, якщо в колі зустрічається замкнутий контур з трьох опорів R _AB, R _BC, R _CA, що утворюють сторони трикутника, то ці опори заміняють трьома опорами R _A, R _B, R _C, що з’єднані в одній вузловій точці О і утворюють трипроменеву зірку (D ® U).

При такому перетворенні опір між точками А і В, В і С та С і А повинні бути однаковими в обох видах з’єднання:

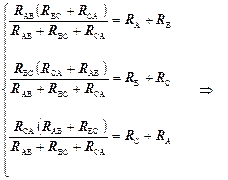
Аналогічно

При зворотному переході від зірки опорів до еквівалентного трикутника опорів (U®D) опори R _AB, R _BC, R _CA визначаються через опори R _A, R _B, R _C:

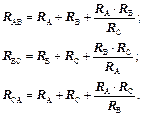
Відзначимо, що ці перетворення можуть бути застосовані тільки в тих випадках, коли в трикутнику опорів або зірці відсутні джерела енергії.

Використання наведених формул перетворення в розрахунках електричних кіл розглянемо на прикладі схеми, відомої під назвою міст Уітстона.

Задача: визначити струм в перемичці ВС наведеної схеми.

Вихідні дані:

Е = 32 В; R ₀ = 1 Ом; R ₁ = 10 Ом; R ₂ = 15 Ом; R ₃ = 25 Ом; R ₄ = 12,5 Ом; R ₅ = 25 Ом.

Розрахунок:

Замінимо трикутник опорів R ₁, R ₂, R ₃ еквівалентною зіркою з променями:

Загальний опір кола:

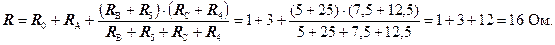
Струм в нерозгалуженій частині кола:

Струми в паралельних вітках (R _B + R ₅) – I_{R 5} і (R _C + R ₄) – I_{R 4}:

.

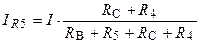Ця формула походить з пропорції 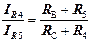(струми в паралельних вітках зворотно пропорційні опорам віток) або .

З математики відома властивість пропорцій: якщо справедлива пропорція , то справедливий вираз , а в цьому випадку – . Так як I _R4 + I _R5 = І, то .

Отже , а I _R4 = І – I _R5 = 2 – 0,8 = 1,2 А.

З рівняння, складеного за другим законом Кірхгофа для контуру BDCB: I _BC R ₃ + I _R5 R ₅ – I _R4 R ₄ = 0, маємо:

.

Лекція 3. Методи розрахунку складних електричних кіл.

План

· Розрахунок складних кіл постійного струму.

q Безпосереднє використання законів Кірхгофа.

q Метод накладання.

q Метод контурних струмів.

q Метод вузлових напруг.

q Метод еквівалентного генератора.

q Активний і пасивний двополюсник.

Розрахунок складних кіл постійного струму.

Використання законів Кірхгофа для розрахунку складних кіл.

Універсальним методом розрахунку складних кіл є метод безпосереднього використання першого закону Кірхгофа для вузлових точок і другого закону Кірхгофа для замкнутих контурів схеми.

Всі ЕРС, струми і опори будь-якої вітки пов’язані між собою рівняннями, що визначаються законами Кірхгофа. Цей зв’язок враховує не тільки величини ЕРС і струмів, а і їх напрямки.

Якщо відомими є величини ЕРС і їх напрямки, а також опори складного кола, то застосовуючи закони Кірхгофа можна скласти стільки незалежних рівнянь, скільки невідомих струмів в цьому колі. Ці рівняння утворюють систему лінійних алгебраїчних рівнянь, розв’язавши яку можна отримати значення невідомих струмів.

Для складання рівнянь необхідно попередньо позначити на схемі довільно обрані додатні напрямки невідомих струмів. Якщо в результаті розв’язання складеної системи рівнянь знайдена величина струму має знак “+”, то це означає, що його фактичний напрямок співпадає з довільно обраним. В протилежному випадку фактичний напрямок струму протилежний обраному напрямку.

Розрахунок складного кола через рівняння Кірхгофа виконується в такій послідовності:

§ при можливості спрощують розрахункову схему (наприклад, можна замінити кілька паралельно з'єднаних опорів одним еквівалентним опором);

§ позначають на схемі відомі напрямки ЕРС;

§ позначаються довільно обрані напрямки струмів;

§ складають рівняння за першим законом Кірхгофа для всіх вузлових точок, крім однієї. Якщо схема містить n вузлів, то незалежних рівнянь можна скласти тільки для (n – 1) вузлів. Рівняння, складене для останнього n– го вузла, буде комбінацією вже складених рівнянь (тобто лінійно залежним) і не дозволить отримати рішення, так як система, що містить залежні рівняння, має нескінченну кількість рішень;

§ складають рівняння, яких за кількістю бракує, за другим законом Кірхгофа (відомо, що для розв’язання системи необхідно, щоб кількість незалежних рівнянь дорівнювало кількості невідомих в даному випадку струмів);

§ розв’язують складену систему рівнянь і визначають невідомі струми. Якщо значення деяких струмів від’ємні, то це означає, що їх фактичний напрямок протилежний умовно прийнятому для них напрямку на початку розрахунку.

Приклад. Визначити розподіл струмів в схемі:

Вихідні дані:

E ₁ = 72 В; E 2 = 43 В; R ₁ = 3 Ом; R ₂ = 4 Ом; R ₃ = 6 Ом; _{R 4} = 10 Ом; R ₅ = 15 Ом.

Попередньо спрощуємо схему і знайдемо опір, еквівалентний опорам R ₃; R ₄; R ₅:

.

Отримаємо спрощену схему, на якій довільно відмічаємо позитивні напрямки невідомих струмів І ₁, І ₂, І ₃.

Схема має два вузли А та В і два контури. Застосовуючи до вузла А і до двох контурів закони Кірхгофа складаємо три рівняння.

.

Розв’язуємо систему рівнянь:

І ₃ = 6 – 1,5 = 4,5 А.

Отже: І ₁ = 6 А; І ₂ = –1,5 А; І ₃ = 4,5 А.

Отриманий від’ємний знак у величині струму І ₂ = –1,5 А означає, що в дійсності цей струм направлений в бік, протилежний напрямку стрілки, що позначає на схемі струм І ₂.

Струм І ₃ розподіляється між паралельними вітками R ₄і R ₅ зворотно пропорційно їх опорам

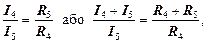звідки

Метод суперпозиції.

Метод суперпозиції (накладання) оснований на принципі незалежності дії ЕРС. Відповідно з цим принципом струм в будь–якій вітці кола з постійними опорами можна уявити як суму часткових струмів, створених в цій вітці кожною з ЕРС окремо.

Розрахунок складного кола за цим методом виконується, поклавши всі ЕРС, крім однієї, рівними нулю. При цьому зберігають незмінними всі опори кола (включаючи опори джерел живлення, ЕРС яких покладені рівними нулю). Для отриманої схеми вже простого кола визначаються струми в усіх вітках.

Такий розрахунок виконується стільки разів, скільки ЕРС діє в колі, що досліджується. Реальний струм в кожній вітці визначається як алгебраїчна сума знайдених часткових струмів.

Відзначимо, що метод суперпозиції можна застосовувати тільки для електричних кіл, в яких опори не залежать від струмів, що по них протікають (такі опори називаються лінійними).

Метод контурних струмів.

При розрахунку складних кіл, що складаються з великої кількості вузлів, переважним є метод контурних струмів, який дозволяє скоротити загальну кількість рівнянь в системі.

Сутність методу розглянемо на схемі складного кола з вузлами A, B, C, D.

Ця схема включає три контури ABCA (І), ADBA (ІІ), CBDC (ІІІ). Кожному контуру умовно приписують довільно направлений контурний струм, однаковий для всіх ділянок цього контуру І _І, І _ІІ, І _ІІІ. У вітках, які є спільними для двох суміжних контурів, фактичний струм дорівнює алгебраїчній сумі двох контурних струмів. Тут:

у вітці АВ протікає струм І ₂ = І _ІІ – І _І,

у вітці ВС – струм І ₅ = І _І – І _ІІІ,

у вітці DB – І ₄ = І _ІІ – І _ІІІ.

Застосовуючи до кожного з контурів другий закон Кірхгофа, отримаємо систему з кількістю рівнянь, рівною кількості невідомих контурних струмів:

Розв’язавши систему і визначивши контурні струми І _І, І _ІІ, І _ІІІ, неважко знайти струми у вітках схеми: І ₁ = І _І, І ₂ = І _ІІ – І _І, І ₃ = І _ІІ, І ₄ = І _ІІ – І _ІІІ, І ₅ = І _І – І _ІІІ, І ₆ = І _ІІІ.

Зауважимо, що при безпосередньому використанні законів Кірхгофа для розрахунку цієї схеми необхідно було б розв’язати систему з шести рівнянь.

Метод вузлових напруг.

Коли електричне коло складається з великої кількості контурів при невеликій кількості вузлів, її розрахунок і аналіз доцільно здійснювати методом вузлових напруг (або метод вузлових потенціалів).

Якщо кількість вузлів в схемі n, то кількість рівнянь, необхідних для розрахунку такого кола дорівнює (n – 1). Невідомими величинами в цих рівняннях є так звані вузлові напруги. У відповідності з цим методом потенціал в одному з вузлів схеми приймають рівним нулю. Інші вузли схеми будуть мати відносно вузла із нульовим потенціалом вузлові напруги U ₁, U ₂, …, U _{n – 1}.

Струм в кожній вітці схеми визначається напругами, прикладеними до вузлів вітки (вузловими напругами), ЕРС, якщо вітка їх містить і опором вітки.

Далі, використовуючи вирази для струмів, складають рівняння за першим законом Кірхгофа для кожного вузла схеми за виключенням вузла з нульовою напругою. Сукупність таких рівнянь утворює систему рівнянь відносно невідомих вузлових напруг.

При складанні рівняння для будь–якого і –го вузла можна скористатись вже готовою універсальною формулою:

,

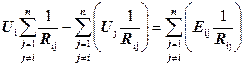за якою:

§ добуток вузлової напруги в і –тому вузлі на суму провідностей віток між і –тим і кожним з сусідніх з і –тим вузлами,

§ мінус сума добутків вузлових напруг в кожному сусідньому з і –тим вузлі на провідність вітки між цим вузлом і і –тим,

§ дорівнює сумі добутків ЕРС у вітці між і– тим і кожним сусіднім з і –тим вузлі (якщо вона є у цій вітці) на провідність цієї вітки.

Складові Е _ij беруться із знаком “+”, якщо ЕРС направлена до і –го вузла і із знаком “–”, якщо вона направлена від і –го вузла.

Розв’язавши систему відносно U _і, можна визначити струми у вітках.

Розглянемо розрахунок електричного кола за цим методом на прикладі такої схеми:

Довільно пронумеруємо вузли схеми, починаючи з нуля. Потенціал у вузлі № 0 приймаємо рівним нулю. Використовуючи наведену формулу, складаємо рівняння для інших вузлів:

§ для вузла № 1:

§ для вузла № 2:

§ для вузла № 3: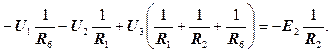

Після розв’язання системи рівнянь відносно невідомих U ₁, U ₂, U ₃, тобто визначення їх значень, розраховуємо струми у вітках. Для цього розглянемо кожну вітку окремо.

§ Вітка з вузлами 0 – 1.

Дія прикладеної до вузлів напруги U ₁ рівноцінна дії включеної ЕРС Е = U ₁. Для такого штучно утвореного контуру складається рівняння за другим законом Кірхгофа IR ₄ = U ₁. З якого: I = U ₁/ R ₄.

Аналогічно для інших віток.

§ Вітка з вузлами 0 – 2.

IR ₅ = U ₂ Þ I = U ₂ / R ₅.

§ Вітка з вузлами 0 – 3.

IR ₂ = Е ₂ + U ₃ Þ I = (Е ₂ + U ₃) / R ₅.

§ Вітка з вузлами 1 – 2.

IR ₃ = – Е ₃ – Е ₁ – U ₂ + U ₁ Þ I = (– Е ₃ – Е ₁ – U ₂ + U ₁) / R ₃.

§ Вітка з вузлами 2 – 3.

IR ₁ = – U ₂ + U ₃ Þ I = (– U ₂ + U ₃) / R ₁.

§ Вітка з вузлами 1 – 3.

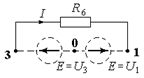
IR ₆ = – U ₁ + U ₃ Þ I = (– U ₁ + U ₃) / R ₆.

Зауваження щодо аналогій з фізичними системами іншої природи.

Рівняння законів Кірхгофа є окремим випадком загального підходу до аналізу фізичних систем різноманітної природи. Цей підхід обумовлений наявністю аналогій між різнорідними фізичними системами – механічними, гідравлічними, пневматичними, тепловими, електричними. Так аналогом електричної напруги є тиск, температура, швидкість; аналогом електричного струму – механічні сили і потоки рідини, газу, теплоти. Подібні аналогії давно помічені і широко використовуються для аналізу об’єктів. На принципі аналогій основана дія аналогових обчислювальних машин (АОМ).

Аналогом першого закону Кірхгофа є рівняння рівноваги – рівняння потоків у вузлах з’єднання елементів. Аналогом другого закону Кірхгофа є рівняння сумісності – рівняння сумісності тисків, температур або швидкостей (переміщень) в будь–якому замкнутому контурі. Наприклад, для пружної механічної системи рівняння рівноваги повинні бути записані для проекцій сил на кожну координатну вісь і для обертальних моментів відносно кожної координатної осі, а рівняння сумісності деформацій виражають цілісність конструкції і уявляють собою рівність нулю сумарної деформації елементів вздовж будь–якого замкнутого контуру; для пневматичної і гідравлічної системи рівняння рівноваги – сума потоків в будь–якому вузлі системи дорівнює нулю, а рівняння сумісності – сума тисків вздовж будь–якого контуру дорівнює нулю; для теплової системи – сума теплових потоків у вузлі і сума температур вздовж контуру дорівнює нулю.

Встановлення аналогій обумовлює можливість викладання питань моделювання різних технічних об’єктів з єдиних позицій і дозволяє одні і ті ж математичні методи застосовувати для розв’язання задач з різним фізичним змістом (в різних галузях техніки розроблені методи, що мають хоч і різні назви, але однакову сутність).

Наприклад, метод вузлових напруг та метод контурних струмів для моделювання електричних систем і метод переміщень та метод сил в будівельній механіці.

Метод вузлових напруг і метод переміщень з формальної точки зору уявляють собою один і той же метод, який називають вузловим методом. Дійсно, і метод вузлових напруг, і метод переміщень ґрунтуються на використанні рівняння рівноваги; як основні величини, що характеризують стан об’єкту, вибрані змінні, що відносяться до вузлів еквівалентної схеми. Вузловий метод успішно використовується для моделювання гідравлічних систем і вважається одним з найбільш ефективним для отримання математичних моделей.

Контурний метод в теорії електричних кіл відомий як метод контурних струмів, а в будівельній механіці – як метод сил. Цей метод також використовується для отримання математичних моделей у вигляді системи алгебро–диференціальних рівнянь.

Метод еквівалентного генератора.

На практиці часто буває необхідним знайти величину струму тільки в одній з віток складного кола. В таких випадках найбільш ефективним є метод еквівалентного генератора.

Суть методу полягає в тому, що будь–яке складне коло уявляється еквівалентною схемою у вигляді активного двополюсника – одна ЕРС E і один резистор з опором R. Параметри цього активного двополюсника E і R визначаються в режимі холостого ходу, тобто при відключенні від клем реального кола вітки, в якій необхідно знайти струм. ЕРС Е активного двополюсника дорівнює напрузі холостого ходу на клемах реального кола, до яких повинна бути приєднана вітка, а значення внутрішнього опору R дорівнює опору кола між цими клемами при умові, що всі ЕРС в реальному колі дорівнюють нулю.

Оскільки активний двополюсник по суті є джерелом ЕРС, тобто генератором, то звідси і витікає відповідна назва методу.

На малюнку показане складне електричне активне (тобто містить джерела електроенергії) коло з винесеною віткою ab, в якій визначається струм, і поруч її еквівалентна схема.

Струм у вітці ab: I _н = Е / (R + R _н).

Напруга U _{х. х} = Е еквівалентної схеми генератора визначається розрахунком кола при відключеному навантаженні R _н будь–яким з відомих методів розрахунку складних кіл або експериментально.