 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Состав и характеристики атомных ядер
|
|
Ядро любого атома, кроме атома легкого водорода, состоит из частиц – нуклонов двух типов: Z протонов и N нейтронов. Нейтрон был открыт в 1932 г. Джеймсом Чэдвиком, тогда же Карлом Андерсоном – позитрон. Ядро атома легкого водорода состоит из одного протона.
Протон открыт в является заряженной частицей – qp = +e. Масса протона составляет mp = 1.67265 10–27 кг. В ядерной физике принято энергию частиц выражать в единицах энергии (эВ), для чего умножают массу на квадрат скорости света c2, тогда масса протона mp = 938.26 МэВ. Протон имеет спин, равный s = 1/2.
Нейтрон также имеет спин s = 1/2. Его масса близка к массе протона и составляет mn =1.67495 10–27 кг или в единицах энергии (эВ) mp = 939.55 МэВ. Однако нейтрон не имеет электрического заряда. В свободном состоянии нейтрон является радиоактивным, он самопроизвольно распадается, превращаясь в протон. При этом выделяется антинейтрино.
 (13.1)
(13.1)
В составе ядра нейтрон стабилен.
Атом характеризуют зарядовым числом Z (которое равно числу протонов в ядре). Число Z определяет порядковый номер атома в таблице Менделеева. Массовое число A = N + Z показывает полное число нуклонов в ядре. Масса всех нуклонов A вносит основной вклад в массу всего атома. Ядро также называют нуклидом. Принятая схема нуклида имеет вид:  Кроме нуклонов других частиц в ядре нет. Однако нуклоны не являются элементарными частицами: каждый из них состоит из трех кварков, о которых речь пойдет в другой лекции.
Кроме нуклонов других частиц в ядре нет. Однако нуклоны не являются элементарными частицами: каждый из них состоит из трех кварков, о которых речь пойдет в другой лекции.
Атомы, ядра которых имеют одинаковые зарядовые числа Z и различные массовые числа A, имеют одни и те же химические свойства и называются изотопами. Изотопы одного и того же химического элемента различаются друг от друга лишь по числу нейтронов в ядре. Большинство веществ с атомами одного и того же Z представляют смесь различных изотопов. Так, водород, углерод и кислород имеют по 3 изотопа:  – обычный водород,
– обычный водород,  – дейтерий,
– дейтерий, 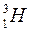 – тритий;
– тритий;  ;
;  ; у олова существует 10 изотопов.
; у олова существует 10 изотопов.
Атомы, ядра которых имеют одни и те же массовые числа A, называются изобарами. Изобары, т.е. ядра с различными Z, соответствуют ядрам атомов различных химических элементов.
В опытах Резерфорда по рассеянию α -частиц на атомах вещества было установлено, что ядра имеют конечный размер. С этого момента прошло много времени, однако до сих пор наиболее предпочтительными при определении размера ядра являются опыты по рассеянию частиц на атомных ядрах. Поскольку электроны испытывают только электростатическое взаимодействие с ядрами, то распределение заряда внутри ядра изучают с помощью рассеяния электронов. О распределении ядерной материи внутри ядра судят по рассеянию нейтронов, так как в этом случае взаимодействие между частицами сводится только к специфическому ядерному. Для того, чтобы ядро «почувствовало» налетающую частицу, учитывая массы, энергия электрона должна составлять не меньше 124 МэВ, а энергия нейтрона не меньше 8 МэВ. Эксперименты с электронами и нейтронами различных (но удовлетворяющих указанным условиям) энергий показали, что объем ядра пропорционален числу нуклонов в его составе:
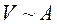 (13.2)
(13.2)
В ядрах со спином, большим или равным 1, действительно наблюдается отклонение от сферической формы. Такие ядра могут быть сжатыми или вытянутыми эллипсоидами вращения, при этом разница между их большой и малой осями никогда не превышает 20% и, как правило, существенно меньше. В первом приближении ядро можно считать шаром, радиус ядра таким образом:  (13.3)
(13.3)
Константа R0 ≈ 1.3·10–15м. Ее приблизительное значение связано с тем, что величина радиуса ядра, полученная по распределению ядерной материи, отличается от значения радиуса, полученного по распределению заряда. Это означает, что заряд и вещество распределены внутри ядра различным способом.
В рамках ядерной теории используют величину 1 ферми = 1 f = 10–15м.
Тогда радиус ядра равен  .
.
Спином ядра I называется полный угловой момент ядра. Для ядра с массовым числом A он равен:  (13.4)
(13.4)
В этом выражении первый член справа равен суммарному спиновому моменту нуклонов, а второй – суммарному орбитальному моменту нуклонов в ядре. Значения Si и li определяются значениями соответствующих квантовых чисел: sp = sn = 1/2 и l = 0, 1, 2,...
Магнитный момент ядра μя складывается из собственных магнитных моментов протонов и нейтронов и орбитальных магнитных моментов протонов (нейтрон обладает нулевым орбитальным магнитным моментом при любом l).
Итак, в состав ядра входят A нуклонов. Однако не все сочетания протонов и нейтронов образуют стабильные ядра. Это связано с существованием ядерных уровней энергии. Поскольку и протоны, и нейтроны являются фермионами (их спин s = 1/2), то на каждом уровне может быть не больше двух протонов и двух нейтронов. Заполнение уровней идет по принципу минимизации системы объединившихся частиц. Например, рассмотрим два изотопа  и
и 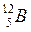 . Первые два уровня у них (рис. 13.1) заполнены одинаково.
. Первые два уровня у них (рис. 13.1) заполнены одинаково.

Рис. 13.1 Стабильный изотоп углерода и нестабильный изотоп бора
На последнем уровне в нуклиде 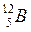 расположен 12-ый нейтрон, в тоже время на предыдущем уровне до полного заполнения не хватает протона. Энергия системы из трех нейтронов и одного протона будет больше чем энергия системы двух протонов и двух нейтронов. Поэтому, изотоп
расположен 12-ый нейтрон, в тоже время на предыдущем уровне до полного заполнения не хватает протона. Энергия системы из трех нейтронов и одного протона будет больше чем энергия системы двух протонов и двух нейтронов. Поэтому, изотоп  не будет стабильным и довольно быстро распадется. В тоже время изотоп
не будет стабильным и довольно быстро распадется. В тоже время изотоп  (содержащий 5 протонов и 6 нейтронов) является стабильным.
(содержащий 5 протонов и 6 нейтронов) является стабильным.
В легких ядрах (A < 20), как правило, число протонов и нейтронов одинаково (или отличается не единицу в случае ядер с нечетным числом нуклонов, причем число нейтронов обязательно больше числа протонов). В тяжелых ядрах доля нейтронов становится все больше. В таких ядрах помимо принципа минимизации энергии оказывается существенным кулоновское отталкивание протонов. В ядрах с числом протонов больше 10 это отталкивание настолько велико, что для устойчивости ядра эту силу необходимо чем-либо компенсировать. Между нейтронами действуют только ядерные силы притяжения. Поэтому увеличение числа нейтронов в составе ядра приводит к уравновешиванию сил, т.е. к стабильности ядра.
13.2. Модели ядра: капельная и оболочечная
Для объяснения свойств ядер, процессов происходящих с их участием, а также для предсказания возможных новых эффектов, требуется построение такой теории ядра, которая корректно и полно описывала бы все ядерные явления. Это весьма сложная задача, поскольку специфика ядра не позволяет простыми путями получать информацию о внутренних процессах и строении. Кроме того, ядро является системой большого числа частиц. Математическая задача уже в случае 3 – 4 взаимодействующих тел становится решаемой только с помощью высокопроизводительной вычислительной техники. Построение качественных моделей – это обходной путь, позволяющий сравнительно простыми математическими законами описать совокупность свойств ядер.
Одна из таких моделей – капельная модель – была предложена Я. И. Френкелем в 1939 г. и затем развита Н. Бором. Френкель обратил внимание на то, что нуклоны в ядре, так же как молекулы в капле жидкости, взаимодействуют с ограниченным числом близлежащих частиц. Крайне малая сжимаемость ядерного вещества дополнила аналогию с жидкостью. Учитывая, что в ядре содержится некоторое количество положительно заряженных протонов, то в рамках данной модели следует считать ядро наэлектризованной каплей.

Рис. 13.2. Капельная модель ядра
Капельная модель позволяет вывести полуэмпирическую формулу для энергии связи в ядре. Системе нуклонов предпочтительнее состояние с максимальным значением энергии связи. При этом существует ряд сил, наличие которых снижает значение полной энергии.
Для определения зависимости удельной энергии связи ядра от числа нуклонов необходимо ввести энергию U, которая характеризует каждую нуклон-нуклонную связь. На каждый из пары нуклонов приходится половина этой энергии. Из геометрических соображений следует, что каждый нуклон окружен 12 нуклонами ближнего порядка. Тогда объемная энергия ядра равна:  (13.5)
(13.5)
где A число нуклонов в ядре, положим произведение 6U = а.
В действительности в каждом ядре часть нуклонов находится на поверхности ядра и имеет менее 12 «соседей». Поэтому необходимо учитывать поверхностную энергию. Она играет заметную роль в легких ядрах, в которых большая часть нуклонов находится на поверхности.
Учитывая формулу (13.3), получим, что площадь поверхности ядра равна:  (13.6)
(13.6)
Поверхностная энергия отрицательна и пропорциональна площади поверхности ядра, следовательно:
 (13.7)
(13.7)
Существование поверхностной энергии определяет стремление ядра принять сферическую форму, которая обеспечивает минимальную площадь поверхности и, следовательно, минимальное значение поверхностной энергии при заданном объеме (количестве нуклонов). Т.о., сферическая форма соответствует минимальному снижению полной энергии связи ядра. Аналогичным образом силы поверхностного натяжения заставляют каплю жидкости принимать вид сферы, если на нее не действуют внешние силы.
Электростатические силы отталкивания между каждой парой протонов в ядре определяют еще одну поправку к полной энергии связи ядра. Она эквивалентна работе, которую нужно совершить, чтобы свести вместе из бесконечности Z протонов в объем, равный объему ядра. В ядре, содержащем Z протонов, эта работа пропорциональна числу протонных пар 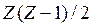 и обратно пропорциональна радиусу ядра (13.3):
и обратно пропорциональна радиусу ядра (13.3):
 (13.8)
(13.8)
Кулоновская энергия также отрицательна, поскольку обусловлена отталкиванием нуклонов, т.е. направлена на разрушение связей в ядре.
Полная энергия связи ядра Eсв является суммой объемной, поверхностной и кулоновской энергий:
 (13.9)
(13.9)
Откуда удельная энергия связи ядра, т.е. энергия, приходящаяся на один нуклон, равна:
 (13.10)
(13.10)
На рис. 13.3 показаны экспериментальные зависимости разных видов энергий от числа нуклонов в ядре.
Сравнивая соответствующие кривые с теоретическими зависимостями, полученными в рамках капельной модели ядра, можно сказать, что данная теория вполне может быть использована в теоретических расчетах некоторых параметров ядра и для объяснения ряда эффектов.

13.3. Зависимость удельной энергии связи атомного ядра от числа нуклонов
Оболочечная модель была развита лауреатами Нобелевской премии американкой Марией Гепперт-Майер и немцем Йоханом Х. Д. Йенсеном.
Согласно этой модели, нуклоны в ядре взаимодействуют не друг с другом (как это предполагается в капельной модели), а с усредненным центрально-симметричным силовым полем. Аналогичная ситуация реализуется в многоэлектронном атоме, где движение каждого электрона происходит в усредненном поле ядра и остальных электронов. В рамках модели нуклоны находятся на некоторых энергетических уровнях, сгруппированных в оболочки. Нуклоны, так же как и электроны, являются ферми-частицами, то есть на каждом уровне могут находиться два нуклона с антипараллельными спинами.
С увеличением числа нуклонов в ядре происходит постепенное заполнение оболочек, при этом некоторые свойства ядер периодически повторяются в зависимости от Z (число протонов) и N (число нейтронов), так же как периодически меняются свойства атомов в зависимости от Z. Напомним, что в атомах с 2, 10, 18, 36, 54 и 86 электронами все оболочки полностью укомплектованы (см. раздел 8). Такие атомы являются инертными газами, причем электронные конфигурации довольно устойчивы, что объясняет их химическую инертность.
В ядрах ситуация такова: ядра с числом нейтронов или протонов, равным 2, 8, 20, 28, 50, 82 и 126, имеют бóльшую распространенность. Эти числа называются магическими. Логично предположить, что ядра с магическим числом протонов или нейтронов более стабильны – такие ядра также называют магическими. Ядра, в которых число и протонов, и нейтронов является магическим, называются дважды магическими. Они особенно устойчивы. Существует всего пять подобных ядер:
 (Z = 2, N = 2)
(Z = 2, N = 2)
 (Z = 8, N = 8)
(Z = 8, N = 8)
 (Z = 20, N = 20)
(Z = 20, N = 20)
 (Z = 20, N = 28)
(Z = 20, N = 28)
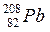 (Z = 82, N = 126)
(Z = 82, N = 126)
В частности, ядро гелия является настолько стабильным, что способно как единое целое испускаться тяжелыми ядрами при радиоактивном распаде (см. далее раздел 14). Ядро гелия называется α -частицей.
Поскольку заполнение энергетических состояний ядра происходит по принцип Паули (см. раздел 8), то логичным будет предположить, что ядра, содержащие четное число протонов и нейтронов («четно-четные» ядра), т.е., имеющие заполненные уровни обоих типов, будут более стабильными, чем «нечетно-нечетные» ядра, уровни протонного и нейтронного типов которых являются заполненными наполовину. Это подтверждается фактом существования 160 стабильных «четно-нечетных» нуклидов, тогда как среди «нечетно-нечетных» нуклидов стабильны только четыре:  ,
,  ,
,  и
и  .
.
Согласно оболочечной модели ядра, как и атомы, могут иметь возбужденные состояния. Переход в одно из таких состояний возможен под действием внешней энергии. Соответственно снятие возбуждения происходит с излучением такой же энергии. В отличие от атомов, энергии, характерные для ядерных переходов, имеют величину порядка нескольких МэВ (1 МэВ = 106 эВ). Описание энергетических переходов в ядре с помощью оболочечной модели хорошо согласуется с экспериментальными данными.
Таким образом, рассмотренные модели с одной стороны можно считать близкими к верным, т.к. подтверждаются экспериментально. С другой стороны, они противоречат друг другу. В рамках капельной модели нуклоны считаются взаимодействующими (сталкивающимися) между собой, в рамках оболочечной модели нуклоны движутся в силовом поле независимо друг от друга. Даже в плотноупакованном ядре нуклон-нуклонные столкновения отсутствуют из-за принципа запрета Паули. При столкновении один нуклон должен передать свою энергию другому нуклону, переходя в состояние с меньшей энергией, при этом второй нуклон переходит в состояние с большей энергией. Однако все состояния с низкой энергией уже заняты, и такая передача энергии может происходить только при нарушении принципа Паули, т.е. не может произойти.
Несмотря на очень разный подход и модель жидкой капли, и оболочечная модель ядра позволяют объяснить большое количество свойств ядер. В последнее время делались успешные попытки создания теорий, обладающих достоинствами каждой из этих моделей. Одной из самых удачных является обобщенная модель, совмещающая принципы капельной и оболочечной моделей.
Дата публикования: 2014-11-04; Прочитано: 1219 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
