 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Собственная проводимость
|
|
Рассмотрим квантовую теорию проводимости различных веществ. Напомним, что проводимостью называется способность носителей заряда осуществлять направленное движение согласно приложенному электрическому полю (носителей отрицательного заряда против поля, положительного заряда – по полю). В случае полупроводниковых веществ возможны два типа проводимости в зависимости от чистоты химического состава вещества.
Различают собственные и примесные полупроводники. К числу собственных относятся химически чистые полупроводники, то есть такие полупроводники, в состав которых входят атомы (или молекулы) только одного вида и отсутствуют посторонние включения. В таких полупроводниках наблюдают только собственную проводимость.
Собственная проводимость возникает при переходе электронов с верхних уровней валентной зоны в зону проводимости в случае получения им дополнительной достаточной энергии, которая равна (или несколько больше) ширине запрещенной зоны Eg. Данную энергию, как уже говорилось в лекции 9, электрон может получить в результате тепловых колебаний решетки или под действием кванта света hν.

Рис. 12.1. Собственная проводимость полупроводника
Так как энергия тепловых колебаний, как правило, значительно меньше энергии кванта света, то какая именно энергия спровоцирует появление проводимости, зависит от ширины запрещенной зоны кристалла. Переход электрона в зону проводимости соответствует рождению двух свободных частиц: электрона, энергия которого оказывается равной одному из разрешенных значений из зоны проводимости, а также дырки, энергия которой равна одному из значений валентной зоны. Эти частицы являются носителями тока, причем вклад в проводимость вносят как электроны, так и дырки. Если приложить разность потенциалов к такому кристаллу, и электроны и дырки смогут двигаться вдоль всего образца. Это явление уже рассмотрено во второй лекции, оно называется внутренним фотоэффектом.
Можно найти электропроводность данного вещества. Для этого воспользуемся распределением электронов и дырок по энергиям (см. раздел 10). Так как электроны и дырки являются фермионами, т.е. частицами с полуцелым спином, это означает, что они подчиняются статистике Ферми-Дирака:
 (12.1)
(12.1)
Параметр EF носит название энергии Ферми. Уровень Ферми – это виртуальный уровень, который соответствует середине между всеми занятыми и всеми свободными состояниями при условии, что тех и других имеется одинаковое количество. В идеале все свободные уровни располагаются выше уровня Ферми, все занятые – ниже. Однако в реальных кристаллах свободный уровень может оказаться ниже уровня Ферми, если выше уровня Ферми найдется занятый электроном уровень. Для металлов уровень Ферми находится в зоне проводимости. Для собственных (т.е. чистых) полупроводников энергия Ферми при комнатной температуре соответствует приблизительно середине запрещенной зоны, следовательно:
 (12.2)
(12.2)
где Eg – ширина запрещенной зоны.
Количество электронов, перешедших в зону проводимости (равно как и дырок, оставшихся в валентной зоне), будет пропорционально вероятности того, что электрон обладает соответствующей энергией:
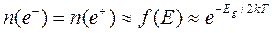 (12.3)
(12.3)
Проводимость, очевидно, зависит от числа свободных носителей тока, то есть оказывается также пропорциональна функции f(E):
 (12.4)
(12.4)
или  (12.5)
(12.5)
Видно, что электропроводность собственных полупроводников экспоненциально растет с температурой (рис. 12.2). Измерив электропроводность полупроводника при различных температурах, можно определить ширину запрещенной зоны. В полулогарифмических координатах (как на рис. 12.2) тангенс угла наклона прямой будет пропорционален Eg.
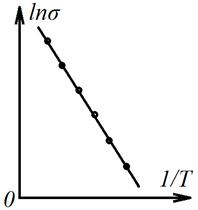
Рис. 12.2. Зависимость электропроводности
собственного полупроводника от температуры
Напомним, что электропроводность металлов линейно уменьшается с ростом температуры. Такое отличие объясняется тем, что природа проводимости в полупроводниках и металлах принципиально различна.
Дата публикования: 2014-11-04; Прочитано: 744 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
