 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Квантовая теория проводимости металлов
|
|
Рассмотрим процесс проводимости с квантовой точки зрения. В предыдущей лекции было сказано, что при объединении атомов в кристаллическую решетку происходит снижение высоты стенок потенциального барьера вокруг ядра каждого атома. При этом внешние (валентные электроны) получают возможность при определенных условиях перемещаться по всему кристаллу, электроны же внутренних оболочек остаются на своих местах. Для металлической решетки условием освобождения электронов является воздействие на кристалл энергии порядка 10–22 эВ, т.е. энергии теплового движения при любой температуре достаточно, чтобы электрон оторвался от ядра и стал свободным. Таким образом, в отличие от полупроводников, металлы всегда имеют электроны проводимости. Поэтому при рассмотрении процесса проводимости изучают не факторы, влияющие на образование свободных электронов, а наоборот – факторы, мешающие проводимости. Напомним, что в направленном движении зарядов в металлах могут участвовать только электроны (понятие дырка здесь не возникает).
Отличие механизмов проводимости в металлах и полупроводниках, объясняет обратную (по отношению к случаю полупроводников) зависимость электропроводности от температуры (рис. 12.8). В металлах наблюдается уменьшение проводимости с ростом температуры. Это связано с одним из факторов, определяющих проводимость металла – усилением тепловых колебаний кристаллической решетки, что сопровождается увеличением числа столкновений свободных электронов с положительными ионами решетки – увеличением сопротивления.

Рис. 12.8. Зависимость удельного сопротивления металлов от температуры
При понижении температуры число столкновений электронов с атомами решетки снижается и при 0 K обращается в нуль. Сопротивление металла также зависит от того, насколько идеальной является кристаллическая решетка. Реальные кристаллы имеют довольно много разнообразных дефектов. Искажение строго периодичной структуры может быть обусловлено заменой атомов решетки инородными атомами, появлением атомов в междоузлиях, наконец, отсутствием каких-либо атомов решетки (вакансии). Любой из этих дефектов может оказывать влияние на движение электрона в кристалле, причем при небольшой концентрации дефектов от температуры это влияние не зависит. При температуре 0 K, когда колебания решетки отсутствуют, остаточное сопротивление металлов, не переходящих в сверхпроводящее состояние (рис. 12.8 кривая 1), будет обусловлено дефектностью кристаллической решетки.
Если в единице объема металла имеется n свободных электронов. Дрейфовой скоростью электронов называют среднюю скорость перемещения электрона в пределах кристалла:  (12.8)
(12.8)
В отсутствие внешнего поля дрейфовая скорость равна нулю и электрический ток в металле отсутствует. При наложении на металл внешнего электрического поля напряженностью 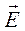 дрейфовая скорость уже не будет равна нулю, согласно закону Ома (см. раздел «электромагнетизм» тему «постоянный ток») дрейфовая скорость электронов конечна и пропорциональна силе
дрейфовая скорость уже не будет равна нулю, согласно закону Ома (см. раздел «электромагнетизм» тему «постоянный ток») дрейфовая скорость электронов конечна и пропорциональна силе  , действующей на электрон, заряд которого равен
, действующей на электрон, заряд которого равен  . Согласно закону Ньютона, силе должно быть пропорционально ускорение, а не скорость. Единственным случаем в механике, когда сила оказывается пропорциональной скорости, является ситуация, когда помимо внешней силы на тело действует еще и сила сопротивления среды. В металле также можно рассмотреть силу сопротивления движению электрона:
. Согласно закону Ньютона, силе должно быть пропорционально ускорение, а не скорость. Единственным случаем в механике, когда сила оказывается пропорциональной скорости, является ситуация, когда помимо внешней силы на тело действует еще и сила сопротивления среды. В металле также можно рассмотреть силу сопротивления движению электрона:
 (12.9)
(12.9)
где  – коэффициент пропорциональности, в данной ситуации
– коэффициент пропорциональности, в данной ситуации  , m* – эффективная масса электрона (см. раздел 11), τ – представляет собой время релаксации, которое характеризует процесс восстановления равновесия между электронами и кристаллической решеткой, которое было нарушено действием внешнего поля
, m* – эффективная масса электрона (см. раздел 11), τ – представляет собой время релаксации, которое характеризует процесс восстановления равновесия между электронами и кристаллической решеткой, которое было нарушено действием внешнего поля  .
.
Тогда уравнение, описывающее поведение электронов в металле будет иметь вид:  (12.10)
(12.10)
Решив это уравнение, можно найти дрейфовую скорость электронов в металле, находящемся во внешнем электрическом поле:
 (12.11)
(12.11)
Тогда плотность тока в металле равна:
 (12.12)
(12.12)
где n – количество свободных электронов в данном объеме, другими словами – концентрация электронов в металле.
Сравнивая полученное выражение с законом Ома в дифференциальной форме:  , получим, что:
, получим, что:  (12.13)
(12.13)
Дата публикования: 2014-11-04; Прочитано: 1741 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
