Функция Кирхгофа. Абсолютно черное тело

Поток энергии, испускаемый единицей поверхности излучающего тела по всем направлениям (в пределах телесного угла 2π), называют энергетической светимостью тела R, которая является функцией температуры тела и частоты излучения. Если поток энергии, исходящий с единичной поверхности тела в интервале частот (ω, ω+dω) составляет dR_ω, то при малом значении dω поток dR_ω пропорционален dω:

(1.1)

Величина r_ω называется испускательной способностью тела и также является зависящей от температуры тела и частоты излучения. Очевидно, что испускательная способность и энергетическая светимость являются взаимосвязанными функциями:

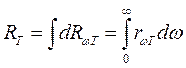(1.2)

Поскольку излучение может быть описано не только частотой ω, но и длиной волны, которая обратно пропорциональна частоте:

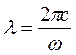(1.3)

то интервалу частотного спектра dω соответствует малый участок dλ по шкале длин волн:

(1.4)

Соответственно интервалу длин волн (λ, λ+dλ) отвечает энергетическая светимость (1.5)

где r_λ – испускательная способность тела в диапазоне длин волн (λ, λ+dλ). Тогда формулу (1.2) нужно переписать в виде:

(1.2')

Таким образом, можно охарактеризовать определенный участок спектра двумя взаимосвязанными интервалами dω и dλ. В этом случае испускательные способности связаны соотношением:

(1.6)

Наряду с этими параметрами рассматривают поглощательную способность тела в интервале частот (ω, ω+dω), которая определяется как отношение потока поглощенной энергии электромагнитного излучения dФ'_ω к потоку падающего излучения dФ_ω.

(1.7)

Поглощательная способность является безразмерной величиной, ее значение не может быть больше единицы.

Учитывая, что температура (следовательно и энергия) тел в термодинамическом равновесии не меняется, то тело, которое больше испускает, вынуждено для поддержания этого равновесия больше поглощать. Математически это можно выразить следующим образом:

(1.8)

где индексы 1, 2, 3 и т.д. относятся к разным телам.

Эту закономерность установил Густав Кирхгоф: отношение испускательной и поглощательной способностей не зависит от природы тела, оно является для всех тел одной и той же универсальной функцией частоты (или длины волны) и температуры:

(1.9)

Эта функция называется функцией Кирхгофа и используется во всех основных теоретических расчетах, касающихся теплового излучения.

Если в формуле (1.9) r_ω заменить на r_λ, то есть воспользоваться описанием излучения с помощью длин волн, то вместо «частотной» функции Кирхгофа f(ω,Т) получим функцию длин волн φ(λ,Т), которой удобно пользоваться при экспериментальных исследованиях.

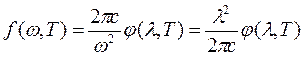(1.10)

Следует заметить, что необходимо понимать различие между испусканием излучения и его отражением. Этот процесс наблюдается наряду с испусканием и поглощением, но на значении функции Кирхгофа (1.9) не сказывается. Падающее на тело излучение распределяется на две части – поток поглощенного и поток отраженного излучений. Поглощенная энергия должна израсходоваться на испускание такого же потока, какой был поглощен. В противном случае излучение не могло бы удовлетворять условию термодинамического равновесия.

Из закона Кирхгофа следует, что при данной температуре максимальной интенсивностью будут обладать лучи тех частот (длин волн), которые тело при той же температуре сильнее всего поглощает.

Тело, которое характеризуется максимально возможной поглощательной способностью а_ωТ = 1, называют абсолютно черным (АЧТ) – оно при любой температуре полностью поглощает всю энергию падающих электромагнитных волн независимо от их частоты, поляризации и направления распространения. Из формулы (1.9) следует, что универсальная функция Кирхгофа f(ω,Т) – это испускательная способность абсолютно черного тела.

Среди реальных тел нет абсолютно черного тела. Однако существуют тела, которые довольно близки по свойствам к абсолютно черному в определенных диапазонах частот. В частности, для наглядной человеку видимой части спектра хорошим приближением являются сажа, платиновая чернь, черный бархат. Эти тела имеют поглощательную способность близкую к единице лишь в ограниченном диапазоне частот, в далекой инфракрасной же области а_ωТ заметно меньше единицы.

Рис.1.2. Модель АЧТ

Для изучения спектра излучения АЧТ при различных температурах используют почти замкнутую полость, снабженную малым отверстием. Опыт показывает, что если размер отверстия меньшего 1/10 диаметра полости, падающее излучение всех частот полностью поглощается. Аналогичную ситуацию мы наблюдаем каждый день: открытые окна домов со стороны улицы кажутся черными, хотя внутри комнат достаточно светло из-за отражения света от стен. Через окно или через отверстие (в рассматриваемой модели – см. рис. 1.2) излучение попадает внутрь полости и, прежде чем выйти из него, претерпевает многократные отражения. Каждое из таких отражений сопровождается поглощением части энергии, в результате чего практически все излучение любой частоты поглощается полостью. Согласно закону Кирхгофа испускательная способность такого устройства очень близка к f(ω,Т) при температуре равной температуре стенок полости. То есть, если температура стенок полости является постоянной, то излучение, выходящее из отверстия, будет достаточно близко к излучению абсолютно черного тела при указанной температуре.

Если это излучение разложить на составляющие, то получится кривая зависимости интенсивности излучения абсолютно черного тела от длины волны, то есть спектр его излучения.

Рис.1.3. Спектр излучения АЧТ

Форма кривой спектра испускательной способности черного тела (рис. 1.3) и положение ее максимума λ_max зависят от температуры тела. Площадь под кривой равна энергетической светимости R_T тела при данной температуре (см. формулу 1.2). Было получено, что спектральная кривая излучения для тела с меньшей температурой укладывается под кривой для тела с большей температурой, то есть при снижении температуры уменьшается поток энергии, испускаемый единицей поверхности тела.