Законы Ома и Джоуля-Ленца в интегральной форме

Законы Ома и Джоуля-Ленца в дифференциальной форме устанавливают соотношения в локальных точках проводника. Однако, используя эти соотношения, можно получить формулы для проводника конечных размеров. Выделим в проводнике цилиндр с площадью основания S и высотой , в пределах которого поле вектора можно считать однородным (рисунок 40).

Применим к такому цилиндру закон Ома в диффе ренциальной форме (13)

Используя связь между напряженностью и потенциалом

2

отсюда , (14)

где U – напряжение между крайними точками цилиндра. Таким образом, в отличие от заряженного проводника поверхность проводника с током не является эквипотенциальной. С учетом (14) преобразуем (13)

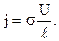
Умножив левую и правую части этого равенства на s и приняв во внимание, что , получим

. (15)

Соотношение (15), устанавливающее прямую пропорциональную зависимость между приложенным к проводнику напряжением и силой тока через него. Называется законом Ома в интегральной форме. Величина называется проводимостью проводника. Обратная ей величина

(16)

называется сопротивлением проводника.

С учетом этого закон Ома для однородного участка цепи часто записывают в виде

. (17)

В электрических цепях однородные проводники применяются в различных комбинациях последовательного и параллельного соединений. Используя закон Ома (17) для однородного участка цепи, нетрудно получить известные из школьного курса формулы для последовательного и параллельного соединений

,

.

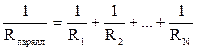Следует иметь в виду, что по формуле (16) находится сопротивление однородного проводника, у которого и S = const. Если, например, удельное сопротивление и площадь поперечного сечения проводника изменяются по его длине, то

.

Удельное сопротивление проводника сложным образом зависит от температуры. Экспериментально установлено. Что в узком температурном диапазоне эта зависимость в первом приближении является линейной ,

где r₀ – удельное сопротивление при 0 ⁰С,

- температурный коэффициент сопротивления проводника.

Применим к изображенному на рисунке 3 цилиндру закон Джоуля-Ленца в дифференциальной форме (11). Который позволяет рассчитать количество теплоты в единице объема за единицу времени при протекании тока. Тогда количество теплоты, выделившееся в объеме цилиндра за время t

. (18)

Выражение (18) представляет закон Джоуля-Ленца в интегральной форме для однородного проводника. Используя закон Ома (17), формуле (18) можно придать другой вид

(19)

Основываясь на выражениях (18) и (19), можно рассчитать тепловую мощность, которая выделяется в цепи при протекании тока