Изосова Л.А., Изосов А.В. 5 страница

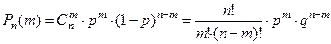. (1)

Полученная формула называется формулой Бернулли.

Пример 1. В среднем пятая часть поступающих в продажу автомобилей некомплектна. Найти вероятность того, что среди 10 – ти прибывших автомобилей имеют некомплектность: а) три автомобиля; б) хотя бы три.

Событие 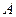- автомобиль имеет некомплектность. Тогда, по условию,

а) По формуле (1),

б) Событие 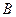- «хотя бы три автомобиля некомплектны», те. от 3 – х до 10 – ти. Его вероятность проще искать через вероятность противоположного событие - «менее 3 – х ав- томобилей некомплектны».

Тогда

Так как события, состоящие в различном числе появлений события 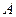в серии из 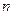независимых испытаний образуют полную группу несовместных событий, то сумма их вероят -ностей равна единице, т.е.

Эта сумма представляет собой разложение 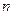- й степени бинома (бином Ньютона) и связанное с ней распределение вероятностей числа появлений события 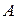в серии из 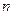опытов называется биномиальным распределением.

Учмтывая это, для вычисления вероятностей возможного числа появлений события 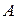в серии из 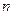независимых ис- пытаний можно ввести так называемую производящую функ- цию:

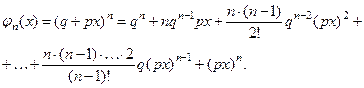
Эта функция обладает тем свойством, что коэффициент, стоя- щий перед в этой сумме равен вероятности .

Пример 2. Предполагается, что в среднем 20% открываю –щихся малых предприятий разоряются в течение года. Найти вероятность того, что после года работы из 6 – ми вновь от - крывшихся предприятий не разорится: а) ровно 5; б) хотя бы четыре.

Вероятность того, что предприятие разорится 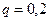, со - ответственно, вероятность того, что оно не разорится, равна Для решения воспользуемся производящей функцией.

Непосредственным сложением можем проверить, что сумма всех коэффициентов в этом разложении равна 1. Тогда, в случае а): , т.е. коэффициент, стоящий перед . В случае б): , т.е. сумма коэффициен- тов, стояший перед .

Аналогичную производящую функцию можно ввести и для случая, когда в серии из 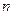испытания вероятности появления события в каждом испытании различны. Пусть вероятность по- явления события в испытании равна и, соот- ветственно, вероятность того, что событие не произошло - . Тогда о вероятностях определённого числа появлений события 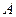в данной серии опытов можно судить по значению коэф -фициентов перед определёнными степенями 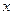в разложении по степеням 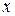следующей производящей функции:

.

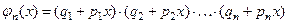Пример 3. Пусть пять баскетболистов бросили по одному разу мяч в корзину. Найти вероятность того, что будет три точных попадания, если для 1 – го и 3 – го вероятности попа -дания равны 0,7, для 2 –го - 0,6, для 4 – го - 0,8 и для 5 – го - 0,9.

В этих условиях, ,

Тогда производящая функция имеет вид:

Сумма коэффициентов в разложении равна единице.

Тогда вероятность того, что будет три попадания мяча в кор- зину равна коэффициенту перед , т.е.

Если бы мы искали эту вероятность, применяя теоремы сло- жения и умножения вероятностей, то вычисления были бы на- много более громоздкими.

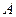Определение. Наивероятнейшим числом появлений со- бытия в серии из 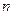независимых испытаний называется число, для которого является наибольшим.

Например, в примере 2, ; в примере 2, .

Используя формулу Бернулли, можно вывести формулу для нахождения наивероятнейшего числа появлений события:

(2)

Замечание. Длина промежутка, определяемого этими нера- венствами равна единице: , поэтому, если границы промежутка дробные, то определяется однозначно, если же целые - получаем два значения для .

Пример 4. Вероятность попадания в мишень при каждом выстреле равна 0,7. Найти наивероятнейшее число попаданий в мишень при 8 – ми выстрелах и определить вероятность такого числа попаданий.

В этом примере Тогда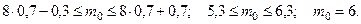

Теперь найдём вероятность:

§ 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ В СХЕМЕ БЕРНУЛЛИ.

Если число испытаний достаточно велико, то пользоваться формулой Бернулли не очень удобно. Представьте себе, что требуется вычислить такую вероятность:

Возникает вопрос, можно ли вычислить такую вероятность, не прибегая к формуле Бернулли. Оказывается можно. Для частного случая формула для приближённого вы -числения определённого числа появлений события 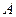для слу- чая большого числа независимых испытаний была найдена ещё в 1730 году Муавром, а в 1783 году эту формулу обоб -щил Лаплас для произвольного случая 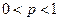. Поэтому ни- жеследующую теорему иногда называют теоремой Муавра – Лапласа. Доказательство её довольно громоздко, поэтому при- ведём только её формулировку и примеры.

Локальная теорема Лапласа. Если вероятность появления события 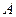в серии из 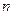независимых испытаний постоянна и удовлетворяет неравенству 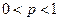, то вероятность того, что в этой серии испытаний событие появится ровно 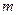раз приближённо вычисляется по формуле:

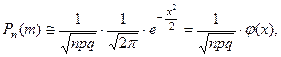(1)

где .

Во всех справочниках приведены таблицы для вычисления функции для положительных значений 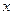, так как . Но, в принципе, значения этой функ- ции можно вычислить и непосредственно. Точность приближе- ния тем больше, чем больше .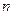

Пример 1. В среднем 95% часов, поступающих в продажу, не требуют дополнительной регулировки. Найти вероятность того, что из 300 часов, поступивших в продажу, не будет требовать дополнительной регулировки ровно 280.

Тогда , и получаем

Пример 2. Фирма по установке пластиковых окон расклады- вает рекламные листы по почтовым ящикам. В результате это- го примерно в одном случае из 1000 поступает заказ на изго-товление окна. Найти вероятность того, что при распростране- нии 100000 рекламных листов поступит 90 заказов.

Тогда и получаем

По мере увеличения числа испытаний вероятность того, что некоторое интересуемое нас событие произойдёт определён -ное точное количество раз становится очень близка к нулю, так как число возможных вариантов слишком велико. Поэтому чаще ставится задача определить вероятность того, что число появлений этого события заключено в некотором промежутке. В этом случае работает

Интегральная теорема Лапласа. Если вероятность появле- ния события 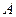(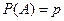) в серии из 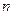независимых ис –пытаний постоянна, причём 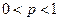, то вероятность того, что событие появится больше 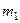, но меньше 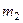раз приближён- но вычисляется по формуле:

(2)

где

Теорему доказывать не будем, но применяя эту теорему, также можем пользоваться специальной таблицей, тем более, что интеграл не вычисляется через элементарные функции. В таблицах приведены значения для функции , которую называют функцией Лапласа.

В таблицах приведены значения этой функ- ции для . При

Чтобы можно было пользоваться таблицей, преобразуем формулу (2)

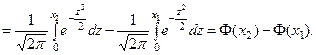
Таким образом, 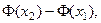где

Пример 3. В условиях примера 1, определить вероятность того, что не менее 280 часов не потребуют дополнительной регулировки, т.е. найти вероятность

По условию,

Тогда

Пример 4. В условиях примера 2, определить вероятность того, что поступит от 80 до 120 заказов на окна.

По условию,

Тогда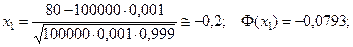

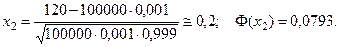
Следовательно,

Прямым следствием интегральной теоремы Лапласа являет- ся формула для вычисления вероятности отклонения отно -сительной частоты от постоянной вероятности в незави -симых испытаниях. Пусть произведено 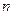независимых испы -

таний, в каждом из которых вероятность события 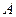постоян- на и 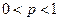. Тогда вероятность того, что относительная час- тота появления события отклонится от вероятности это- го событие по абсолютой величине не больше, чем на 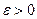вычисляется по формуле:

(3)

Пример 5. Вероятность того, что изготовленная деталь стан- дартна, равна 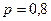. Найти вероятность того, что среди отобранных 900 деталей относительная частота стандартных деталей, по абсолютной величине, отклонится от вероятности не больше, чем на 0,04.

Тогда

Пример 6. Вероятность появления события в каждом из не -зависимых испытаний равна 0,2. Найти наименьшее число ис- пытаний 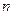, при которых с вероятностью 0,99 можно ожидать, что относительная частота появлений события отклонится от его вероятности по абсолютной величине не больше чем на 0,03.

По условию,

Тогда

По таблице значений функции Лапласа, видим, что Тогда

Пример 7. Отдел технического контроля проверяет 500 из- делий на брак. Вероятность бракованного изделия в проверяя- емой партии равна 0,02. С вероятностью 0,96 определить гра- ницы, в которых будет заключено число 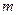бракованных изде- лий в данной партии.

Тогда

По таблице получаем и Таким образом, отклонение относительной часто –ты бракованных изделий от постоянной вероятности с вероят -ностью 0,96 удовлетворяет нераверству ,

или Так как 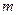- целое число, то получаем:

Сдедует заметить, что формулы Лапласа плохо работают, в таких случаях, когда вероятность события мала ), а число испытаний в опыте велико. В таких случаях удобно применять асимптотическую формулу Пуассона. Предположим, что в разных сериях испытаний произведение сохра- няет постоянное значение (т.е. среднее число появлений события в различных сериях испытаний при различных значениях 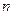остаётся неизменным). Тогда вероятность того, что при 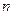испытаниях событие произойдёт раз вычисляя- ется по формуле Пуассона:

(3)

Рассмотрим несколько примеров:

Пример 8. Автоматическая телефонная станция в среднем за час получает 300 вызовов. Найти следующие вероятности: а) в данную минуту она получит ровно 3 вызова; б) в данную минуту она получит не менее 3 – х вызовов.

Определим среднее число вызовов в минуту .

Тогда, в случае а)

В случае б)

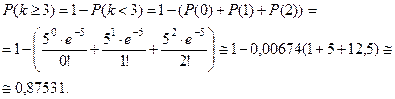
Пример 9. В банк прибыло 2000 пакетов денежных знаков. Вероятность того, что в определённом пакете содержится фальшивый денежный знак, равна 0,0002. Найти вероятность того, что при проверке будет обнаружено: а) ровно 4 фальшивых денежных знака; б) хотя бы один.

По условию,

Тогда, в случае а),

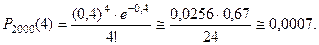
В случае б),

Пример 10. Среди семян пшеницы в среднем имеется 0,2% семян сорняков. Найти вероятность того, что при случайном отборе 3000 семян обнаружится 5 семян сорняков.

По условию, Тогда