Линейные дифференциальные уравнения. Метод вариации произвольной постоянной

Уравнение вида

где неизвестная функция, известные функции[2], называется линейным дифференциальным уравнением. Если то уравнение (1) называется однородным. Если то (1) называют неоднородным уравнением. Часто называют свободным членом уравнения (1) или неоднородностью.

Теорема 1. Пусть в уравнении (1) функции непрерывны на отрезке Тогда уравнение (1) с начальным условием имеет на отрезке

единственное решение и это решение может быть записано в виде

Доказательство. Найдем решение уравнения (1). Применим для этого так называемый метод вариации произвольной постоянной Лагранжа, который состоит в следующем.

Решим сначала однородное уравнение, соответствующее уравнению (1):

Затем вычислим решение уравнения (1), варьируя постоянную в решении однородного уравнения, т.е. будем определять решение уравнения (1) в виде где неизвестная функция. Подставляя предполагаемое решение в уравнение (1), будем иметь

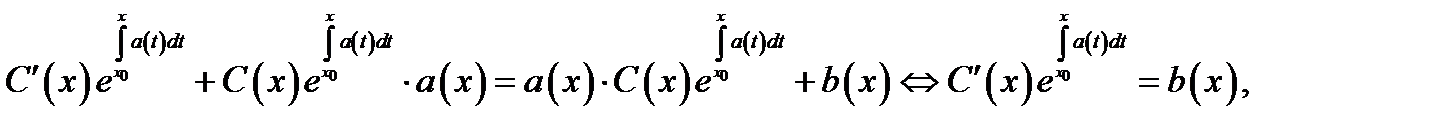
откуда находим Значит, общее решение уравнения (1) можно записать в виде

Подчиняя его начальному условию найдём, что Следовательно, решение уравнения (1) с начальным условием имеет вид (2). Теорема доказана.

Замечание 1. Так как второе слагаемое в есть частное решение (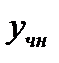) неоднород-

ного уравнения (1) (проверьте это!), а первое слагаемое суть общее решение соответствующего однородного уравнения, то для линейных дифференциальных уравнений имеет место утверждение: общее решение неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения, т.е.

Замечание 2. В отличие от нелинейных уравнений, имеющих, как правило, локальные решения, линейные дифференциальные уравнения имеют “глобальные решения,” т.е. они существуют на отрезке на котором непрерывны коэффициенты уравнения (1).

И наконец, отметим, что так называемое уравнение Бернулли:

приводится к линейному уравнению делением обеих частей на и дальнейшей заменой переменной

Пример 1 (Кузнецов Л.А. Типовые расчеты). Решить задачу Коши

Решение. Можно было бы сразу воспользоваться формулой (6), но мы ещё раз продемонстрируем метод Лагранжа. Найдём сначала общее решение соответствующего однородного уравнения:

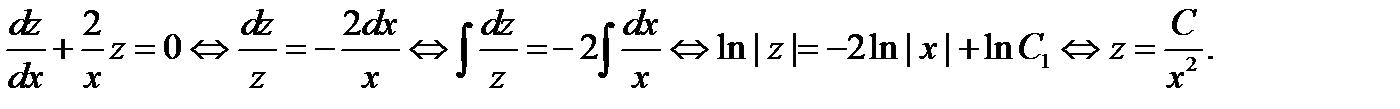
Вычисляя общее решение исходного уравнения в виде , будем иметь

Значит, общим решением данного неоднородного уравнения является функция

Подчиняя её начальному условию 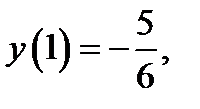будем иметь Следовательно, решением исходной задачи Коши будет функция

Если в уравнении порядок то это уравнение называют уравнением высшего порядка. Мы будем рассматривать уравнения высших порядков, разрешённые относительно старшей производной:

Областью определения уравнения (1) называется множество

{ имеет смысл }.