Дифференциальные уравнения с разделяющимися переменными. Однородные уравнения

Опишем теперь аналитические методы решения некоторых дифференциальных уравнений.

1. Уравнения с разделенными переменными: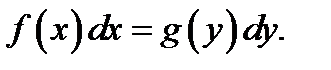

Ясно, что общий интеграл этого уравнения может быть получен интегрированием обеих частей (функции и 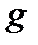непрерывны в своих областях определения):

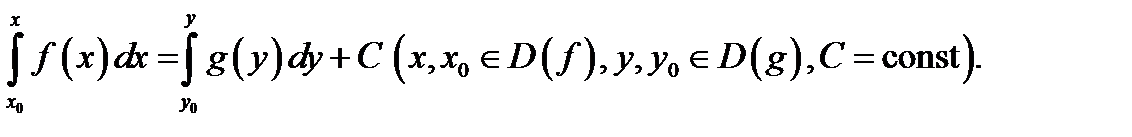
Отметим, что здесь часто вместо определенных интегралов пишут неопределенные.

2. Уравнения с разделяющимися переменными:

(здесь перед дифференциалами стоят произведения функций с разделёнными переменными).

Предполагая, что функции 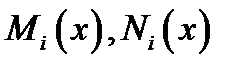непрерывны в своих областях определения, разделим обе части уравнения (4) на произведение 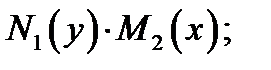будем иметь

Получено уравнение с разделёнными переменными. Интегрируя его, получим общий интеграл

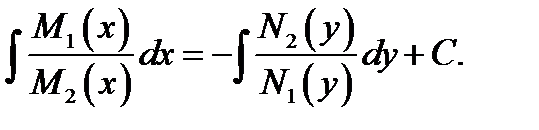
Однако это верно в случае, когда 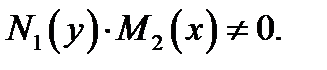Случа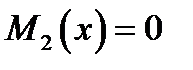и или 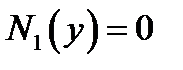надо рассматривать отдельно. Если при этом будут получены решения уравнения (4), то их надо присовокупить к уже полученным.

Пример 2. Решить уравнение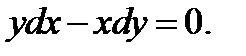

Решение. Разделяем переменные, поделив обе части уравнения на произведение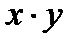

и интегрируем полученное уравнение:

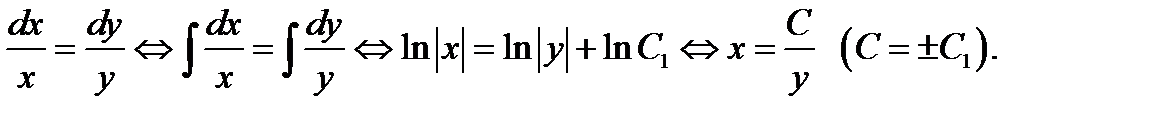
Рассматриваем отдельно случа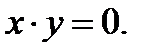й При 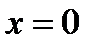исходное уравнение обращается в тождество, значит, 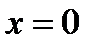– решение. Оно может быть получено из 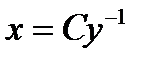при 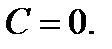Функция 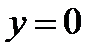также удовлетворяет данному уравнение. Однако она не может быть получена из 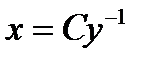. Следовательно, решениями исходного уравнения является совокупность функций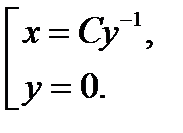

3. Однородные уравнения: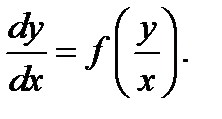

Такие уравнения приводятся к уравнению с разделяющимися переменной заменой 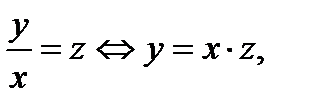где 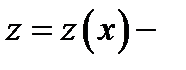новая неизвестная функция. Действительно, дифференцируя замену и подставляя её в исходное уравнение, будем иметь

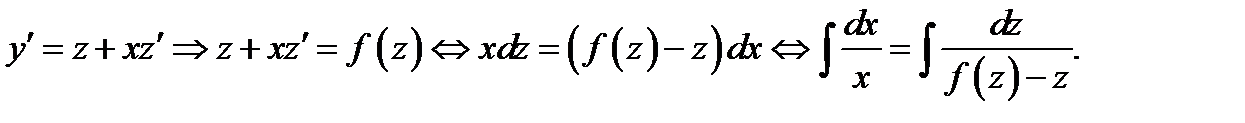
Заметим, что к однородным приводятся уравнения вида

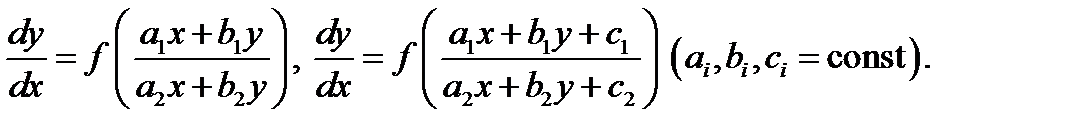
В первом случае надо разделить числитель и знаменатель входящей под знак функции дроби на 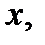во втором случае сделать замену переменных где решение системы уравнений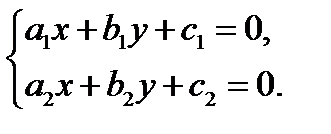

Пример 3. Решить уравнение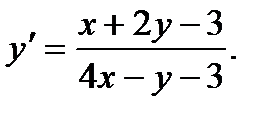

Решение. Найдем решение системы 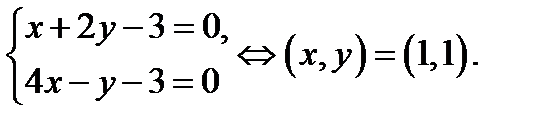Делаем замену переменных 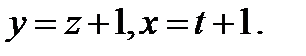Вместо исходного получим следующее уравнение:

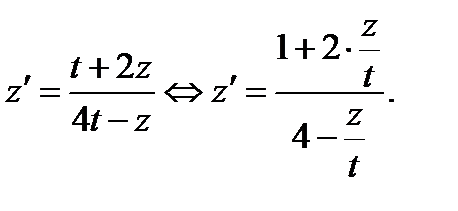jj

Это уравнение однородно, поэтому делаем замену 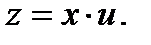В итоге получим уравнение 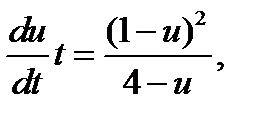решая которое методом разделения переменных, будем иметь

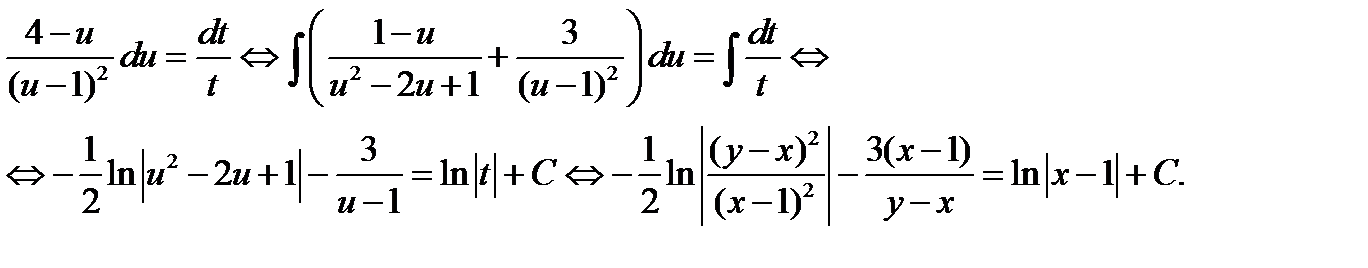
Получен общий интеграл данного уравнения.

Лекция 2. Линейные уравнения первого порядка. Дифференциальные уравнения высшего порядка. Задача Коши. Теорема существования и единственности решения задачи Коши. Общее решение и общий интеграл. Методы понижения порядка дифференциального уравнения

Наиболее часто встречаются линейные дифференциальные уравнения. Так называются уравнения, у которых правая часть линейна относительно неизвестной функции. Перейдём к их рассмотрению.