 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Работа против сил трения
|
|
Движущееся тело теряет энергию из-за наличия трения, которое действует на поверхности соприкосновения тел и и затрудняет их перемещение относительно друг друга.
 Сила трения направлена вдоль поверхности соприкосновения в сторону, противоположную движению Fтр = μFн, где μ – коэффициент трения, F н – нормальная сила, которая прижимает тело к опоре (не зависит от площади соприкосновения тел).
Сила трения направлена вдоль поверхности соприкосновения в сторону, противоположную движению Fтр = μFн, где μ – коэффициент трения, F н – нормальная сила, которая прижимает тело к опоре (не зависит от площади соприкосновения тел).
μ = tgα (при каком угле наклона тело начинает двигаться).
Сила трения равна скатывающей силе Fтр = Fс.
Виды трения: покоя (μ 0), скольжения (μ ск< μ 0), качения (μ к<< μ 0).
Если тело движется с постоянной скоростью равномерно против сил трения, то над ним совершается работа A тр = Fтр s = μFн s.
Работа против сил трения превращается в тепловую энергию.
Работа, затрачиваемая на упругую деформацию тела.
Согласно законам Ньютона все изменения состояния движения вызываются силами. Силы служат причиной либо ускорения тела (динамическое действие), либо изменения его формы (статическое действие).
Внешние силы изменяют форму тела – деформируют его вследствие относительного смещения элементов (молекул). Деформации, исчезающие с приращением действия силы – упругие деформации, тело возвращается к исходной форме. В пределах упругости вещества сила и деформация пропорциональны друг другу.
В этом случае справедлив закон Гука: действующей на тело (пружину) силе противодействует упругая сила F = - cx.
Коэффициент пропорциональности равен коэффициенту упругости (жесткость).
Упругость означает существование однозначной монотонно возрастающей функции, связывающей напряжение s = F/S (S - площадь поперечного сечения) и деформацию ε = x/l (x – относительное перемещение концов, l – длина образца): s = Е ε, Е – модуль упругости.
Пример изменения формы тела – изменение длины пружины. Изменение формы тела (деформация) вызывается относительным смещением элементов (молекул). Деформации, исчезающие с прекращением действия силы – упругие деформации. В пределах упругости вещества силы и деформации пропорциональны друг другу. В этом случае справедлив закон Гука.
Потенциальная энергия включает энергию положения и энергию упругой деформации.
Действующей на тело (пружину) силе противодействует упругая сила F = - с s, где с – жесткость пружины (с = F / s).
Если пружина растягивается на длину s, то действующая на пружину сила возрастет пропорционально s от 0 до Fмакс. Среднее значение силы равно 1/2 Fмакс.
Работа, затрачиваемая на деформацию пружины A = F/2 s, но F = -с s, тогда А = cs2/2, где с - жесткость тела или пружины. Эта работа запасается в виде потенциальной энергии упругой деформации (растянутой пружины): Wп = cs2/2.
Закон Гука является примером линейной зависимости перемещения от растягивающей силы F = - сx. Нелинейными упругими свойствами обладают, например, высокоэластичные резиновые шнуры – ели такой шнур растянуть в десять раз (ε = 0,9), а затем отпустить, он восстановит свою длину. Если длинные металлические проволоки подвергать малым деформациям (ε = 0,001), нелинейность не обнаруживается. При растяжении металлического стержня по мере возрастания растягивающего напряжения s деформация ε сначала растет по линейному закону. Это означает, что при таких ε первый член разложения функции s = f (ε) (полагая ее аналитической) в степенной ряд s = ε ∂f /∂ε + ½! ε2∂2f /∂ε2 +... значительно превосходит все остальные. Тогда s = Еε (Е – модуль упругости материала при его одноосном сжатии). Нелинейный закон – параболическая зависимость s = Аε - Вε2.
7.2 Уравнения движения
Одна из основных задач классической механики - задача прогнозирования движения различных тел и сред – решается на основе математической модели механического движения, которая представляет собой систему дифференциальных уравнений относительно координат и скоростей движущегося объекта. С помощью дифференциальных моделей решается большинство задач механики, гидродинамики, электродинамики и др.
Принцип независимости действия сил: если на материальную точку одновременно действует несколько сил, то каждая из них сообщает точке ускорение, определяемое 2-м законом Ньютона так, как если бы других сил не было, результирующее ускорение определяется действием результирующей силы.
Пример проекции сил.
Тело может находиться в равновесии, если сумма проекций приложенных к нему сил на любое направление равна нулю.
 F 1x = x1 – x2, F 2x = x2 – x3, F 3х = x3 – x1.
При равновесии сумма проекций сил равна нулю:
F 1x + F 2x + F 3х = 0.
F 1x = x1 – x2, F 2x = x2 – x3, F 3х = x3 – x1.
При равновесии сумма проекций сил равна нулю:
F 1x + F 2x + F 3х = 0.
| Действие трех сил на тело.
 Действующие силы: тяжести P = Mg, натяжения нити Т = mg, реакции (ограничивают движение тела) R. P 2 = Psinα = Mgsinα
Равновесие обеспечивается при Т = Р 2, R = Р 1.
Тогда условие равновесия:
Mgsinα = mg, Msinα = m.
Действующие силы: тяжести P = Mg, натяжения нити Т = mg, реакции (ограничивают движение тела) R. P 2 = Psinα = Mgsinα
Равновесие обеспечивается при Т = Р 2, R = Р 1.
Тогда условие равновесия:
Mgsinα = mg, Msinα = m.
|
 Вращение тела вокруг жесткой оси. Если сила F не проходит через ось вращения – на тело действует сила вращения. Сила F 1, которая проходит через ось вращения тела уравновешивается силой реакции R = F2. Вращение – только под действием силы F1, перпендикулярной линии, проходящей через точку А приложения силы и ось вращения О.
Вращение тела вокруг жесткой оси. Если сила F не проходит через ось вращения – на тело действует сила вращения. Сила F 1, которая проходит через ось вращения тела уравновешивается силой реакции R = F2. Вращение – только под действием силы F1, перпендикулярной линии, проходящей через точку А приложения силы и ось вращения О.
Для равновесия тела, закрепленного на оси, существенен не сам модуль силы, а произведение модуля на расстояние (плечо) – момент силы относительно оси: M = F 1 r. Если момент равен нулю – сила не вызывает вращения.
Согласно законам Ньютона все изменения состояния движения вызываются силами.
Уравнения движения определяют соотношения между скоростью, перемещением и временем.
Силу, как и любой вектор можно спроектировать на любую ось.
Уравнение движения материальной точки (системы точек) определяет связь ускорения wi и силы Fi, называется дифференциальным уравнением движения точки, и записывается в соответствии со вторым законом Ньютона:
m id2  / d t2 =
/ d t2 = 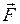 i (
i ( , d
, d  /d t, t), i = 1,..., N,
/d t, t), i = 1,..., N,
где m i - масса материальной точки, t > 0 – время,  - ее радиус-вектор,
- ее радиус-вектор, 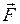 i - результирующая всех действующих на нее сил. Через
i - результирующая всех действующих на нее сил. Через  обозначено множество координат всех точек системы. Величины
обозначено множество координат всех точек системы. Величины 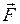 i считаются заданными и могут зависеть как от времени, так и от пространственных координат и скоростей всех рассматриваемых точек.
i считаются заданными и могут зависеть как от времени, так и от пространственных координат и скоростей всех рассматриваемых точек.
Величины 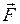 i считаются заданными и могут зависеть как от времени, так и от пространственных координат и скоростей всех рассматриваемых точек.
i считаются заданными и могут зависеть как от времени, так и от пространственных координат и скоростей всех рассматриваемых точек.
Силу, как и любой вектор, можно спроектировать на любую ось. Проекция вектора на ось равна разности координат начала и конца отрезка:
m 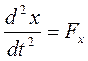 , m
, m  , m
, m 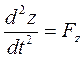 .
.
Различают два вида движения: поступательное и вращательное.
Дата публикования: 2014-11-04; Прочитано: 743 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
