Пример: хранение делящегося вещества

1. Формулировка содержательной модели.

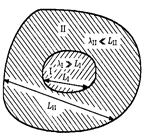
Объект моделирования: имеется некоторое количество радиоактивного вещества (область I), окруженного толстым слоем защитного материала (область II).

Формулировка цели исследований и задачи моделирования: разработать математическую модель, которая позволит определить закономерности изменения масс радиоактивного вещества и защиты.

Исходные данные: массы М _I(0), М _II(0) и размеры L _I(0), L _II(0) радиоактивного вещества и защитного материала, длина свободного пробега продуктов распада в радиоактивном материале λ_I и защите λ_II, μ_I - атомный вес радиоактивного вещества.

2. Формулировка концептуальной модели.

Формулировка закона, которому подчиняется явление: все, что вылетает из области радиоактивного вещества (области I) поглощается в области защиты (области II), и суммарная масса обоих веществ со временем не меняется – модель строится на основании закона сохранения материи.

Выделение существенных факторов и формулировка гипотез.

Все продукты распада, не испытывая столкновений с атомами вещества, покидают область I: длина свободного пробега продуктов распада λ_I значительно больше характерных размеров самого материала L_I, т.е. λ_I >> L_I, продукты деления полностью поглощаются в защите (области II). Это гарантируется при выполнении противоположного условия λ_II << L_II, где λ_II - длина пробега продуктов распада во втором веществе, L_II - его характерный размер.

3. Разработка математической модели.

В любой момент времени справедлив баланс

M_I (0) + M_II (0) = M_I (t) + M_II (t). (1)

Введение дополнительных гипотез.

Для определения текущих значений двух масс (замыкания математической формулировки задачи) необходимо привлечь дополнительное соображение о характере распада: число атомов радиоактивного вещества, распадающихся в единицу времени (скорость распада), пропорционально общему числу атомов вещества( чем больше самого вещества, тем больше продуктов распада).

Применим еще раз закон сохранения вещества к отрезку времени dt. За небольшое время dt между моментами t и t + dt всего распадется атомов

N_I (t + dt) – N_I (t) = - αN_I (t + ξdt), α>0, 0<ξ<1.

В этом уравнении, описывающем баланс атомов, в правой части стоит знак минус (вещество убывает), а величина N_I (t + ξdt) отвечает некоторому среднему значению числа атомов за рассматриваемое время, α – коэффициент пропорциональности.

Это же уравнение в дифференциальной форме:

dN_I (t) / dt = - αN_I (t).

Учитывая, что M_I (t) = μ_I N_I (t), где μ_I – атомный вес вещества I, получаем

dM_I (t)/ dt = - α M_I (t).(2)

Уравнения (1) и (2) вместе с условиями λ_I >> L_I и λ_II << L_II, а также величинами α, M_I (0), M_II (0) и составляют математическую модель рассматриваемого объекта.

Коэффициент пропорциональности (чем больше самого вещества, тем больше продуктов распада) определяется конкретным веществом.

4. Исследования модели и решение задачи.

Интегрируя (2) получаем, что масса делящегося вещества убывает по экспоненциальному закону

и при t → ∞ в области I вещество полностью исчезает.

Так как суммарная масса в соответствии с (1) остается постоянной, то в области II, количество вещества растет:

и при t → ∞ продукты распада полностью переходят из области I в область II.

Закон Архимеда – на погруженное в жидкость тело действует выталкивающая сила, равная весу жидкости, вытесненной телом:

F = gVρ ₀.

Сила приложена в центре тяжести объема погруженной части тела.