 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Рівняння площини, що проходить через три точки
|
|
Нехай в системі координат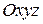 
задані три точки 
, 
, 
, що не лежать на одній прямій. Складемо рівняння лощини, що проходить через ці точки.
Для довільної точки 
, що належить цій площині, і тільки для точок цієї площини, вектори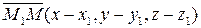 
, 
, 
компланарні, а отже їх мішаний добуток рівний нулю, тобто
або в координатній формі:
. (8.15)
Рівняння (8.15) називається рівнянням площини, що проходить через три точки.
Приклад 8.7. Скласти рівняння площини, що проходить через точки 
, 
, 
.
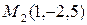Розв’язок. Підставимо координати точок 
, 
і 
в рівняння (8.15), отримаємо:
.
Так як
,
то рівняння площини приймає вигляд
або 
. t
Нехай площина відсікає на осях координат 
, 
, 
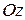відповідно відрізки 
, тобто проходить через три точки 
, 
, 
(рис.8.7). Підставивши координати цих точок в рівняння (8.15), отримаємо:
або
. (8.16)
Рівняння (8.16) називається рівнянням площини у відрізках, так як числа , вказують, які відрізки відсікає площина на осях координат.
Дата публикования: 2014-11-04; Прочитано: 3500 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
