 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Розв’язання типового варіанта. 1. Знайти область збіжності степеневого ряду
|
|
1. Знайти область збіжності степеневого ряду

► Даний степеневий ряд можна записати так:
 (11.20)
(11.20)
Застосуємо ознаку Даламбера:
 .
.
Як видно, ряд буде збігатись для тих значень х, для яких
 <1, або
<1, або  .
.
Дослідимо збіжність ряду на кінцях інтервалу.
При x =  , маємо числовий ряд:
, маємо числовий ряд:
 . (11.21)
. (11.21)
Ряд (11.21) є знакопереміжним. У силу ознаки Лейбніца даний ряд збігається, бо
1)  >
>  >
>  >
>  >… 2)
>… 2)  .
.
При x =  маємо числовий ряд
маємо числовий ряд
 .... (11.22)
.... (11.22)
Ряд (11.22) розбігається (для цього достатньо порівняти його з гармонічним рядом  .
.
Отже, значення x =  не належить області збіжності даного ряду.
не належить області збіжності даного ряду.
Таким чином,  - область збіжності досліджуваного ряду.
- область збіжності досліджуваного ряду.
2. Обчислити визначений інтеграл  з точністю до 0,001.
з точністю до 0,001.
► Обчислимо даний інтеграл наближено за допомогою рядів. Відомо, що
 .
.
Тоді
 ;
;
 .
.
Маємо


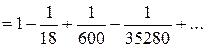 .
.
Отримано знакопереміжний числовий ряд, який задовольняє умовам теореми Лейбниця. Оскільки четвертий член цього ряду за абсолютним значенням менше ніж 0,001, достатньо обмежитись сумою перших трьох членів. Отже
 . ◄
. ◄
3. Обчислити наближено  з точністю до 0,0001.
з точністю до 0,0001.
► Скористаємось формулою
 ;
;
який є збіжним при  .
.
Запишемо заданий вираз у вигляді
 .
.
Для функції  маємо наступний розклад
маємо наступний розклад


Підставляючи замість х число  , отримає числовий ряд
, отримає числовий ряд

Маємо знакопереміжний числовий ряд. Щоб обчислити значення функції з точністю 0,0001, необхідно, щоб перший член, що відкидається, був менш, ніж 0,0001. Неважко обчислити, що
 .
.
Отже, 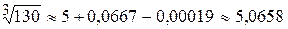 .
.
Дата публикования: 2014-11-04; Прочитано: 2958 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
