Элементы векторной алгебры

1. Вектором с началом в точке А и концом в точке В называется направленный отрезок.

2. Если и , то координаты вектора равны или .

3. Два вектора 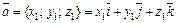и равны тогда и только тогда, когда

4. Сумма векторов 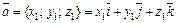и есть вектор .

5. Разность векторов 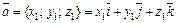и есть вектор .

6. Произведение вектора 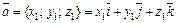на число есть вектор .

7. Длина вектора 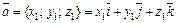есть число .

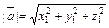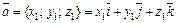8. Единичный вектор для вектора есть вектор .

9. Скалярное произведение векторов 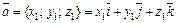и есть число , вычисляемое по формуле: .

10. Проекция вектора 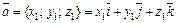на вектор есть число . Аналогично, .

11. Угол между векторам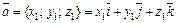и и вычисляется по формуле: .

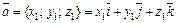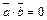12. Условие ортогональности двух векторов: векторы и ортогональны () тогда и только тогда, когда или .

13. Условие коллинеарности двух векторов: векторы 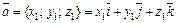и коллинеарные () тогда и только тогда, когда или .

14. Направляющие косинусы вектора 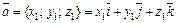соответственно равны , и , где a, b, g – углы между вектором и координатными осями Ox, Oy и Oz соответственно.

15. Векторное произведение векторов 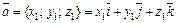и есть вектор .

16. Длина векторного произведения численно равна площади параллелограмма, построенного на векторах и как на сторонах (рис. 5), т. е. . Площадь треугольника, построенного на этих векторах, равна .

Рис. 5

17. Смешанное произведение векторов 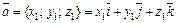, и есть число .

18. Условие компланарности трех векторов: векторы 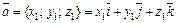, и компланарны тогда и только тогда, когда .

19. Смешанное произведение трех векторов , взятое по модулю, численно равно объему параллелепипеда, построенного на этих векторах как на ребрах (рис. 6), т. е. . Объем пирамиды, построенной на этих векторах, равен .

Рис. 6