 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Элементы линейной алгебры
|
|
Матрицы. Основные понятия и действия над ними
Матрицей называется упорядоченная таблица чисел (или массив чисел), содержащая m строк и n столбцов. Матрица записывается в виде

где индекс i обозначает номер строки, индекс j - номер столбца матрицы.
Числа, составляющие матрицу, называются ее элементами. Матрица, имеющая m строк и n столбцов, называется матрицей размера m ´ n.
Матрицы принято классифицировать по количеству их строк и столбцов.
Если число строк матрицы равно числу столбцов, m = n, то матрица называется квадратной порядка n.
Матрица размера m ´1 называется m -мерным (или m -компонентным) столбцом, матрица размера1´ n называется n -мерной (или n -компонентной) строкой (так называемые матрица-столбец и матрица-строка соответственно).
Среди квадратных матриц отметим диагональные матрицы, у которых все элементы с неравными индексами (i ¹ j) равны нулю
 .
.
Будем говорить, что элементы а 11, а 22, …, аnn расположены на главной диагонали.
Некоторые часто используемые матрицы с особыми значениями элементов, имеют специальные названия и обозначения.
Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается буквой Е
 .
.
Матрица, все элементы которой равны нулю, называется нулевой. Обозначается буквой О
 .
.
В матричном исчислении матрицы О и Е играют роль 0 и 1 в арифметике. Матрица размера 1´1, состоящая из одного числа, отождествляется с этим числом, т.е. (3)1´1 есть 3.
Квадратные матрицы, где все элементы расположены по одну сторону от главной диагонали, соответственно называются нижней и верхней треугольными матрицами.
Действия над матрицами
Две матрицы А и В одного и того же размера называются равными, если все их соответствующие элементы равны, т. е. aij = bij для всех i =  и j =
и j =  .
.
Суммой двух матриц Аm´n = (аij) и Вm´n = (bij) называется матрица Сm´n = (сij) такая, что сij = aij + bij, i =  , j =
, j =  . Операция вычисления матрицы С называется сложением матриц А и В.
. Операция вычисления матрицы С называется сложением матриц А и В.
Пример1. Найти сумму матриц А и В
 ,
,  .
.
Решение.
 .
.
Правило сложения двух матриц обобщается на случай любого конечного числа слагаемых матриц.
Произведением матрицы Аm´n = (аij) на число k называется матрица Вm´n = (bij) такая, что bij = kаij, i =  , j =
, j =  .
.
Пример2. Найти произведение матрицы А на число k
 , k = 5,
, k = 5,  .
.
Отметим, что умножать на число можно матрицу любого размера.
Замечание. В качестве всех или некоторых элементов матрицы возможно использование других математических объектов, для которых подходящим образом определены операции сравнения, сложения и умножения на число, например, векторы, функции или те же матрицы.
Определенные выше линейные операции обладают следующими свойствами:
1.  2.
2. 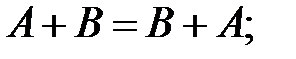 3.
3.  4.
4. 
| 5.  6.
6.  7.
7. 
|
где А, В и С - матрицы, a и b - числа.
Разность двух матриц А и В одинаковых размеров определяется равенством: А - В = А + (-1) В.
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной. Обозначается АТ.
Пример3. Транспонировать матрицы
 ,
, 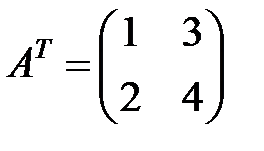 ;
;
 ,
, 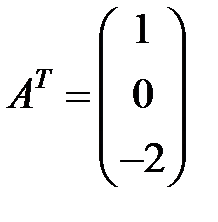 .
.
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
Умножить матрицу А = (аij) размера m ´ n на матрицу В = (bjk) размера n ´ q означает найти третью матрицу С = (сik) размера m ´ q, такую, что  , i = 1,2, …, m, k = 1,2, …, q.
, i = 1,2, …, m, k = 1,2, …, q.
Матрица С называется произведением матрицы А на матрицу В
С = АВ.
В общем случае, как следует из определения, элемент сik есть сумма произведений элементов i -ой строки на элементы k -го столбца.
Пример4. Перемножить матрицы
1) 

2)  .
.
Произведение двух матриц в общем случае зависит от порядка сомножителей, оно не коммутативно
 .
.
Пример5. Перемножить матрицы
 ;
;
 .
.
В частном случае равенство АВ = ВА возможно. Матрицы А и В, для которых выполняется равенство АВ = ВА, называются перестановочными или коммутативными.
Самым характерным примером может служить единичная матрица, которая является перестановочной с любой другой матрицей того же размера
А×Е = Е×А = А.
Перестановочными могут быть только квадратные матрицы одного и того же порядка. Очевидно, что для любых матриц выполняются следующее свойство
A×O = O×A = O,
где О – нулевая матрица.
Пример6. Матрицы
 ,
, 
перестановочные, так как легко проверить, что для них АВ = ВА.
Если матрицы А и В квадратные одного и того же порядка, то произведения АВ и ВА всегда существуют.
Произведение матриц обладает следующими свойствами:
1.  2.
2. 
| 3.  4.
4. 
|
Для операции транспонирования верны свойства:
1. 
2. 
Определение. Элементарными преобразованиями матриц назовем следующие преобразования:
1) умножение строки на число, отличное от нуля;
2) прибавление ко всем элементам одной строки соответствующих элементов другой строки, умноженных на одно и то же число;
3) перестановка строк;
4) вычеркивание (удаление) одной из одинаковых строк;
5) транспонирование;
Те же операции, применяемые для столбцов, также называются элементарными преобразованиями.
Две матрицы А и В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Записывается А ~ В.
Следует отметить, что равные и эквивалентные матрицы - понятия совершенно различные.
Дата публикования: 2014-11-04; Прочитано: 683 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
