Частотная характеристика границы раздела

Для достаточно больших углов падения светового пучка на плоскую границу раздела не удаётся получить связь между исходным распределением поля источника и его эквивалентным распределением источника в отсутствии границы раздела в явном виде для произвольной функции распределения комплексной амплитуды. В этом случае частотный спектр изображения получится в случае линейных систем в виде произведения спектра пространственных частот G(ω) функции распределения комплексной амплитуды поля объекта M(x) на частотную характеристику передающей системы. В общем случае следует учитывать ограниченность частотной характеристики свободного пространства, однако в пароксимальном рассмотрении это заведомо излишне, так как область рассматриваемых частот ω < k.

G^'(ω) = W(ω) G(ω), (3.1)

где G(ω), G'(ω) – спектры пространственных частот исходного и преобразованного поля соответственно. Следует отметить, что данное соотношение справедливо для линейных цепей, к которым нет основания причислять границу раздела (даже плоскую) в случае наклонного падения света. Действительно, связь между углом падения и преломления заведомо не линейна. Таким образом, если для нормального падения светового пучка частоты исходного и преобразованного полей совпадают, а преобразование спектра сводится к его линейной фильтрации, обусловленной существованием угловой зависимости пропускания границы раздела, то при наклонном падении светового пучка на границу раздела поворот плоскости локализации объекта, заданный в виде смещения в области пространственных частот на постоянную величину, не позволяет получить приближения удобные для анализа, а частоты исходного и преобразованного полей оказываются связанными не линейно. В связи со сказанным интерес представляет рассмотрение координатного преобразования осуществляемого границей раздела в спектральной области.

Пусть излучающий объект распложен в плоскости P(x₁) в среде с показателем U₁ (рисунок 11). Пусть также U₁(х₁) и U₂(х₂) – соответственно распределение комплексной амплитуды поля объекта и эквивалентного ему источника в отсутствии границы раздела, а

U₁(х₁) ↔ G₁(ω₁)

U₂(х₂) ↔ G₂(ω₂) (3.2)

- трансформанты Фурье,

где

Рисунок 11. Падение волны на плоскую границу раздела.

ω₁ = k₁ sin φ₁

ω₂ = k₂ sin φ₂ (3.3)

Тогда из закона Снеллиуса вытекает:

k₁sin(θ₁+φ₁) = k₂sin(θ₂+φ₂) (3.4)

или с учётом (3.3), после некоторых элементарных преобразований получим:

.(3.5)

Для больших углов падения и преломления в мало угловом приближении, то есть при

(3.6)

связь между частотами исходного и преобразованного полей представляется в виде:

,

откуда можно записать

(3.7)

При , дробь, в подкоренном выражении, удовлетворяет соотношению малости по сравнению с единицей и, разлагая корень в ряд по малости указанного выражения, для связи пространственных частот получим:

, (3.8)

, (3.9)

где .

Преобразование координат с точностью до квадратичных по отношению множителей оказывается взаимным. Таким образом, преобразование координат в спектре во втором приближении оказывается нелинейным и граница раздела не может быть рассмотрена в виде общего случая, в качестве элемента линейной цепи, а связь между спектрами исходного и преобразованного полей может быть представлена в виде:

. (3.10)

Таким образом, в частотной области спектр при преломлении из оптически более плотной в оптически менее плотную среду оказывается “растянут” и квадратично деформирован, что в действительности наблюдается на эксперименте, формально данное преобразование спектра может быть рассмотрено в виде интервала свёртки с δ-функцией Дирака:

. (3.11)

Где А(ω)- некоторая функция, определяющая изменение амплитуды поля вследствие неоднородного изменения масштаба в спектральной области. Вследствие закона сохранения можно записать для элементарного интервала пространственных частот ∆ω:

Ι(ω₁)∆ω₁=І(ω₂)∆ω₂

откуда

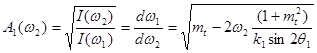. (3.12)

Если учесть пропускание границы раздела, как функцию угла падения, то из формулы Френеля следует, для волны, поляризованной перпендикулярно плоскости падения:

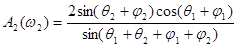. (3.13)

Из выражения следует, что производя учёт соотношений, можно получить зависимость пропускания границы раздела, как функцию частоты для малых φ₁ и φ₂:

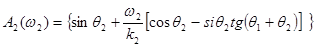. (3.14)

При построении плоского эквивалентного источника следует также учесть, что фазовый сдвиг обусловленный тем, что в лучевом приближении для преобразованного источника лучи не пересекаются в одной точке. Данное обстоятельство можно трактовать как сдвиг начала отсчёта в координатной плоскости эквивалентного источника для каждой гармоники на величину являющуюся функцией пространственной частоты. Приведение всех компонентов спектра пространственных частот к единой системе отсчёта можно осуществить путём введения фазового множителя:

. (3.15)

Из геометрических соображений (рис.) для величины сдвига можно получить выражение:

(3.16)

из выражения видно, что при использовании условия малости φ₁ и φ₂, а также использовании выражений (3.3) и (3.8) получаем:

, (3.17)

а положение эквивалентного источника определиться в виде:

. (3.18)

Таким образом, для связи спектров исходного и преобразованного полей можно записать, с учётом (3.10), (3.12), (3.13) и (3.17) с точностью до несущественного здесь частотного множителя

(3.19)

Данное выражение позволяет выделить следующие основные изменения в спектре при прохождении через границу раздела под углом, близким к углу полного внутреннего отражения наличие амплитудно-частотной характеристики, квадратичной по пространственной частоте, и, наконец, неоднородного преобразования координат в пространственно-частотной области.