Унитарные операторы

Линейный оператор 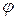унитарного пространства 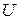называется унитарным, если он сохраняет скалярное произведение векторов, т. е.

.

Непосредственно из определения унитарного оператора следует:

,

т. е. тождественный оператор. Следовательно, унитарный оператор можно определить как оператор, для которого .

Так как , заключаем, что унитарный оператор является частным случаем нормального оператора.

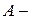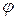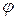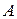Если матрица оператора в некотором ортонормированном базисе, то матрица будет сопряжено транспонированной. Условие унитарности оператора в матричной форме будет выглядеть следующим образом: или . Такая матрица тоже называется унитарной.

Если линейный оператор рассматривается в евклидовом пространстве и сохраняет скалярное произведение, то его матрица в некотором базисе будет такой, что , т. е. транспонированная матрица совпадает с обратной. Такой оператор называют ортогональным, а его матрицу 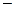ортогональной.

ТЕОРЕМА 1. Линейный оператор 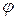унитарного пространства 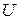является унитарным тогда и только тогда, когда он сохраняет длину вектора, т. е. .

ДОКАЗАТЕЛЬСТВО. Действительно,

.

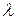В другую сторону, пусть . Тогда для любого справедливо: . Если 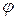сохраняет скалярное произведение, то . Раскрывая скобки и учитывая, что и , получим

(1)

При получаем

(2)

В случае евклидова пространства, т. к. , имеем .

Иначе, положим в (1) 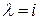, получим

.

Прибавим полученное равенство к (2), тогда . □

ТЕОРЕМА 2. Линейный оператор 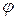унитарного пространства 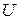является унитарным тогда и только тогда, когда 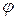переводит любой ортонормированный базис этого пространства снова в ортонормированный.

ДОКАЗАТЕЛЬСТВО. Пусть 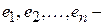ортонормированный базис пространства 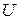. По определению унитарного пространства , значит, . А по предыдущей теореме .

Обратно, пусть

, , тогда . Так как по предположению 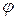переводит ортонормированный базис в ортонормированный, то

.

Следовательно, 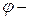унитарный оператор. □

ТЕОРЕМА 3. (основная об унитарных операторах). Матрица унитарного оператора 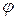в подходящем ортонормированном базисе является диагональной, с диагональными элементами, равными по модулю единице.

ДОКАЗАТЕЛЬСТВО. Так как 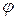является частным случаем нормального оператора, то по основной теореме о нормальных операторах, в некотором ортонормированном базисе он задаётся диагональной матрицей. Покажем, что собственные значения 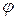по модулю равны 1.

Пусть 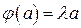. тогда

.

Но 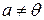, т. е. 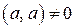. Значит, , т. е. . □