 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Уравнение Менделеева - Клапейрона
|
|
В состоянии термодинамического равновесия все параметры макроскопической системы остаются неизменными сколь угодно долго при неизменных внешних условиях. Эксперимент показывает, что для любых газов, находящихся при одинаковых внешних условиях в состоянии равновесия, независимо от сорта газов выполняется соотношение
 , (4.3. 1)
, (4.3. 1)
где  ,
,  ,
,  - давление, объем и число молекул первого и второго газа, соответственно. Полученное уравнение ( 4.3. 1 ) является справедливым, если давление газа не превышает нескольких атмосфер.
- давление, объем и число молекул первого и второго газа, соответственно. Полученное уравнение ( 4.3. 1 ) является справедливым, если давление газа не превышает нескольких атмосфер.
Параметр  , имеющий размерность энергии, растет с ростом температуры и является естественной мерой температуры. Однако исторически принято измерять температуру в градусах. В статистической физике и термодинамике используется абсолютная шкала температур, температура измеряется в кельвинах (К). Абсолютная температура
, имеющий размерность энергии, растет с ростом температуры и является естественной мерой температуры. Однако исторически принято измерять температуру в градусах. В статистической физике и термодинамике используется абсолютная шкала температур, температура измеряется в кельвинах (К). Абсолютная температура  связана с
связана с  соотношением
соотношением
 , (4.3. 2)
, (4.3. 2)
где  - постоянная Больцмана.
- постоянная Больцмана.
За абсолютный нуль температуры принимается температура, при которой объем газа приближается к нулю при постоянном давлении газа. Температура в кельвинах и температура в градусах Цельсия связаны следующим соотношением:
 . (4.3. 3)
. (4.3. 3)
Отсюда следует, что 
Число частиц газа  , с учетом этого соотношения и из определения параметра
, с учетом этого соотношения и из определения параметра  (4.3. 2), уравнение (4.2.1) принимает вид
(4.3. 2), уравнение (4.2.1) принимает вид
 , (4.3. 4)
, (4.3. 4)
где  - универсальная газовая постоянная. Уравнение (4.3.4) носит название уравнения состояния идеального газа или уравнения Менделеева-Клапейрона. Фактически оно было получено экспериментально для достаточно разреженных газов, т.е. для газов, в которых расстояния между молекулами значительно больше размеров молекул; на таких расстояниях молекулы газа практически не взаимодействуют, лишь при столкновениях молекул потенциальная энергия их взаимодействия становится сравнимой с кинетической энергией молекул, но столкновения происходят редко. Поэтому если в газе средняя потенциальная энергия взаимодействия молекул значительно меньше их средней кинетической энергии, то такой газ называется идеальным. С другой стороны, газ не может иметь слишком низкую плотность. Уравнение (4.3.4) справедливо, если выполняется следующее условие:
- универсальная газовая постоянная. Уравнение (4.3.4) носит название уравнения состояния идеального газа или уравнения Менделеева-Клапейрона. Фактически оно было получено экспериментально для достаточно разреженных газов, т.е. для газов, в которых расстояния между молекулами значительно больше размеров молекул; на таких расстояниях молекулы газа практически не взаимодействуют, лишь при столкновениях молекул потенциальная энергия их взаимодействия становится сравнимой с кинетической энергией молекул, но столкновения происходят редко. Поэтому если в газе средняя потенциальная энергия взаимодействия молекул значительно меньше их средней кинетической энергии, то такой газ называется идеальным. С другой стороны, газ не может иметь слишком низкую плотность. Уравнение (4.3.4) справедливо, если выполняется следующее условие:
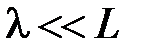 ,
,
где  характерный размер системы, например, размер сосуда, в котором заключен газ.
характерный размер системы, например, размер сосуда, в котором заключен газ.
Дата публикования: 2014-11-04; Прочитано: 613 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
