 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Движение заряженной частицы в однородном постоянном электрическом поле
|
|
В данном случае  и сила Лоренца имеет только электрическую составляющую
и сила Лоренца имеет только электрическую составляющую  . Уравнением движения частицы в этом случае является:
. Уравнением движения частицы в этом случае является:
 .
.
Рассмотрим две ситуации: а)  и б)
и б)  .
.
а)  (рис.13.1).
(рис.13.1).

Рис.13.1. Движение заряженной частицы в электрическом поле ( ).
).
Изменение кинетической энергии частицы на пути d происходит за счет работы силы  :
:
 , откуда
, откуда
где  - ускоряющее напряжение.
- ускоряющее напряжение.
В частности, если начальная скорость частицы  , то
, то
 .
.
Время пролета частицы в электрическом поле и пройденный путь находим из уравнений:

б)  (рис.13.2).
(рис.13.2).

Рис.13.2. Движение заряженной частицы в электрическом поле ( ).
).
В данном случае проекции уравнения движения частицы на координатные оси дают:
 .
.
Координаты частицы в момент времени t составляют:
 ;
;  .
.
Исключая из этих уравнений параметр t, находим уравнение траектории частицы:

Видим, что траекторией движения частицы является парабола.
Определим смещение следа частицы на экране, отстоящем от конденсатора на расстоянии b (рис.13.2):
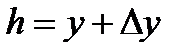 ,
,
где  - смещение частицы по вертикали, полученное ею в электрическом поле к моменту вылета из конденсатора
- смещение частицы по вертикали, полученное ею в электрическом поле к моменту вылета из конденсатора 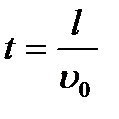 ;
;  - смещение частицы после вылета из конденсатора.
- смещение частицы после вылета из конденсатора.
Таким образом, имеем:
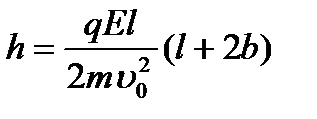 .
.
Дата публикования: 2014-11-04; Прочитано: 1052 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
