Граничные условия для магнитного поля

При переходе через границу раздела двух магнетиков с различными магнитными проницаемостями μ₁ и μ₂ силовые линии магнитного поля испытывают преломление (рис.11.2). Для того, чтобы выяснить, как происходит преломление линий поля необходимо установить для его нормальных и тангенциальных составляющих граничные условия. Вывод граничных условий для магнитного поля в точности аналогичен выводу граничных условий для электрического поля и основывается на применении основных теорем магнитостатики – теоремы Гаусса и теоремы о циркуляции магнитного поля.

h

h

Рис.11.2. К выводу граничных условий для магнитного поля.

Для нормальных составляющих индукции теорема Гаусса дает (см. рис.11.2):

,

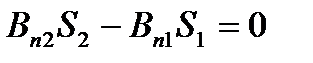где S₁ = S₂.

Поток индукции поля через боковую поверхность цилиндра при (переход к пограничному слою) становится исчезающе малым и им можно пренебречь. Следовательно, при переходе через границу раздела двух однородных магнетиков нормальные составляющие индукции магнитного поля непрерывны:

.

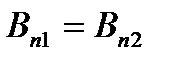Считая, что по границе раздела магнетиков не текут поверхностные токи (I = 0), будем иметь для тангенциальных составляющих напряженности магнитного поля, согласно теореме о циркуляции поля (рис.11.2):

,

где a₁ = а₂ = а.

Составляющие циркуляции поля по коротким сторонам контура обхода границы при (стягивание к границе) исчезают. Таким образом, приходим к выводу, что при переходе через границу раздела двух однородных магнетиков тангенциальные составляющие напряженности магнитного поля непрерывны:

.

Для построения картины преломления силовых линий поля на границе раздела двух магнетиков к полученным граничным условиям необходимо присоединить еще условия, вытекающие из материального уравнения, связывающего векторы и :

и .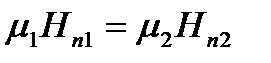

Тем самым, задача о преломлении линий поля полностью решается.