Законы сохранения и изменения импульса и момента импульса в механике

Система может состоять из одного тела.

Импульс материальной точки и системы материальных точек.

Как было сказано ранее, импульсом материальной точки называется произведение её массы на скорость: . Для системы из N материальных точек импульс системы равен сумме импульсов материальных точек, входящих в эту систему . Тело, которое нельзя считать материальной точкой, можно разделить на бесконечно малые объёмы и, перейдя от суммированию к интегрированию, получить: .

Поскольку радиус-вектор центра масс любого тела , то . Взяв производную по времени от обеих частей этого равенства, получаем . То есть, – импульс тела есть произведение массы тела на скорость движения центра масс. Таким образом, тело ведет себя как материальная точка, обладающая всей массой этого тела и находящаяся в центре масс.

Закон сохранения и изменения импульса материальной точки и системы материальных точек.

Рассмотрим замкнутую систему тел – материальных точек (рис. 1.5.1). Поскольку для каждой силы (i – номер тела, на которое действует сила, j – номер тела, со стороны которого действует сила) существует , то . Таким образом, сумма всех сил, действующих в замкнутой системе тел, равна нулю.

Рисунок 1.5.1. Силы, действующие в замкнутой системе тел.

По второму закону Ньютона . Отсюда и, следовательно, – суммарный импульс всех тел, входящих в замкнутую систему есть величина неизменная. Это выражает закон сохранения импульса. Этот закон действует только в инерциальных системах отсчёта.

Как было показано ранее, координаты центра инерции . Если считать массы тел неизменными, то можно взять производную . Из закона сохранения импульса получаем, что в инерциальной системе отсчёта скорость движения центра масс замкнутой системы тел неизменна вне зависимости от внутренних сил взаимодействия. А из этого следует, что система отсчёта, связанная с центром масс замкнутой системы тел является инерциальной.

Если система тел незамкнутая, то, кроме внутренних сил , действуют ещё и внешние силы 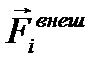со стороны тел, не входящих в систему (рис. 1.5.2). В этом случае полная сумма всех сил .

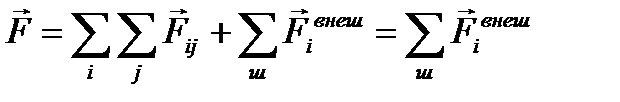Рисунок 1.5.2. Силы, действующие в незамкнутой системе тел.

Движение тел переменной массы

Представим себе ракету массой M, летящую равномерно и прямолинейно со скоростью до момента времени t (изображение (1) на рис. 1.5.1). В момент t включается двигатель и за время Δ t ракета приобретает дополнительную скорость (изображение (2) на рис. 1.5.3). Поскольку скорость ракеты изменяется, можно сказать, что на ракету действовала так называемая реактивная сила. Заметим, что за это время масса ракеты уменьшилась на Δ M за счет вылета горючих газов.

Рисунок 1.5.3. Реактивное движение

При этом на ракету могут действовать и иные силы (например, сила сопротивления атмосферы), которые на рис. 1.5.3 не показаны и равнодействующая которых равна . , а . Пусть из ракеты вылетают газы с постоянной скоростью u м/с относительно ракеты в количестве m кг/с. То есть .

Рассмотрим систему отсчёта, движущуюся со скоростью ракеты в данный момент времени. В этом случае p = 0.

Если промежуток времени устремить к нулю, то перейдём к дифференциалам. В проекции на ось x dp = -m × dt × u + md v, откуда ‑mu + m . Отсюда получаем – уравнение Мещерского. Величина – реактивная сила, действующая на тело переменной массы.

Если внешних сил нет, то ‑ u . При начальной скорости ракеты равной нулю . Отсюда .

начальная масса ракеты.

– формула Циолковского.

Таким образом, – максимальная скорость ракеты, где - масса топлива + масса окислителя.

1.5.5. Закон сохранения момента импульса.

Закон сохранения импульса: для замкнутой системы . Рассмотрим два взаимодействующих тела (рис. 1.5.4).

Введем характеристику – момент импульса тела относительно точки 0.

То есть - закон сохранения момента импульса

Если через точку 0 провести произвольную ось, то момент импульса тела (системы тел) относительно этой оси будет равен проекции момента импульса тела (системы тел) относительно точки 0 на эту ось.

Величина 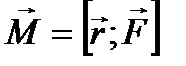- момент силы F относительно точки.

Момент силы относительно оси – аналогично моменту импульса.

Для всех внутренних сил

Т.о. получаем - основное уравнение динамики вращ. дв-я – аналог 2-го закона Ньютона.

Под действием за время dt гироскоп получает приращение момента импульса.

- то есть ось вращения гироскопа стала вращаться с угловой скоростью вокруг горизонтальной оси О – прецессия.

угловая скорость прецессии не зависит от угла между и