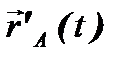Механика изучает механическое движение. Механическим движением называется изменение положения тел или частей тел относительно других тел или частей тел.
Уже из определения движения следует, что, во-первых, движение возможно только относительно чего-либо, во-вторых, для описания необходимо каким-то образом описывать положение, и, в-третьих, надо определить причины изменения положения. Описанием движения безотносительно к причинам занимается раздел физики, называемый кинематика, причинами же механического движения занимается динамика.
Кинематика
Расположение любого тела можно описывать по-разному. Современная (начиная с XVIII века) геометрия предлагает, а физика использует координатный способ. Координаты – это набор чисел, однозначно определяющий положение точки в пространстве. Минимально необходимое количество этих чисел называется размерностью пространства. В мире, где мы живём, размерность пространства равна трём: то есть если координат более трёх, то их можно придумать какие-то функции, сводящие их все к трём числам, и при этом положение точки будет описываться однозначно.
Система координат
Закон, по которому присваиваются координаты каждой точке пространства, носит название «системы координат». Существует бесконечное множество систем координат, но мы будем в основном использовать декартову прямоугольную систему.
Представим себе три взаимно перпендикулярные направленные прямые, пересекающиеся в одной точке (рис. 1.1.1), которым присвоены названия (1, 2, 3, или x, y, z, или как-нибудь ещё). Эти прямые называются осями координат, а точка O их пересечения – началом координат. Если с конца третьей прямой (то есть оттуда, куда смотрит стрелка) поворот от направления первой прямой к направлению второй виден как поворот против часовой стрелки, то такая система координат называется правой, а если по часовой стрелке – то левой. Как правило, пользуются правой системой координат.
Представим точку A в пространстве (рис. 1.1.2). Её положение можно описать через координаты радиус-вектора – вектора, который начинается в начале координат и заканчивается в точке A. Координатами будут служить длины отрезков r,, ry, rz отсекаемых на соответствующих осях перпендикулярами, опущенными из точки A. Можно также ввести понятие орта направления  – вектора, направленного вдоль данного направления, длина которого не имеет размерности и равна единице. В частности,
– вектора, направленного вдоль данного направления, длина которого не имеет размерности и равна единице. В частности,  ,
,  ,
,  – орты осей координат. Тогда координатами точки A будут служить коэффициенты r,, ry, rz в уравнении
– орты осей координат. Тогда координатами точки A будут служить коэффициенты r,, ry, rz в уравнении  . Оба определения дают одинаковый результат.
. Оба определения дают одинаковый результат.
| Рисунок 1.1.2. Координаты точки A в декартовой прямоугольной системе координат
|
В декартовой прямоугольной системе координат очень просто определяются модуль вектора (здесь и в дальнейшем модуль вектора будет обозначаться тем же символом, но без стрелки):
 ,
,
скалярное произведение векторов:
 ,
,
векторное произведение векторов:
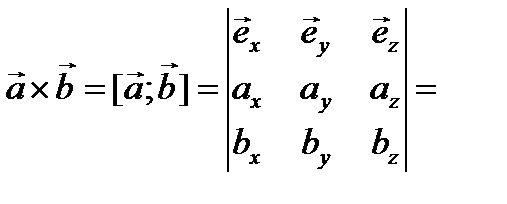
 .
.
Система отсчета
Все физические процессы – то есть, все виды движения – протекают во времени. Соединение системы координат и способа отсчета времени называется системой отсчета. Механическое движение материальной точки (или какой-либо точки тела) в таком случае задаётся зависимостью радиус-вектора (или координат) от времени t:
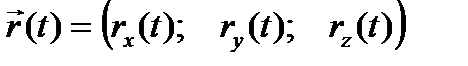
Переход из одной системы отсчета в другую в классической (нерелятивистской) механике
Пусть заданы две системы отсчета: xyz и x’y’z’ (рис. 1.1.3). В классической физике пространство считается однородным и изотропным и его свойства, равно как и течение времени, одинаковы во всех системах. Поэтому
t = t’ + const,
 .
.
| Рисунок 1.1.3. Переход из одной системы отсчёта в другую
|
Единицы измерения
Для того, чтобы иметь возможность сравнивать физические величины, необходимо иметь эталонные значения. Выбор эталона, вообще говоря, процесс произвольный. Однако, единожды выбрав, в дальнейшем следует использовать одну и ту же систему единиц – иначе будут большие сложности при расчетах. В 1981 году государственный стандарт ГОСТ 8.417-81 вводит как обязательную Международную систему единиц (обозначаемую SI или СИ). Основными единицами СИ являются: для времени – секунда (обозначения: российское – с, международное – s), равная сумме 9192631770 периодов излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133, или примерно 1/86400 средних суток; для расстояния – метр (обозначения: российское – м, международное – m), равный по длите бруску из платино-иридиевого сплава, хранящегося в Международном бюро мер и весов в г. Севр, Франция (вблизи Парижа). Один метр примерно равен 1/40000000 земного меридиана или, точнее, расстоянию, которое свет проходит в вакууме за 1/299792458 долю секунды. Определения других основных единиц СИ будут даны по мере их появления в данном курсе.
Система СИ позволяет использовать специальные приставки для обозначения кратных и дробных единиц (табл. 1.1.1)
Таблица 1.1.1
| Множитель
| Приставка
| Множитель
| Приставка
|
| Наименование
| Обозначение
| Наименование
| Обозначение
|
| российское
| международное
| российское
| международное
|
| 101
| дека
| да
| da
| 10‑1
| деци
| д
| d
|
| 102
| гекто
| г
| h
| 10‑2
| санти
| с
| c
|
| 103
| кило
| к
| k
| 10‑3
| милли
| м
| m
|
| 106
| мега
| М
| M
| 10‑6
| микро
| мк
| μ
|
| 109
| гига
| Г
| G
| 10‑9
| нано
| н
| n
|
| 1012
| тера
| Т
| T
| 10‑12
| пико
| п
| p
|
| 1015
| пета
| П
| P
| 10‑15
| фемто
| ф
| f
|
| 1018
| экса
| Э
| E
| 10‑18
| атто
| а
| a
|

 – вектора, направленного вдоль данного направления, длина которого не имеет размерности и равна единице. В частности,
– вектора, направленного вдоль данного направления, длина которого не имеет размерности и равна единице. В частности,  ,
,  ,
,  – орты осей координат. Тогда координатами точки A будут служить коэффициенты r,, ry, rz в уравнении
– орты осей координат. Тогда координатами точки A будут служить коэффициенты r,, ry, rz в уравнении  . Оба определения дают одинаковый результат.
. Оба определения дают одинаковый результат.



 ,
, ,
,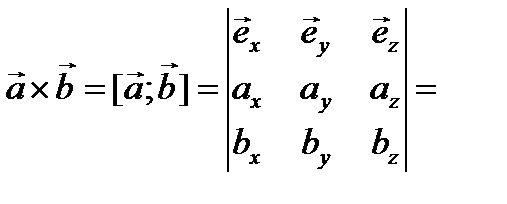
 .
.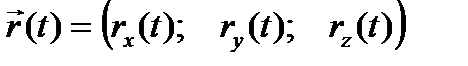
 .
.