Инертность тел. Масса. Импульс. Взаимодействие тел. Сила. Законы Ньютона. Виды сил в механике. Силы тяготения. Реакция опоры и вес. Сила упругости. Сила трения. Деформация упругих твердых тел. Основные виды деформации. Одноосное растяжение и сжатие. Деформация сдвига, кручения и изгиба. Упругие деформации. Законы Гука. Модуль Юнга и модуль сдвига. Пластическая деформация твердых тел. Предел прочности.
Инерциальные и неинерциальные системы отсчета. Принцип относительности Галилея. Преобразования Галилея. Силы инерции при поступательном и вращательном движении. Принцип эквивалентности сил инерции и силы тяжести (инертной и гравитационной масс).
Инертность.
Жизненный опыт свидетельствует, что одно и то же воздействие вызывает различное изменение в параметрах движения различных тел. Так, порыв ветра подхватывает и сильно ускоряет воздушный шарик, немного разгоняет футбольный мяч и практически не вызывает никаких видимых изменений в поведении камня – притом, что указанные три предмета имеют одинаковые размеры и форму. Экспериментально доказано, что отличительный признак, определяющий различие в изменении скорости – это масса: чем она больше, чем изменение скорости меньше при одном и том же внешнем воздействии. То есть величина  одинакова для всех тел, подвергшихся одинаковым по интенсивности и продолжительности воздействиям. Склонность тела сохранять параметры своего движения называется инертность. Таким образом, масса есть мера инертности тела.
одинакова для всех тел, подвергшихся одинаковым по интенсивности и продолжительности воздействиям. Склонность тела сохранять параметры своего движения называется инертность. Таким образом, масса есть мера инертности тела.
В системе СИ масса измеряется в килограммах (кг). Один килограмм – это масса эталона, хранящегося в Палате мер и весов в Севре (Франция), одна двенадцатая от суммарной массы 6,022·1026 атомов изотопа углерода‑12 или масса 1·10‑3 м3 воды при температуре +40C.
Произведение массы тела на его скорость именуется импульсом тела:  . В системе СИ импульс измеряется в кг·м/с.
. В системе СИ импульс измеряется в кг·м/с.
Следует отметить, что сказанное про массу и изменение скорости верно не во всех системах, а только в тех, где при отсутствии внешних воздействий скорость движения тел не меняется. Такие системы отсчета, в которых не меняются вектора скорости всех тел, которые не испытывают внешних воздействий (или внешние воздействия скомпенсированы) называются инерциальными. Понятие инерции введено Галилео Галилеем в 1632 году.
Законы Ньютона
Исаак Ньютон постулировал, что существуют инерциальные системы отсчёта. Это утверждение называют первым законом Ньютона. Этот закон не даёт указаний, сколько таких систем, как их искать, но заявляет сам факт их существования.
Внешнее воздействие на любое тело, о котором говорилось выше, следует как-то измерять. Величина, именуемая силой, вводится в качестве меры интенсивности воздействия. Второй закон Ньютона гласит, что величина силы, действующей на тело, равна быстроте изменения импульса этого тела:  . Если записать это выражение как
. Если записать это выражение как  и назвать величину
и назвать величину  импульсом силы, то формулировка второго закона Ньютона будет: импульс силы, действующей на тело, равен изменению импульса тела.
импульсом силы, то формулировка второго закона Ньютона будет: импульс силы, действующей на тело, равен изменению импульса тела.
На одно и то же тело может одновременно оказываться несколько воздействий. В этом случае принцип суперпозиции гласит, что силы складываются как вектора (рис. 1.3.1).
| Рисунок 1.3.1. Сложение сил.
|
Опыт показывает, что во всех случаях воздействие на какое-либо тело оказывает другое тело (или несколько тел), и это другое тело также подвергается воздействию со стороны первого тела. То есть любое воздействие является взаимодействием. Третий закон Ньютона гласит, что силы, с которыми воздействуют друг на друга взаимодействующие тела равны по величине и противоположны по направлению.
| Рисунок 1.3.2. Третий закон Ньютона.
|
Виды сил в механике
Сила тяготения
Закон всемирного тяготения гласит, что любые тела (материальные точки) притягиваются с силой, направленной вдоль линии, их соединяющей, пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними (рис. 1.3.3):
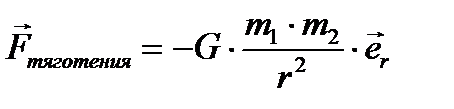
| Рисунок 1.3.3. К закону всемирного тяготения.
|
Можно доказать, что эта же формула верна не только для материальных точек, но и для любых сферически симметричных тел (сфер, шаров, сферических слоёв).
Как видно из формулы, тело с массой m 2 характеризуется только самой величиной массы, а всё остальное относится только к телу с массой m 1 и пространственному расположению тел. Можно считать, что это всё остальное характеризует поле, предающее воздействие от тела с массой m 1 на тело с массой m 2. Эта характеристика поля называется напряженностью  :
:
 ;
; 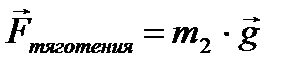
По второму закону Ньютона любая сила, действующая на тело массой m 2:  , следовательно
, следовательно  – напряженность гравитационного поля равна ускорению, с которым будет двигаться тело массой m 2 по направлению к телу массой m 1, при условии, что других сил нет. Это ускорение называется ускорением свободного падения.
– напряженность гравитационного поля равна ускорению, с которым будет двигаться тело массой m 2 по направлению к телу массой m 1, при условии, что других сил нет. Это ускорение называется ускорением свободного падения.
Заметим, что масса как мера инерции, входящая в уравнение для второго закона Ньютона, в точности равна массе как мере гравитации, входящей в закон всемирного тяготения. Это утверждение носит название принципа эквивалентности инертной и гравитационной масс и подтверждено с высокой точностью многочисленными экспериментами.
Сила тяжести
В тех задачах, где изменение расстояния между центрами гравитационно взаимодействующих тел намного меньше самого расстояния, величину изменения  обычно можно считать несущественной и принимать
обычно можно считать несущественной и принимать  для всех точек пространства, описываемых в задаче. Поэтому просто записывают, что сила тяжести
для всех точек пространства, описываемых в задаче. Поэтому просто записывают, что сила тяжести 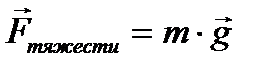
Реакция опоры и вес
Если тело находится под действием силы тяжести (силы тяготения), но не падает с ускорением  , следовательно, на него действуют и иные силы. Как правило, это сила нормальной реакции опоры
, следовательно, на него действуют и иные силы. Как правило, это сила нормальной реакции опоры  , которая всегда перпендикулярна поверхности взаимодействия тел, или сила натяжения подвеса
, которая всегда перпендикулярна поверхности взаимодействия тел, или сила натяжения подвеса 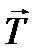 (рис. 1.3.4). Видно, что
(рис. 1.3.4). Видно, что  (рис. 1.3.4 б) и
(рис. 1.3.4 б) и  (рис. 1.3.4 г) не всегда направлены вдоль одной прямой с
(рис. 1.3.4 г) не всегда направлены вдоль одной прямой с  и не всегда равны ей по модулю.
и не всегда равны ей по модулю.
Вес тела  – это сила, с которой тело давит на опору или натягивает подвес. Следовательно, вес приложен к опоре или подвесу, равен по модулю и противоположен по направлению силе нормальной реакции опоры (
– это сила, с которой тело давит на опору или натягивает подвес. Следовательно, вес приложен к опоре или подвесу, равен по модулю и противоположен по направлению силе нормальной реакции опоры ( ).
).
Рисунок 1.3.5. Направления сил тяжести  , веса тела , веса тела  , нормальной реакции опоры , нормальной реакции опоры  (а, б) и натяжения подвеса (а, б) и натяжения подвеса  (в, г). (в, г).
|
Сила трения
Под названием сила трения понимают несколько различных по природе и по способу расчёта сил. Выделяют два типа сил трения: сухого и вязкого. Сил сухого трения – три вида.
Во-первых, это сила трения покоя, которая возникает, когда вдоль границы раздела двух тел, неподвижных друг относительно друга (рис. 1.3.6). При этом и скорость, и ускорение равны нулю, поэтому  , где
, где  – все прочие силы. Когда сила сухого трения скольжения достигает максимально возможной (предельной) величины, то тела начинают двигаться друг относительно друга. Эта предельная величина рассчитывается по формуле
– все прочие силы. Когда сила сухого трения скольжения достигает максимально возможной (предельной) величины, то тела начинают двигаться друг относительно друга. Эта предельная величина рассчитывается по формуле
 ,
,
где  – коэффициент трения покоя, зависящий только от природы контактирующих веществ, качества поверхностей и от температуры.
– коэффициент трения покоя, зависящий только от природы контактирующих веществ, качества поверхностей и от температуры.
| Рисунок 1.3.6. Сила сухого трения.
|
Во-вторых, это сила сухого трения скольжения. Схема, поясняющая её направление, совпадает со схемой на рис.1.3.6. Величина этой силы рассчитывается по формуле:  , где коэффициент трения
, где коэффициент трения  зависит только от природы контактирующих веществ, качества поверхностей и от температуры. Вообще говоря, обычно
зависит только от природы контактирующих веществ, качества поверхностей и от температуры. Вообще говоря, обычно 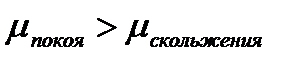 , однако в большинстве задач эти коэффициенты считаются равными.
, однако в большинстве задач эти коэффициенты считаются равными.
В-третьих, это сила трения качения (рис. 1.3.7). Видно, что перемещению катящегося тела мешает образование углубления под ним и «горки» перед ним. Величина силы трения качения рассчитывается по формуле:  , где коэффициент трения
, где коэффициент трения  зависит только от природы контактирующих веществ, качества поверхностей и от температуры. Обычно
зависит только от природы контактирующих веществ, качества поверхностей и от температуры. Обычно  .
.
| Рисунок 1.3.7. Причина появления силы трения качения
|
Природа всех видов сил сухого трения сходная: во-первых, прижатые (например, под действием силы тяжести) тела деформируют свои поверхности и меньшее тело оказывается в некотором углублении (рис. 1.3.8а), во вторых, контактирующие поверхности имеют шероховатости, мешающие взаимному перемещению (рис. 1.3.8б), в третьих, в зонах контакта могут возникать межатомные связи, которые должны рваться при перемещении:
| Рисунок 1.3.8. Причины появления сил трения на контактирующих поверхностях: деформация тел (а), шероховатость поверхностей (б).
|
Сила упругости и деформация твердых тел
Когда на любое реальное тело оказывается внешнее воздействие, изменяется внутреннее строение этого тела. Для твердого тела характерна некоторая (большая или меньшая в зависимости от условий) направленность связей между соседними атомами. Поэтому, когда небольшие внешние воздействия несильно изменяют направление этих межатомных связей, в теле возникает сила, старающаяся сохранить “status quo” в направлениях связей – сила упругости. Величина этой силы (рис. 1.3.9) подчиняется закону Гука:
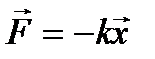 ,
,
где  – перемещение конца стержня, то есть удлинение стержня, k – жёсткость стержня.
– перемещение конца стержня, то есть удлинение стержня, k – жёсткость стержня.
| Рисунок 1.3.8. Возникновение силы упругости: тёмным цветом обозначено исходное, светлым – растянутое состояние стержня
|
Опыты показали, что для стержня жесткость k зависит как от геометрических размеров: начальной длины l 0 и начальной площади поперечного сечения S 0, так и от модуля упругости материала E (он же модуль Гука, он же модуль эластичности).
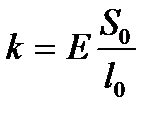
Этот модуль не зависит от геометрических размеров и формы объекта и определяется составом и строением материала. С ростом температуры модуль упругости E уменьшается, причём практически для всех материалов от 0 К до температуры плавления он уменьшается примерно в 2 раза.
Сила упругости: 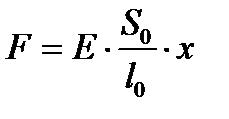 .
.
Величина  называется механическим растягивающим напряжением, измеряется в Паскалях (Па),
называется механическим растягивающим напряжением, измеряется в Паскалях (Па),  . Величина
. Величина 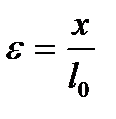 называется относительной деформацией, измеряется в долях или процентах.
называется относительной деформацией, измеряется в долях или процентах.
Упругая деформация после снятия внешней нагрузки полностью снимается. Однако, если внешняя нагрузка достаточно велика, то, во-первых, перестаёт выполняться закон Гука – связь между механическим напряжением и относительной деформацией перестаёт быть линейной, а во-вторых, после снятия внешней нагрузки не вся деформация снимается – часть деформации остаётся. Эта остаточная деформация называется пластической (рис.1.3.9). Когда же прикладываемое напряжение становится равным временному сопротивлению разрыву, происходит так называемое нарушение однородности деформации – в каком-то месте образца образуется сужение (шейка) и при дальнейшем увеличении деформации образец разрушается.
| Рисунок 1.3.9. Диаграмма растяжения (схема): σупр – предел упругости, σв – предел прочности (временное сопротивление разрыву), εост – остаточная пластическая деформация.
|

Инерциальные и неинерциальные системы отсчета
Первый закон Ньютона утверждает, что существуют инерциальные системы отсчёта. Предположим, что нам известна одна инерциальная система отсчёта (нештрихованная – рис. 1.3.10).
| Рисунок 1.3.10. Переход из инерциальной системы отсчёта в другую
|
Как видно из рисунка 1.2.10:  . Поскольку это равенство выполняется всегда, то и производные по времени от обеих частей тоже равны:
. Поскольку это равенство выполняется всегда, то и производные по времени от обеих частей тоже равны:  , – или, что то же самое:
, – или, что то же самое:  .Аналогично, взяв производную от скорости по времени, получаем:
.Аналогично, взяв производную от скорости по времени, получаем:  .
.
Предположим, что в инерциальной системе отсчёта на тело A не действуют другие тела. Тогда это тело движется в нештрихованной системе отсчёта равномерно и прямолинейно и  . Если штрихованная система отсчёта также является инерциальной, то и
. Если штрихованная система отсчёта также является инерциальной, то и  , а следовательно и
, а следовательно и  . То есть, система отсчёта, движущаяся относительно инерциальной поступательно без ускорения (иными словами, равномерно и прямолинейно) сама является инерциальной.
. То есть, система отсчёта, движущаяся относительно инерциальной поступательно без ускорения (иными словами, равномерно и прямолинейно) сама является инерциальной.
Принцип относительности Галилея и преобразования Галилея
Если у нас обе системы инерциальные (то есть  ) и тело A движется с ускорением
) и тело A движется с ускорением  , то
, то  – ускорение инвариантно по отношению к переходу из одной инерциальной системы отсчёта в другую. Ускорения появляются при наличии силы, действующей на тело A:
– ускорение инвариантно по отношению к переходу из одной инерциальной системы отсчёта в другую. Ускорения появляются при наличии силы, действующей на тело A:  . То есть, при переходе из одной инерциальной системы отсчёта в другую силы, действующие на тела, не меняются. А следовательно, выполняется принцип относительности Галилея: все механические явления в различных инерциальных системах отсчёта протекают одинаковым образом, вследствие чего никакими механическими опытами невозможно установить, покоится ли данная система отсчёта или движется равномерно и прямолинейно. Поскольку
. То есть, при переходе из одной инерциальной системы отсчёта в другую силы, действующие на тела, не меняются. А следовательно, выполняется принцип относительности Галилея: все механические явления в различных инерциальных системах отсчёта протекают одинаковым образом, вследствие чего никакими механическими опытами невозможно установить, покоится ли данная система отсчёта или движется равномерно и прямолинейно. Поскольку  , то
, то  – преобразование Галилея.
– преобразование Галилея.
Силы инерции при поступательном и вращательном движении
Если нештрихованная система инерциальная, а штрихованная - енинерциальная (то есть  ) и тело A в инерциальной системе движется с ускорением
) и тело A в инерциальной системе движется с ускорением  , то
, то  . Умножим все части уравнения на массу тела A:
. Умножим все части уравнения на массу тела A:  . Поскольку
. Поскольку  , то
, то  . Д’Аламбер предложил ввести понятие фиктивной силы инерции
. Д’Аламбер предложил ввести понятие фиктивной силы инерции  . Отличие силы инерции от реальных сил в том, что нет никакого тела, которое действует на изучаемое тело и, следовательно, в отношении силы инерции нельзя говорить о выполнимости третьего закона Ньютона. Однако понятие силы инерции очень удобно, поскольку для расчёта ускорения в неинерциальной системе отсчёта можно пользоваться формулой
. Отличие силы инерции от реальных сил в том, что нет никакого тела, которое действует на изучаемое тело и, следовательно, в отношении силы инерции нельзя говорить о выполнимости третьего закона Ньютона. Однако понятие силы инерции очень удобно, поскольку для расчёта ускорения в неинерциальной системе отсчёта можно пользоваться формулой  , понимая под
, понимая под  сумму реальных сил и силы инерции.
сумму реальных сил и силы инерции.
При поступательном движении неинерциальной системы отсчёта относительно инерциальной системы ускорение  одинаково для всех точек пространства. Если же неинерциальная система вращается, то это не так. Рассмотрим случай, когда оси z и z’ совпадают и штрихованная система вращается относительно инерциальной нештрихованной с постоянной угловой скоростью
одинаково для всех точек пространства. Если же неинерциальная система вращается, то это не так. Рассмотрим случай, когда оси z и z’ совпадают и штрихованная система вращается относительно инерциальной нештрихованной с постоянной угловой скоростью  (рис. 1.3.11). Пусть тело массой m находится в точке A, неподвижной во вращающейся (штрихованной) системе отсчёта. В этом случае радиус-вектор точки A
(рис. 1.3.11). Пусть тело массой m находится в точке A, неподвижной во вращающейся (штрихованной) системе отсчёта. В этом случае радиус-вектор точки A  , где R – расстояние от начала координат до точки А. При этом орт координаты x’
, где R – расстояние от начала координат до точки А. При этом орт координаты x’  , а орт координаты y’
, а орт координаты y’  .
.
| Рисунок 1.3.11. Инерциальная и неинерциальная вращающаяся системы отсчёта.
|
Заметим, что  , а
, а  Скорость точки А:
Скорость точки А:  , а ускорение
, а ускорение
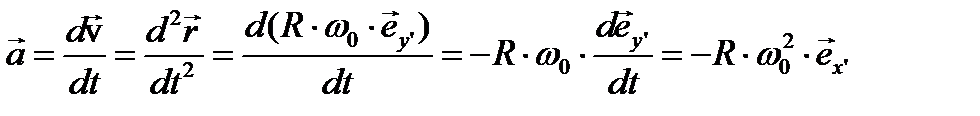 . Следовательно, в инерциальной системе на это тело действует сила
. Следовательно, в инерциальной системе на это тело действует сила  , направленная к центру вращения. Поскольку тело A в неинерциальной системе отсчёта неподвижно, то
, направленная к центру вращения. Поскольку тело A в неинерциальной системе отсчёта неподвижно, то  и
и  . Отсюда
. Отсюда  и направлена от центра вращения. Такая сила инерции называется центробежной
и направлена от центра вращения. Такая сила инерции называется центробежной 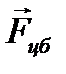 .
.
Рассмотрим случай, когда тело A движется от центра вращения вдоль оси x’ с постоянной скоростью v’. Тогда  ,
,  , а
, а  . Следовательно, в инерциальной системе на это тело действует сила
. Следовательно, в инерциальной системе на это тело действует сила  . Поскольку тело A в неинерциальной системе отсчёта движется равномерно и прямолинейно, то
. Поскольку тело A в неинерциальной системе отсчёта движется равномерно и прямолинейно, то  и
и  .
.
Отсюда  . Значит, кроме центробежной силы на тело, движущееся в неинерциальной системе отсчёта равномерно и прямолинейно действует ещё одна сила инерции – сила Кориолиса:
. Значит, кроме центробежной силы на тело, движущееся в неинерциальной системе отсчёта равномерно и прямолинейно действует ещё одна сила инерции – сила Кориолиса:  , которая направлена перпендикулярно направлению движения (рис. 1.3.12). Полная сила инерции в этом случае
, которая направлена перпендикулярно направлению движения (рис. 1.3.12). Полная сила инерции в этом случае  .
.
| Рисунок 1.3.11. Центробежная сила и сила Кориолиса.
|

 одинакова для всех тел, подвергшихся одинаковым по интенсивности и продолжительности воздействиям. Склонность тела сохранять параметры своего движения называется инертность. Таким образом, масса есть мера инертности тела.
одинакова для всех тел, подвергшихся одинаковым по интенсивности и продолжительности воздействиям. Склонность тела сохранять параметры своего движения называется инертность. Таким образом, масса есть мера инертности тела. . В системе СИ импульс измеряется в кг·м/с.
. В системе СИ импульс измеряется в кг·м/с. . Если записать это выражение как
. Если записать это выражение как  и назвать величину
и назвать величину  импульсом силы, то формулировка второго закона Ньютона будет: импульс силы, действующей на тело, равен изменению импульса тела.
импульсом силы, то формулировка второго закона Ньютона будет: импульс силы, действующей на тело, равен изменению импульса тела.

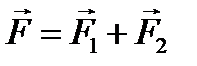


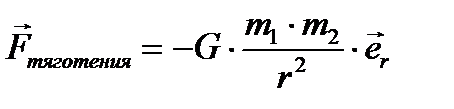


 :
: ;
; 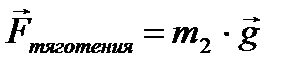
 , следовательно
, следовательно  – напряженность гравитационного поля равна ускорению, с которым будет двигаться тело массой m 2 по направлению к телу массой m 1, при условии, что других сил нет. Это ускорение называется ускорением свободного падения.
– напряженность гравитационного поля равна ускорению, с которым будет двигаться тело массой m 2 по направлению к телу массой m 1, при условии, что других сил нет. Это ускорение называется ускорением свободного падения. обычно можно считать несущественной и принимать
обычно можно считать несущественной и принимать  для всех точек пространства, описываемых в задаче. Поэтому просто записывают, что сила тяжести
для всех точек пространства, описываемых в задаче. Поэтому просто записывают, что сила тяжести 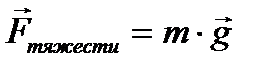
 , следовательно, на него действуют и иные силы. Как правило, это сила нормальной реакции опоры
, следовательно, на него действуют и иные силы. Как правило, это сила нормальной реакции опоры  , которая всегда перпендикулярна поверхности взаимодействия тел, или сила натяжения подвеса
, которая всегда перпендикулярна поверхности взаимодействия тел, или сила натяжения подвеса 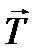 (рис. 1.3.4). Видно, что
(рис. 1.3.4). Видно, что  (рис. 1.3.4 б) и
(рис. 1.3.4 б) и  (рис. 1.3.4 г) не всегда направлены вдоль одной прямой с
(рис. 1.3.4 г) не всегда направлены вдоль одной прямой с  и не всегда равны ей по модулю.
и не всегда равны ей по модулю. – это сила, с которой тело давит на опору или натягивает подвес. Следовательно, вес приложен к опоре или подвесу, равен по модулю и противоположен по направлению силе нормальной реакции опоры (
– это сила, с которой тело давит на опору или натягивает подвес. Следовательно, вес приложен к опоре или подвесу, равен по модулю и противоположен по направлению силе нормальной реакции опоры ( ).
).







 , веса тела
, веса тела  , нормальной реакции опоры
, нормальной реакции опоры  (а, б) и натяжения подвеса
(а, б) и натяжения подвеса  (в, г).
(в, г).




 , где
, где  – все прочие силы. Когда сила сухого трения скольжения достигает максимально возможной (предельной) величины, то тела начинают двигаться друг относительно друга. Эта предельная величина рассчитывается по формуле
– все прочие силы. Когда сила сухого трения скольжения достигает максимально возможной (предельной) величины, то тела начинают двигаться друг относительно друга. Эта предельная величина рассчитывается по формуле ,
, – коэффициент трения покоя, зависящий только от природы контактирующих веществ, качества поверхностей и от температуры.
– коэффициент трения покоя, зависящий только от природы контактирующих веществ, качества поверхностей и от температуры.



 , где коэффициент трения
, где коэффициент трения  зависит только от природы контактирующих веществ, качества поверхностей и от температуры. Вообще говоря, обычно
зависит только от природы контактирующих веществ, качества поверхностей и от температуры. Вообще говоря, обычно 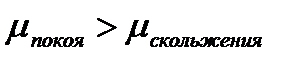 , однако в большинстве задач эти коэффициенты считаются равными.
, однако в большинстве задач эти коэффициенты считаются равными. , где коэффициент трения
, где коэффициент трения  зависит только от природы контактирующих веществ, качества поверхностей и от температуры. Обычно
зависит только от природы контактирующих веществ, качества поверхностей и от температуры. Обычно  .
.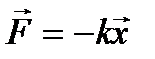 ,
, – перемещение конца стержня, то есть удлинение стержня, k – жёсткость стержня.
– перемещение конца стержня, то есть удлинение стержня, k – жёсткость стержня.

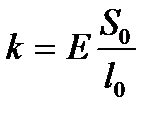
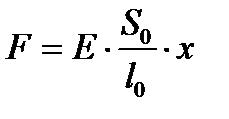 .
. называется механическим растягивающим напряжением, измеряется в Паскалях (Па),
называется механическим растягивающим напряжением, измеряется в Паскалях (Па),  . Величина
. Величина 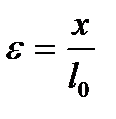 называется относительной деформацией, измеряется в долях или процентах.
называется относительной деформацией, измеряется в долях или процентах.

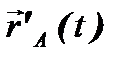


 . Поскольку это равенство выполняется всегда, то и производные по времени от обеих частей тоже равны:
. Поскольку это равенство выполняется всегда, то и производные по времени от обеих частей тоже равны:  , – или, что то же самое:
, – или, что то же самое:  .Аналогично, взяв производную от скорости по времени, получаем:
.Аналогично, взяв производную от скорости по времени, получаем:  .
. . Если штрихованная система отсчёта также является инерциальной, то и
. Если штрихованная система отсчёта также является инерциальной, то и  , а следовательно и
, а следовательно и  . То есть, система отсчёта, движущаяся относительно инерциальной поступательно без ускорения (иными словами, равномерно и прямолинейно) сама является инерциальной.
. То есть, система отсчёта, движущаяся относительно инерциальной поступательно без ускорения (иными словами, равномерно и прямолинейно) сама является инерциальной. ) и тело A движется с ускорением
) и тело A движется с ускорением  , то
, то  – ускорение инвариантно по отношению к переходу из одной инерциальной системы отсчёта в другую. Ускорения появляются при наличии силы, действующей на тело A:
– ускорение инвариантно по отношению к переходу из одной инерциальной системы отсчёта в другую. Ускорения появляются при наличии силы, действующей на тело A:  . То есть, при переходе из одной инерциальной системы отсчёта в другую силы, действующие на тела, не меняются. А следовательно, выполняется принцип относительности Галилея: все механические явления в различных инерциальных системах отсчёта протекают одинаковым образом, вследствие чего никакими механическими опытами невозможно установить, покоится ли данная система отсчёта или движется равномерно и прямолинейно. Поскольку
. То есть, при переходе из одной инерциальной системы отсчёта в другую силы, действующие на тела, не меняются. А следовательно, выполняется принцип относительности Галилея: все механические явления в различных инерциальных системах отсчёта протекают одинаковым образом, вследствие чего никакими механическими опытами невозможно установить, покоится ли данная система отсчёта или движется равномерно и прямолинейно. Поскольку  , то
, то  – преобразование Галилея.
– преобразование Галилея. ) и тело A в инерциальной системе движется с ускорением
) и тело A в инерциальной системе движется с ускорением  , то
, то  . Умножим все части уравнения на массу тела A:
. Умножим все части уравнения на массу тела A:  . Поскольку
. Поскольку  , то
, то  . Д’Аламбер предложил ввести понятие фиктивной силы инерции
. Д’Аламбер предложил ввести понятие фиктивной силы инерции  . Отличие силы инерции от реальных сил в том, что нет никакого тела, которое действует на изучаемое тело и, следовательно, в отношении силы инерции нельзя говорить о выполнимости третьего закона Ньютона. Однако понятие силы инерции очень удобно, поскольку для расчёта ускорения в неинерциальной системе отсчёта можно пользоваться формулой
. Отличие силы инерции от реальных сил в том, что нет никакого тела, которое действует на изучаемое тело и, следовательно, в отношении силы инерции нельзя говорить о выполнимости третьего закона Ньютона. Однако понятие силы инерции очень удобно, поскольку для расчёта ускорения в неинерциальной системе отсчёта можно пользоваться формулой  , понимая под
, понимая под  сумму реальных сил и силы инерции.
сумму реальных сил и силы инерции. одинаково для всех точек пространства. Если же неинерциальная система вращается, то это не так. Рассмотрим случай, когда оси z и z’ совпадают и штрихованная система вращается относительно инерциальной нештрихованной с постоянной угловой скоростью
одинаково для всех точек пространства. Если же неинерциальная система вращается, то это не так. Рассмотрим случай, когда оси z и z’ совпадают и штрихованная система вращается относительно инерциальной нештрихованной с постоянной угловой скоростью  (рис. 1.3.11). Пусть тело массой m находится в точке A, неподвижной во вращающейся (штрихованной) системе отсчёта. В этом случае радиус-вектор точки A
(рис. 1.3.11). Пусть тело массой m находится в точке A, неподвижной во вращающейся (штрихованной) системе отсчёта. В этом случае радиус-вектор точки A  , где R – расстояние от начала координат до точки А. При этом орт координаты x’
, где R – расстояние от начала координат до точки А. При этом орт координаты x’  , а орт координаты y’
, а орт координаты y’  .
.




 , а
, а  Скорость точки А:
Скорость точки А:  , а ускорение
, а ускорение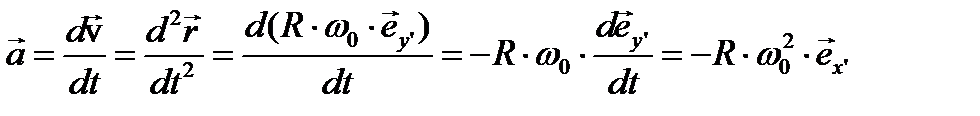 . Следовательно, в инерциальной системе на это тело действует сила
. Следовательно, в инерциальной системе на это тело действует сила  , направленная к центру вращения. Поскольку тело A в неинерциальной системе отсчёта неподвижно, то
, направленная к центру вращения. Поскольку тело A в неинерциальной системе отсчёта неподвижно, то  и
и  . Отсюда
. Отсюда  и направлена от центра вращения. Такая сила инерции называется центробежной
и направлена от центра вращения. Такая сила инерции называется центробежной 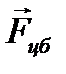 .
. ,
,  , а
, а  . Следовательно, в инерциальной системе на это тело действует сила
. Следовательно, в инерциальной системе на это тело действует сила  . Поскольку тело A в неинерциальной системе отсчёта движется равномерно и прямолинейно, то
. Поскольку тело A в неинерциальной системе отсчёта движется равномерно и прямолинейно, то  и
и  .
. . Значит, кроме центробежной силы на тело, движущееся в неинерциальной системе отсчёта равномерно и прямолинейно действует ещё одна сила инерции – сила Кориолиса:
. Значит, кроме центробежной силы на тело, движущееся в неинерциальной системе отсчёта равномерно и прямолинейно действует ещё одна сила инерции – сила Кориолиса:  , которая направлена перпендикулярно направлению движения (рис. 1.3.12). Полная сила инерции в этом случае
, которая направлена перпендикулярно направлению движения (рис. 1.3.12). Полная сила инерции в этом случае  .
.





