Найменше значення головного моменту системи сил

Для визначення найменшого значення головного моменту системи сил довільну систему сил, яка не зображена на рис. 18, послідовно зведемо до двох центрів (точок): 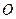– довільна точка; 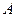– точка, яка знаходиться на центральній осі системи (рис. 18).

Позначимо відстань центра зведення 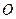до центральної осі системи через 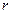, тоді (див. § 21)

.

Рис. 18

Отже,

,

.

Величина головного моменту відносно будь-якої точки зведення 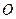і кутнахилу його до головного вектора залежить від відстані даної точки до центральної осі системи. З отриманих формул можна зробити такі висновки:

1. Для всіх центрів зведення, які знаходяться на одній і тій же відстані 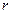від центральної осі (тобто лежать на поверхні колового циліндра, вісь якого є центральною віссю даної системи і радіус основи якого дорівнює 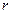), головний момент системи сил має одну і ту ж величину і утворює один і той же кут з головним вектором . Цим і пояснюється термін “центральна вісь системи”.

2. Величина головного моменту і його кут нахилу до головного вектора зростають разом із зростанням .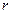

3. Головний момент має найменше значення для , тобто відносно точок центральної осі системи.

Отже, відносно точок центральної осі системи величина головного моменту має найменше значення, яке дорівнює (див. § 21) проекції головного моменту відносно довільної точки на напрям головного вектора

.

Якщо цю рівність домножити і поділити на величину головного вектора, то отримуємо формулу для обчислення найменшого значення головного моменту

,

або

.

Список
використаної літератури, деяких підручників і навчальних посібників з теоретичної механіки

1. Айзенберг Т.В., Воронков И.М., Осецкий В.М. Руководство к решению задач по теоретической механике. – М.: Высш. шк., 1961 – 390 с.

2. Айзерман М.А. Классическая механика. – М.: Наука, 1974. – 357 с.

3. Бать М.И., Джанилидзе Г.Ю., Кельзон А.С. Теоретичес-кая механика в примерах и задачах: В 3-х т. – М.: Наука, 1971. – Т.1 – 512 с.

4. Бражниченко Н.А., Кан В.Л., Минцберг Б.Л. Сборник задач по теоретической механике. – М.: Высш. шк., 1974. – 520 с.

5. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики: В 2-х т. – М.: Наука, 1970. – Т.1. – 240 с. и послед. изд.

6. Бухгольц Н.Н. Основной курс теоретической механики: В 2-х ч. – М.: Наука, 1967. – Ч.1 – 468 с.

7. Воронков И.М. Курс теоретической механики. – М.: Наука, 1966 и др. изд.

8. Гернет М.М. Курс теоретической механики. – М.: Высш. шк., 1981. – 303 с.

9. Геронимус Я.Л. Теоретическая механика. – М.: Наука, 1973. – 511 с.

10. Добронравов В.В., Никитин Н.Н., Дворников А.Л. Курс теоретической механики. – М.: Высш. шк., 1974. – 528 с.

11. Кильчевский Н.А. Курс теоретической механики:
В 2-х т. – М.: Наука, 1972. – Т.1. – 456 с; 1977. – Т.2. – 544 с.

12. Кильчевский Н.А., Ремизова Н.И., Кильчевская Е.Р. Основы теоретической механики. – К.: Вища школа, 1986. – 296 с.

13. Космодемьянский А.А. Курс теоретической механики. – М.: Учпегиз. 1965. – 655 с.

14. Лайцянский Л.Г., Лурье А.И. Курс теоретической механики: В 2-х т. – М.: Наука, 1984. – Т.1. – 352 с.

15. Маркеев А.П. Теоретическая механика. – М.: Наука, 1990. – 416 с.

16. Мещерский И.В. Сборник задач по теоретической механике. – М.: Наука, 1981. – 480 с. и др. изд.

17. Павловский М.А., Путята Т.В. Теоретическая механика. – К.: Вища школа, Головне вид-во. 1985. – 327 с.

18. Павловський М.А., Акінфієва Л.Ю., Юрокін А.І., Свистунов С.Я. Кінематика та динаміка точки. Комп’ютерний курс. – К.: Либідь, 1993. – 248 с.

19. Савин Г.Н., Кильчевский Н.А., Путята Т.В. Теоретическая механика. – Л.: Изд. техн. лит., 1963. – 610 с.

20. Савин Г.Н., Путята Т.В., Фрадлин Б.Н. Курс теоретической механики. – К.: Вища шк., 1973. – 359 с.

21. Сборник заданий для курсовых работ по теоретической механике / Под ред. проф. А.А.Яблонского. – М.: Высш. шк., 1972. – 432 с.

22. Сборник задач по теоретической механике / Под ред. Колесникова К.С. – М.: Наука, 1989. – 448 с.

23. Старжинский В.М. Теоретическая механика. – М.: Наука, 1980. – 464 с.

24. Тарг С.М. Краткий курс теоретической механики. – М.: Наука, 1986. – 478 с.

25. Яблонский А.А. Курс теоретической механики:
В 2-х т. – М.: Высш. шк., 1977. – Т.1. – 431 с.