 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Центр ваги дуги кола
|
|
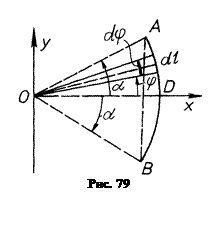
Розглянемо дугу ADВ кола радіуса R з центральним кутом  . Помістимо початок системи координат в центрі кола, а вісь Ох проведемо як вісь симетрії дуги (рис. 79). Оскільки вісь Ох є віссю симетрії дуги, то центр ваги її буде знаходитись на цій осі, тобто
. Помістимо початок системи координат в центрі кола, а вісь Ох проведемо як вісь симетрії дуги (рис. 79). Оскільки вісь Ох є віссю симетрії дуги, то центр ваги її буде знаходитись на цій осі, тобто 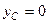 , і залишається знайти тільки
, і залишається знайти тільки  . Для цього скористаємося формулою
. Для цього скористаємося формулою
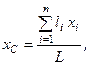
в якій сумування замінимо інтегруванням, тобто
 (а)
(а)
В даній формулі  – довжина дуги, яка вираховується за формулою
– довжина дуги, яка вираховується за формулою
 (б)
(б)
Щоб вирахувати інтеграл, який стоїть в чисельнику, під кутом 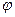 виділимо елемент дуги
виділимо елемент дуги  , центральний кут якої
, центральний кут якої  , тоді
, тоді  . Координата
. Координата  виділеного елемента дуги, згідно з рис. 79 визначиться за формулою
виділеного елемента дуги, згідно з рис. 79 визначиться за формулою

Тоді
 (в)
(в)
Підставляючи (б) і (в) в (а), отримаємо
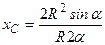 ,
,
або
 (1.77)
(1.77)
Отримана формула визначає центр ваги дуги радіуса  . В даній формулі
. В даній формулі 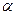 – половина центрального кута дуги в радіанах.
– половина центрального кута дуги в радіанах.
В частковому випадку для дуги півкола  будемо мати
будемо мати
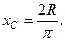 (1.78)
(1.78)
Центр ваги площі кругового сектора
 Для визначення центра ваги сектора круга радіуса
Для визначення центра ваги сектора круга радіуса  з центральним кутом
з центральним кутом  розіб’ємо його на елементарні сектори, як показано на рис. 80. Кожний з цих елементарних секторів можна розглядати як трикутник, адже дугу, якою обмежений цей сектор, через її малість можна розглядати як прямолінійний відрізок. Центр ваги такого трикутника знаходиться в точці перетину його медіан, тобто на відстані
розіб’ємо його на елементарні сектори, як показано на рис. 80. Кожний з цих елементарних секторів можна розглядати як трикутник, адже дугу, якою обмежений цей сектор, через її малість можна розглядати як прямолінійний відрізок. Центр ваги такого трикутника знаходиться в точці перетину його медіан, тобто на відстані  від вершини. Отже, геометричним місцем центрів ваг всіх елементарних секторів є дуга
від вершини. Отже, геометричним місцем центрів ваг всіх елементарних секторів є дуга  кола радіуса
кола радіуса  . Знай-шовши центр ваги цієї дуги, тим самим знайдемо центр ваги площі кругового сектора. Застосовуючи формулу (1.77), отримаємо
. Знай-шовши центр ваги цієї дуги, тим самим знайдемо центр ваги площі кругового сектора. Застосовуючи формулу (1.77), отримаємо
 (1.79)
(1.79)
Отримана формула визначає центр ваги площі сектора круга радіуса  . В цій формулі
. В цій формулі 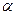 – половина центрального кута в радіанах. В частковому випадку, для півкруга
– половина центрального кута в радіанах. В частковому випадку, для півкруга  отримаємо
отримаємо
 (1.80)
(1.80)
Формули для визначення положення центра ваги інших геометричних фігур можна знайти в різних технічних довідниках.
§ 34 Способи визначення положення центра ваги тіла
Центр ваги твердого тіла можна визначити як експериментально, так і аналітично, тобто проведенням відповідних розрахунків.
Найпростішим експериментальним способом визначення положення центра ваги тіла є:
Спосіб підвішування
Цей спосіб полягає в тому, що тіло послідовно підвішують за дві які-небудь його точки (рис. 81). Оскільки на підвішене тіло діють тільки дві сили (натяг нитки і сила ваги тіла), то в положенні рівноваги ці сили діють по одній прямій в протилежні боки. Отже, центр ваги тіла буде знаходитись на лінії, що є продовженням нитки: якщо тіло підвішено за точку А – то на лінії АА 1 (рис. 81, а), якщо за точку В – то на лінії ВВ 1 (рис. 81, б). Точка С перетину цих ліній буде центром ваги тіла.

Рис. 81
Спосіб зважування
Для визначення положення центра ваги деякого тіла в точках А, В і D кладемо його на платформи трьох ваг (рис. 82). Тіло перебуває в рівновазі під дією чотирьох сил: 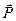 – сила ваги тіла;
– сила ваги тіла;  – реакції платформ, величини яких вкажуть відповідні ваги. Ці сили утворюють систему паралельних сил. Складемо рівняння рівноваги
– реакції платформ, величини яких вкажуть відповідні ваги. Ці сили утворюють систему паралельних сил. Складемо рівняння рівноваги

Рис. 82

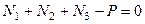 ;
;

 ;
;

 .
.
З першого рівняння знаходимо вагу тіла
 .
.
З другого рівняння визначаємо ординату центра ваги

З третього рівняння знаходимо абсцису центра ваги

Координати  легко визначаються експериментально.
легко визначаються експериментально.
Координату  об’ємного тіла визначимо, якщо тіло повернемо на кут 90° навколо горизонтальної осі і зробимо повторне зважування.
об’ємного тіла визначимо, якщо тіло повернемо на кут 90° навколо горизонтальної осі і зробимо повторне зважування.
Серед аналітичних методів визначення положення центра ваги виділимо:
Спосіб розбиття
Для визначення положення центра ваги тіл складної геометричної форми їх уявно розбивають на частини, центри ваг яких відомі, і за загальними формулами (1.69-1.75) обчислюють координати центра всього тіла. Наприклад, треба визначити координати центра ваги плоскої фігури, що зображена на рис. 83, а. Задану фігуру можна розбити на три прямокутники, площі  ,
,  ,
,  та координати центрів ваг
та координати центрів ваг  ,
,  ,
,  яких при заданні відповідних розмірів легко визначаються. Координати
яких при заданні відповідних розмірів легко визначаються. Координати  ваги площі всієї фігури знаходять за формулами
ваги площі всієї фігури знаходять за формулами



Рис. 83
Спосіб від’ємних ваг (площ)
Цей спосіб застосовується для знаходження координат центра ваги тіл, які мають вирізи (пустоти). Розглянемо плоске тіло, що має дві пустоти (рис. 83, б). Позначимо  – вагу тіла, яке має пустоти,
– вагу тіла, яке має пустоти,  ,
,  – координати його центра ваги;
– координати його центра ваги;  і
і  – ваги речовин, які вибрані з пустот 1 і 2;
– ваги речовин, які вибрані з пустот 1 і 2;  ;
;  – координати центрів ваг пустот;
– координати центрів ваг пустот; 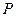 – вага тіла разом з вагою пустот, тобто
– вага тіла разом з вагою пустот, тобто 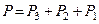 ;
;  – координати центра ваги тіла, яке не має пустот. Ці координати, очевидно, можна визначити за формулами
– координати центра ваги тіла, яке не має пустот. Ці координати, очевидно, можна визначити за формулами
 (а)
(а)
Оскільки  , а
, а 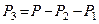 , то з формули (а) знаходимо координати центра ваги тіла, що має пустоти
, то з формули (а) знаходимо координати центра ваги тіла, що має пустоти
 ,
,
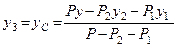 .
.
З отриманих формул можна зробити такий висновок:
для визначення координат центра ваги тіла, що має вирізи (пустоти), можна використати метод розбиття на такі частини: все тіло разом з пустота-ми та пустоти, але вважати, що пустоти мають від’ємну вагу (для плоского тіла – від’ємну площу).
Питання для самоконтролю
1. Яка система сил називається паралельною?
2. До якого канонічного вигляду можна звести систему паралельних сил?
3. Що називається центром паралельних сил?
4. За якими формулами визначаються координати центра паралельних сил?
5. Що називається вагою тіла?
6. Запишіть найбільш загальні формули, які визначають координати центра ваги тіла.
7. За якими формулами визначаються координати центра ваги однорідного тіла?
8. Запишіть формули, які визначають координати центра ваги однорідного плоского тіла.
9. Запишіть формули, які визначають статичні моменти плоскої фігури відносно осей абсцис і ординат.
10. Тіло має елемент симетрії. Де знаходиться його центр ваги?
11. Де знаходиться центр ваги площі трикутника? За якими формулами можна вирахувати координати центра ваги трикутника?
12. За якою формулою обчислюється координата центра ваги дуги кола?
13. За якою формулою обчислюється координата центра ваги площі кругового сектора?
14. Які є експериментальні способи визначення положення центра ваги тіла? Поясніть їх сутність.
15. Які є аналітичні методи визначення координат центра ваги тіла? Поясніть їх сутність.
2 КІНЕМАТИКА
§ 35 Предмет кінематики
Кінематика – це розділ теоретичної механіки, в якому вивчається механічний рух матеріальних об’єктів незалежно від сил, які викликають або змінюють цей рух.
Іншими словами, в кінематиці вивчається переміщення матеріальних об’єктів в просторі і в часі без врахування їх матеріальної структури і взаємодії їх з іншими матеріальними системами. А тому матеріальну точку в кінематиці просто називають точкою, а саму кінематику називають геометрією руху.
Основними завданнями теоретичного курсу кінематики є отримання формул (рівнянь), які визначають кінематичні характеристики механічного руху матеріальних об’єктів. Основними кінематичними характеристиками руху твердого тіла є закон руху, кутова швидкість, кутове пришвидшення, швидкість і пришвидшення точки, яку вибирають за полюс, і т. ін. Кінематичними характеристиками руху точки є закон (рівняння) руху, траєкторія руху, швидкість і пришвидшення точки.
1. Рівняння (закон руху) – математичні рівняння, за допомогою яких можна визначити положення матеріального об’єкта в будь-який момент часу.
2. Траєкторія – це геометричне місце послідовних положень точки в просторі.
З визначення випливає, що поняття траєкторії існує тільки для точки, і тому дана кінематична характеристика визначається або задається тільки в тому випадку, коли вивчається рух точки.
3. Швидкість точки – векторна величина, що характеризує в кожний момент часу бистроту і напрям зміни руху точки в заданій системі відліку.
4. Пришвидшення точки – векторна величина, що характеризує в кожний момент часу бистроту зміни вектора швидкості за величиною і напрямом в заданій системі відліку.
5. Кутова швидкість – в загальному випадку векторна величина, яка характеризує в кожний момент часу бистроту і напрям зміни обертання тіла в заданій системі відліку.
6. Кутове пришвидшення – в загальному випадку векторна величина, яка характеризує в кожний момент часу бистроту і напрям зміни вектора кутової швидкості тіла в заданій системі відліку.
Якщо для певного руху матеріального об’єкта отримані формули, за допомогою яких визначені перераховані кінематичні характеристики, то можна вважати, що основне завдання теоретичного курсу кінематики розв’язане.
Основним завданням практичної частини курсу кінематики є визначення за допомогою формул, отриманих в теоретичному курсі, кінематичних характеристик руху окремих точок матеріального об’єкта. Треба зазначити, що визначені кінематичні характеристики руху, як і сам механічний рух, є відносними. Їх величина і характер зміни залежать від вибору системи відліку. Так, наприклад, траєкторія руху будь-якої точки обода колеса автомобіля, який рухається по дорозі відносно автомобіля, буде коло, а відносно дороги (землі) – циклоїда. А тому при визначенні кінематичних характеристик руху необхідно чітко з’ясувати, в якій системі відліку вони визначаються. В кінематиці систему відліку найчастіше пов’язу-ють з Землею, а останню вважають нерухомою.
Кінематику можна назвати геометричним вченням про рух, бо вона питання про сили, які зумовлюють цей рух, зовсім не розглядає. Ширша постановка питання про рух тіл, де на перший план висувається зв’язок між рухом тіла і прикладеними до нього силами, належить динаміці, а тому кінематику часто трактують як вступ до динаміки. Але треба мати на увазі, що результати встановлені в кінематиці, мають і велике самостійне значення. Для багатьох механізмів питання про діючі сили має порівняно другорядне значення. Правильна ж дія механізму забезпечується досконалим кінематичним аналізом рухів окремих його частин (ланок).
Основними матеріальними об’єктами, механічний рух яких вивчається в кінематиці, є точка і тверде тіло. А тому саму кінематику можна розділити на кінематику точки і кінематику твердого тіла.
2.1 Кінематика точки
Рух точки як об’єкта, розмірами якого нехтують, можна розглядати як простий або складний. Простий рух і відносний у випадку складного руху точки можна задати і вивчити трьома способами: векторним, координатним і натуральним.
§ 36 Векторний спосіб вивчення руху точки
В даному способі положення рухомої точки 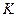 визначається вектором
визначається вектором  , початок якого знаходиться в деякому нерухомому центрі
, початок якого знаходиться в деякому нерухомому центрі 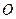 . Цей вектор позначається буквою
. Цей вектор позначається буквою 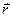 і називається радіусом-вектором рухомої точки
і називається радіусом-вектором рухомої точки 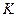 . При русі точки радіус-вектор
. При русі точки радіус-вектор 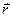 неперервно змінюється як за напрямом, так і за величною. Наприклад, в момент
неперервно змінюється як за напрямом, так і за величною. Наприклад, в момент  рухома точка займає положення
рухома точка займає положення 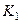 , а її радіус-вектор
, а її радіус-вектор 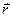 приймає значення
приймає значення 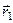 . Отже,
. Отже, 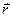 є функцією часу
є функцією часу 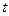 . Математично це можна описати так:
. Математично це можна описати так:
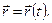 (2.1)
(2.1)
Рівняння (2.1) є рівнянням (законом) руху точки у векторній формі. Для визначення траєкторії точки згадаємо одне визначення з математики:
лінія, яка описується в просторі кінцем змінного вектора, початок якого знаходиться в нерухомій точці, називається годографом даного вектора.
Отже, у відповідності з рис. 84 траєкторією руху точки при векторному способі задання її руху є годограф її радіуса-вектора 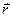 .
.
Для визначення швидкості точки розглянемо два її послідовні положення. Припустимо, що в момент часу 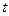 рухома точка перебуває в положенні
рухома точка перебуває в положенні 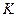 , яке визначається радіусом-вектором
, яке визначається радіусом-вектором 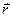 , а в момент
, а в момент  – в положенні
– в положенні 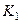 , яке визначається радіусом-вектором
, яке визначається радіусом-вектором  (рис. 85).
(рис. 85).
Отже, за проміжок часу  точка змістилася на вектор
точка змістилася на вектор  . Відношення приросту
. Відношення приросту 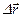 радіуса-вектора точки до приросту часу
радіуса-вектора точки до приросту часу  називається середньою швидкістю точки за проміжок часу
називається середньою швидкістю точки за проміжок часу  , тобто
, тобто

 .
.
Вектор середньої швидкості напрямлений по вектору 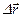 , тобто по хорді
, тобто по хорді  .
.
 Рис. 84
Рис. 84
|  Рис. 85
Рис. 85
|
Швидкість точки в даний момент, або просто швидкість точки, – це граничне значення середньої швидкості, коли приріст часу  прямує до нуля, тобто:
прямує до нуля, тобто:

 . (а)
. (а)
Згідно з рівнянням (2.1) 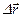 є неперервною функцією часу
є неперервною функцією часу 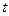 , а це означає, що границя цього відношення є похідна від
, а це означає, що границя цього відношення є похідна від 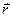 за часом
за часом 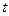 .
.
Отже,
 . (2.2)
. (2.2)
Швидкість точки дорівнює першій похідній за часом від її радіуса-вектора.
Зауваження. Похідні за часом в механіці прийнято позначити крапочками зверху, тобто: 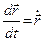 ;
;  і т.д.
і т.д.
З отриманої формули видно:
1) швидкість точки – це вектор, про що було сказано вище;
2) вектор швидкості точки напрямлений по дотичній до її траєкторії в бік її руху, бо граничне положення вектора 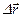 , коли
, коли  , є положення дотичної до годографа вектора
, є положення дотичної до годографа вектора  (рис. 85).
(рис. 85).
 Для визначення пришвидшення точки знову розглянемо два її послідовні положення. Нехай в момент часу
Для визначення пришвидшення точки знову розглянемо два її послідовні положення. Нехай в момент часу 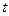 рухома точка перебуває в положенні
рухома точка перебуває в положенні 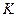 і має швидкість
і має швидкість 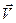 , а в момент
, а в момент  – в положенні
– в положенні 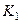 , де її швидкість
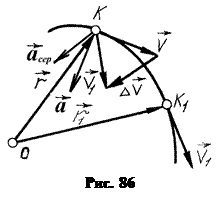
, де її швидкість 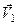 (рис. 86). Отже, за проміжок часу
(рис. 86). Отже, за проміжок часу  вектор швидкості точки отримав приріст
вектор швидкості точки отримав приріст  . Цей приріст знайдемо, якщо вектор
. Цей приріст знайдемо, якщо вектор 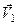 умовно перенесемо в точку
умовно перенесемо в точку 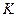 і з’єднаємо кінці векторів
і з’єднаємо кінці векторів 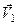 і
і 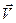 (рис. 86).
(рис. 86).
Відношення приросту  вектора швидкості точки до приросту часу
вектора швидкості точки до приросту часу  називається середнім пришвидшенням точки за проміжок часу
називається середнім пришвидшенням точки за проміжок часу  , тобто:
, тобто:

Вектор середнього пришвидшення напрямляється по вектору  (рис. 86).
(рис. 86).
Пришвидшення точки в даний момент часу, або просто пришвидшення точки, – це є граничне значення середнього пришвидшення коли приріст часу  прямує до нуля, тобто:
прямує до нуля, тобто:


Отже
 (2.3)
(2.3)
Пришвидшення точки дорівнює першій похідній за часом від вектора її швидкості.
Якщо врахувати формулу (2.2) для швидкості, то отримаємо
 (2.3)
(2.3)
Пришвидшення точки дорівнює другій похідній за часом від її радіуса-вектора.
З отриманих формул випливає:
1. Пришвидшення точки – це вектор.
 2. Вектор пришвидшення точки напрямлений в бік вгнутості її траєкторії і лежить в стичній площині (рис. 86).
2. Вектор пришвидшення точки напрямлений в бік вгнутості її траєкторії і лежить в стичній площині (рис. 86).
3. Вектор пришвидшення точки напрямлений по дотичній до годографа вектора її швидкості. І дійсно, якщо побудувати годограф вектора швидкості (рис. 87), то вектор  – це хорда
– це хорда  , граничне положення якої, коли
, граничне положення якої, коли  , є дотична.
, є дотична.
§ 37 Координатний спосіб вивчення руху точки
 В даному способі положення рухомої точки в просторі визначається координатами. Значення цих координат суттєво залежить від вибраної системи координат: декартова, циліндрична, сферична і т.д. В механіці, як і в математиці, найчастіше використовують декартову систему координат, в якій положення рухомої точки
В даному способі положення рухомої точки в просторі визначається координатами. Значення цих координат суттєво залежить від вибраної системи координат: декартова, циліндрична, сферична і т.д. В механіці, як і в математиці, найчастіше використовують декартову систему координат, в якій положення рухомої точки 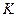 в просторі визначається координатами
в просторі визначається координатами  (рис. 88). При русі точки ці координати змінюються, тобто є деякими функціями часу
(рис. 88). При русі точки ці координати змінюються, тобто є деякими функціями часу
 (2.5)
(2.5)
Рішення (2.5) називаються кінематичними рівняннями руху точок в декартовій системі координат. Передбачається, що функції  ,
,  і
і  є однозначними, неперервними і принаймні два рази неперервно диференційованими.
є однозначними, неперервними і принаймні два рази неперервно диференційованими.
Легко встановити зв’язок між векторним і координатним способами задання руху точки. З рис. 88 видно, що
 , (2.6)
, (2.6)
де 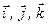 – орти відповідних осей координат.
– орти відповідних осей координат.
З математичної точки зору рівняння (2.5) – це параметричні рівняння лінії в просторі. Очевидно, цією лінією є траєкторія рухомої точки. Отже, рівняння (2.5) є також рівняннями траєкторії точки в параметричній формі. Виключивши з рівнянь (2.5) параметр 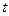 , отримаємо рівняння траєкторії в явній формі. Виключення можна провести за такою схемою. З першого рівняння системи (2.5) знаходимо
, отримаємо рівняння траєкторії в явній формі. Виключення можна провести за такою схемою. З першого рівняння системи (2.5) знаходимо 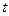 як функцію
як функцію 
 ,
,
і цей вираз підставляємо в друге і третє рівняння. Тоді отримаємо
 (2.7)
(2.7)
Отримані результати є рівняннями траєкторії точки в декартових координатах. Треба зазначити, що тут приведено лише схему виключення параметрів 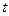 . На практиці залежно від заданих рівнянь, наших знань і умінь застосовують різноманітні способи виключення параметра
. На практиці залежно від заданих рівнянь, наших знань і умінь застосовують різноманітні способи виключення параметра 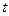 .
.
Приклад. Знайти рівняння траєкторії точки, рух якої описується рівняннями
 ,
, 
Розв’язання. Знаючи, що  , виключення параметра
, виключення параметра 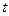 проводимо так:
проводимо так:



Це є рівняння еліпса. Отже, траєкторія точки є еліпс, а виключення параметра 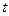 проведено за допомогою тригонометричної тотожності.
проведено за допомогою тригонометричної тотожності.
Для отримання формул, за допомогою яких визначається швидкість точки, коли рух її задано координатним способом, тобто задані рівняння (2.5), використаємо формули (2.2) і (2.6). Підставивши (2.6) в (2.2), отримаємо

Оскільки 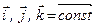 , то маємо
, то маємо

Звідси, згідно з основними положеннями векторної алгебри отримаємо, що проекції вектора швидкості на декартові осі координат будуть визначатись за формулами
 (2.8)
(2.8)
тобто:
проекції вектора швидкості на декартові осі координат дорівнюють першим похідним за часом від відповідних координат.
За отриманими проекціями визначаємо величину вектора швидкості
 (2.9)
(2.9)
і його напрямні косинуси


 (2.10)
(2.10)
Отримані формули (2.8)-(2.10) визначають вектор швидкості точки у випадку, коли рух її задано в декартовій системі координат, тобто задані рівняння (2.5).
Використовуючи формули (2.4) і залежність (2.6), отримаємо формули для визначення пришвидшення. Підставляючи (2.6) в (2.4), отримаємо

або


Звідси, згідно з основними положеннями векторної алгебри проекції вектора пришвидшення на декартові осі координат будуть визначатись формулами


 (2.11)
(2.11)
тобто:
проекції вектора пришвидшення на декартові осі координат дорівнюють другим похідним за часом від відповідних координат.
Знаючи проекції, за формулою
 (2.12)
(2.12)
вираховуємо величину вектора пришвидшення, а його напрямні косинуси – за формулами



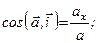

 (2.13)
(2.13)
Формули (2.11)-(2.13) визначають вектор пришвидшення точки у випадку, коли рух її задано в декартовій системі координат, тобто задано рівняннями (2.5).
§ 38 Швидкість і пришвидшення точки
в полярних координатах
 Як практичне застосування отриманих формул, визначи-мо швидкість і пришвидшення точки в полярних координатах. З математики відомо, що положення точки на площині можна визначити параметрами
Як практичне застосування отриманих формул, визначи-мо швидкість і пришвидшення точки в полярних координатах. З математики відомо, що положення точки на площині можна визначити параметрами 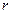 і
і 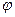 , які є координатами полярної системи координат (рис. 89). На цьому рисунку для наочності зображено і декартову систему координат
, які є координатами полярної системи координат (рис. 89). На цьому рисунку для наочності зображено і декартову систему координат 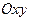 . При русі точки координати
. При русі точки координати 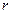 і
і 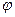 неперервно змінюються, тобто є функціями часу
неперервно змінюються, тобто є функціями часу 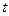

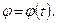 (2.14)
(2.14)
Записані рівняння є рівняннями руху точки в полярних координатах. З рис. 89 видно, що залежність між декартовими і полярними координатами визначається співвідношеннями
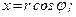
 (а)
(а)
Продиференціювавши співвідношення (а) за часом, отримаємо проекції вектора швидкості точки на декартові осі координат
 (б)
(б)
і, використовуючи формулу (2.9), визначимо величину вектора швидкості

Отже,
 (2.15)
(2.15)
 Формула (2.15) визначає величину швидкості точки, рух якої задано в полярних координатах, тобто визначається рівняннями (2.14). Введемо одиничні вектори полярної системи координат:
Формула (2.15) визначає величину швидкості точки, рух якої задано в полярних координатах, тобто визначається рівняннями (2.14). Введемо одиничні вектори полярної системи координат:  напрямлений по радіусу-вектору
напрямлений по радіусу-вектору 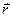 в бік зростання
в бік зростання 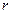 і
і  , повернутий відносно
, повернутий відносно  на кут
на кут 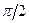 в бік зростання кута
в бік зростання кута 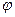 (рис. 89). Із формули (2.15) видно, що швидкість точки в полярній системі координат дорівнює сумі двох взаємно перпендикулярних векторів:
(рис. 89). Із формули (2.15) видно, що швидкість точки в полярній системі координат дорівнює сумі двох взаємно перпендикулярних векторів:  – радіальної складової і
– радіальної складової і  – поперечної (трансверсальної) складової. Якщо
– поперечної (трансверсальної) складової. Якщо  і
і  додатних знаків, то вектори
додатних знаків, то вектори 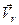 і
і  співпадають із напрямами одиничних векторів
співпадають із напрямами одиничних векторів  і
і  і навпаки, якщо
і навпаки, якщо 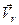 і
і  від’ємних знаків, то і вектори
від’ємних знаків, то і вектори 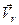 і
і  мають напрями, протилежні до
мають напрями, протилежні до  і
і  (рис. 90).
(рис. 90).
За допомогою формул (2.11) і (2.12) визначимо пришвидшення точки. Для цього співвідношення (б) ще раз диференціюємо за часом

Згрупувавши окремі члени, отримаємо

Величину вектора пришвидшення визначимо за формулою
 . (2.16)
. (2.16)
Формула (2.16) визначає величину вектора пришвидшення точки, рух якої задано в полярних координатах, тобто визначається рівняннями (2.14).
Із формули (2.16) видно, що пришвидшення точки в полярній системі координат дорівнює сумі двох взаємно перпен-дикулярних векторів:  – радіальної складової і
– радіальної складової і  – трансверсальної складової. Напрями векторів
– трансверсальної складової. Напрями векторів 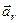 і
і  визначаються так само, як і напрями векторів швидкості, і залежать від знаків алгебраїчних величин
визначаються так само, як і напрями векторів швидкості, і залежать від знаків алгебраїчних величин  і
і  . Вектори
. Вектори 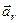 і
і  для випадку
для випадку  і
і  показані на рис. 90.
показані на рис. 90.
Дата публикования: 2014-11-04; Прочитано: 4255 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
